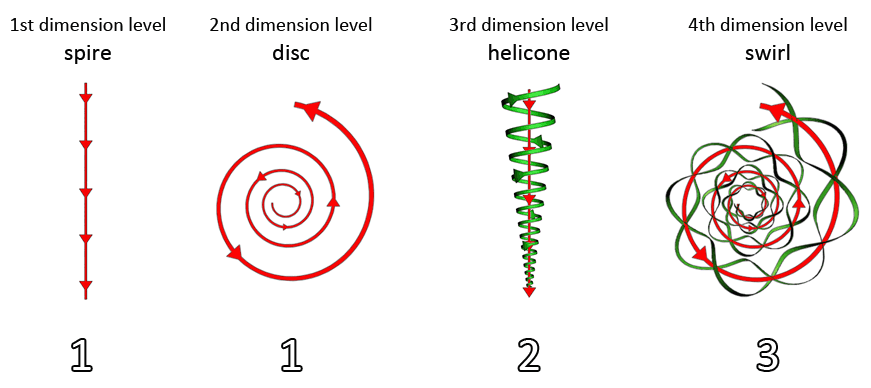
Meridians

Growth Rate of Meridians

When the number of meridians for a vortex grows, like when the vortex is morphing upwards, it does not do so in steps. The numbers do not instantly grow from 1 to 2 or from 2 to 3. A vortex can also own a meridian that is only half grown, thus half a meridian. The number of meridians grow gradually from 1 to 2 and 2 to 3 as the vortex morphs upwards.

And this growth also does not occur linearly. A simple way we can predict that the growth of this number is not linear is because in that case the growth ratio for the meridians of a vortex would decrease with each dimension level, and thus a vortex that is very high dimensional, with a high number of meridians, would then increase only with a low number of meridians when morphing to the next high level. Such a vortex would look nearly the same as the previous vortex, but we know that this is not so. Every next vortex in the sequence looks different to its previous vortex.

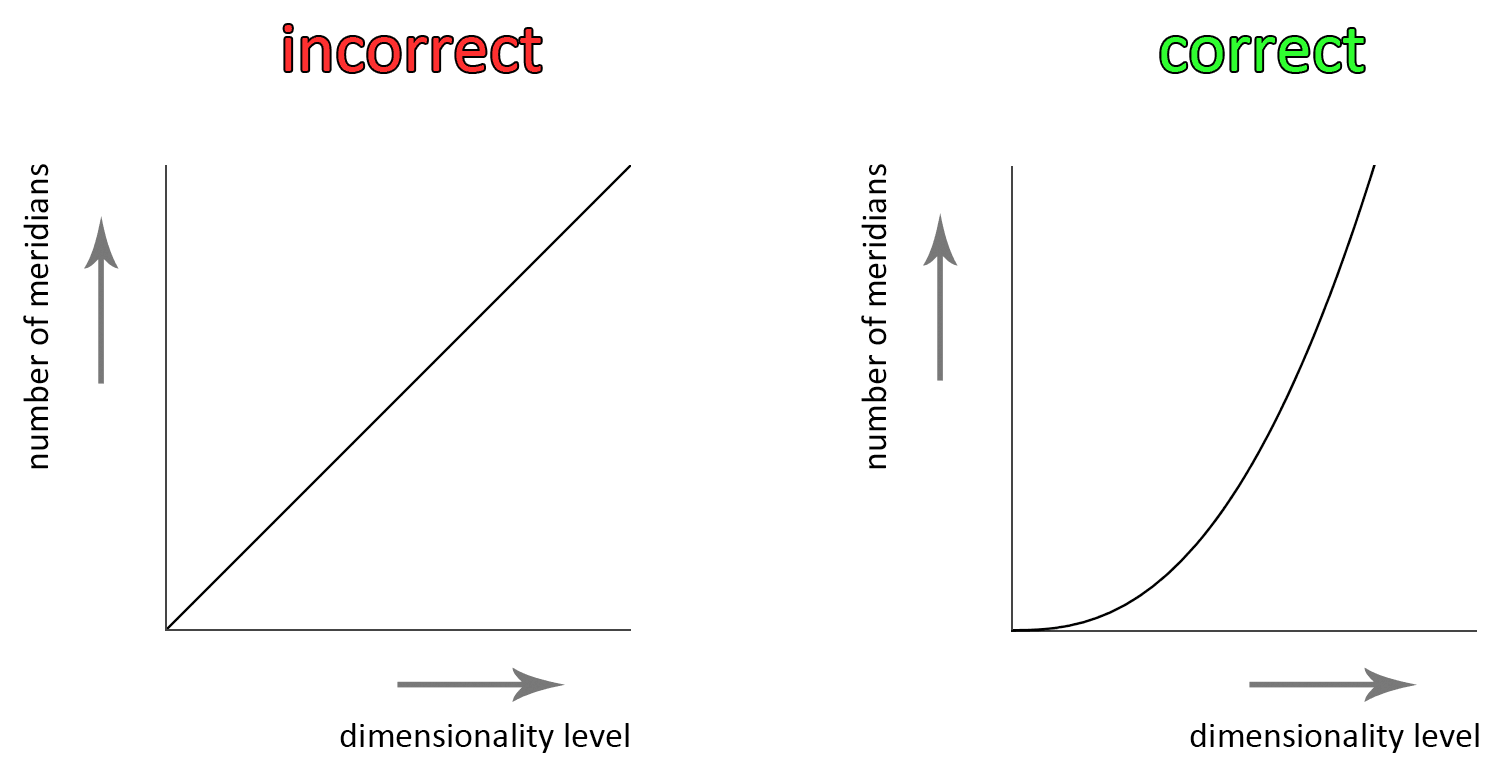
The number of meridians should increase at an exponential rate. This is a logical scenario because then the number of meridians for a vortex that has a high number of meridians increases with a large number. The increase with a significant percentage of new meridians is required for a vortex to take on a new shape. It is likely that this increase in numbers can be plotted with an equation. But the correct math for this equation is unknown at this point, uncertain, because we can only see the sum movement of a vortex, not the individual movements. There is however one direction to look for that might provide some valuable answers to this missing equation.

Fibonacci numbers

One direction to look for when trying to determine at what rate, and with what equation the number of meridians increases with the increase of the dimensionality levels might be the following sequence of numbers. It is called the Fibonacci sequence.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, ...
 

The first two numbers in the Fibonacci sequence are 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence. Then each number that follows is the sum of the previous two numbers. The sequence does not have an end value, it can contain an infinite amount of numbers.

The Fibonacci sequence is named after Fibonacci (Leonardo Bonacci), who lived from 1170 to 1250. He was an Italian mathematician, best known to the modern world for spreading of the Hindu–Arabic numeral system in Europe. He did not discover the Fibonacci sequence but used it as an example in the Liber Abaci, a historic book on arithmetic (oldest branch of mathematics).

This Fibonacci sequence seems to appear everywhere in nature. From the growth of of the buds on trees to the number of petals on flowers. If you search for it on the internet then you'll find plenty of websites and a great diversity of examples. Some people seem to be quite fascinated with this mysterious number sequence. There is an apparent link with this number sequence and the number of meridians in the transformation sequence which I will attempt to explain. To do that, I need you to look at a few different growth patterns in plants. We start with a flower.
 

Image by Alvesgaspar (Wikimedia), under CC BY-SA 3.0 license. Both images were cropped.
Right image spirals added by different author.

The above image shows a Yellow Chamomile flower. If you look carefully at the flower head you might notice a spiral pattern which at first glance appears to go in one direction. If you keep looking then a little later you see another spiral pattern going in the other direction. It almost looks like the plant is a vortex, with a left and a right turning movement. It looks like a vortex that is frozen in time.

There are 21 left turning lines (blue) in the second image on the right, and 13 right turning lines (aqua). These two numbers, 21 and 13, are both Fibonacci numbers. The two are subsequent numbers in the sequence.

At this point we might think that perhaps these left and right turning movements of the flower head are the left and right turning movements (meridians) of a vortex. But this flower alone doesn't clarify that. So far we do not know if the shape of the flower is influenced by the shape of a vortex. If we look at the spiral patterns on a conifer cone, on the images below, then we see the same kind of pattern that we saw in the flower head. This time with 13 left-turning movements (blue) and 8 right-turning movements (red). By looking at the zigzag patterns that we see on the side of the cone (left image) we should sense that there's a high probability that the shape of this cone is related to vortex movement, and the zigzag pattern is a result of the left and right turning movements that are braided.
 

Image by Didier Descouens (Wikimedia), under CC BY-SA 3.0 license

Image by Donald Collins

There are ways in which we can determine if the growth of the number of meridians in the transformation sequence matches the progression of the Fibonacci sequence. What we need to do is look at every subsequent vortex in the sequence and try to determine the minimum number of movements required to make such a vortex. The spire is only a single movement in a straight line. So the most probable number of meridians is one. The disc is also just one movement, one that is bend. The number here should again be one. The helicone has thickness, and rotates along its axis. The axis is the core movement, the visible helix movement is the peripheral movement. The number of meridians here is two. The swirl rotates around its center, like the disc does, but it does not rotate along its length axis. So here we might think that all meridians go in the same direction. But that would make all the peripheral movements same as a core movement. And core movements alone are not visible or tangible. We know that the swirl can create visible and tangible matter. A more logical thought is that there are movements rotating around the core, like the helicone demonstrated to us. This rotation around the core line could be the reason why the helicone and the swirl can produce tangible matter. The explanation for why we can not see this rotation could be that there are at least two movements, going both in opposite direction. The sum movement of both these movements cancels out the visible rotation around the length axis, and result into one single movement in the same direction as the length axis. Thus here, the minimum number of movements (meridians) is three.

For the first 4 vortices of the first cycle, the numbers match the numbers of the Fibonacci sequence. But we do not know if the numbers match for all the vortices that come after the swirl. Those vortices are more complex and we cannot give a quick estimation of the number of movements in those vortices merely by looking at their shape. So at this point we are again not certain. You should also keep in mind that the number of meridians we are trying to determine here are the minimum number of meridians per vortex. The minimum required number for the vortex to be able to fully form its shape. The number of meridians can for any vortex be higher than that number, due to upmorphing or due to more meridians being present within the medium in which the vortex appears.
 

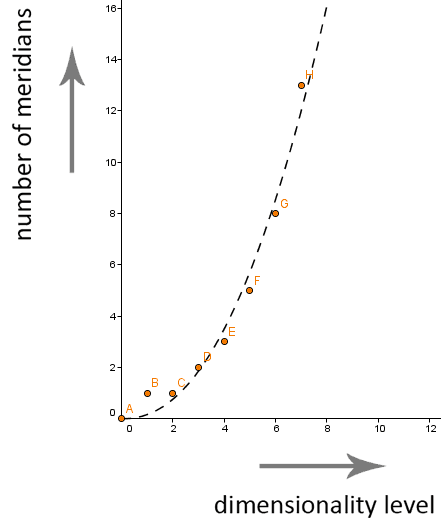
The Fibonacci sequence is one possible series of numbers that might explain how the number of meridians increase for each added level of dimensionality of a vortex. It is one possible way how the sequence might grow in an exponential rate. But it is not certain that this is the correct rate in which that happens. Still, because of the many indications that the Fibonacci sequence can be found in all sorts of visual patterns found in nature, and because there are some clues that possibly link this sequence of numbers to vortex movement, I do believe there's a good chance that there's a clear link between the number of meridians and the Fibonacci sequence.

If you browse through the pages of the ladders and the spirals, you might notice that the number of meridians for some vortices are indicated as an estimated number. The source of that number is the Fibonacci sequence. I allowed myself to make an estimation based on these numbers.

Angularity

Before my work on the  infinity-theory I knew from the yin/yang theory that angularity is a form of yangness, a form of low dimensionality. But I knew little more than that. I did not knew in what way an angular shape is more yang, or for what reason an angular shape is more yang. For example, of all the grains and grain-like seeds that can be eaten, buckwheat is among the most yang. The shape of a buckwheat seed is also the most angular.

A movement in a straight line is the most simple movement we can imagine. A curved line is more complex, and requires more freedom of movement to make. This freedom of movement is more and more abundant in the higher dimensions.

One way that we can learn about the relation between angularity and dimensionality is to look at how materials bend or break. Objects that break into pieces and thus cannot bend are low dimensional. Take for example two materials, jelly and glass. Both these materials are transparent, but the jelly is soft, flexible, less tangible and lighter, thus high dimensional. The glass is hard, rigid, impenetrable and heavier, thus low dimensional. If you attempt to bend glass, it shatters into sharp pieces. If you attempt to bend jelly, it bends considerably until a chunk lets loose, but not with any sharp pieces. Angularity you will find plenty of in the most low dimensional materials: like crystals and carbon.

Because the macrocyclic level is higher dimensional (large scale size is a form of high dimensionality), angularity occurs more rarely in outer space, in that what we can observe through a telescope. Also, the state of equilibrium for the outer space medium is high dimensional, both on macrocyclic scale and mesocyclic scale. Angularity is most abundant in the microcyclic level, because the microcyclic level is lower dimensional. Spirals found in the microcyclic level are often angular. This again shows us the relation between angularity and dimensionality. Angularity occurs the most where there is low dimensionality.
 

Dr. John Rakovan (Miami University, Oxford, Ohio)

Image by John A. Jaszczak.

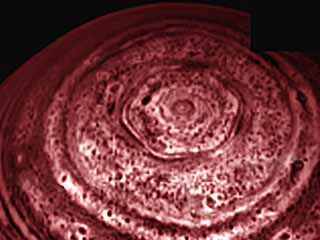Image by NASA/JPL, VIMS Team, University of Arizona

Left: Growth Spiral on Graphite. Millimeter Scale: A graphite crystal (3 mm across) showing spiral growth steps on the surface. Optical differential interference contrast photograph by Dr. John Rakovan (Miami University, Oxford, Ohio).

Middle: Growth spiral on 0.5 mm graphite crystal from Crestmore quarry, California. Image by John A. Jaszczak.

Right: This hexagonal spiral vortex was originally discovered during the Voyager flybys of Saturn in the 1980s. Nobody has ever seen anything like it anywhere else in the Solar System. The bizarre cloud pattern is shown above in a recent infrared image taken by the Saturn-orbiting Cassini spacecraft. The images show the stability of the hexagon even 20 years after Voyager. Movies of Saturn's North Pole show the cloud structure maintaining its hexagonal structure while rotating. Unlike individual clouds appearing like a hexagon on Earth, the Saturn cloud pattern appears to have six well defined sides of nearly equal length. Four Earths could fit inside the hexagon [text by NASA].

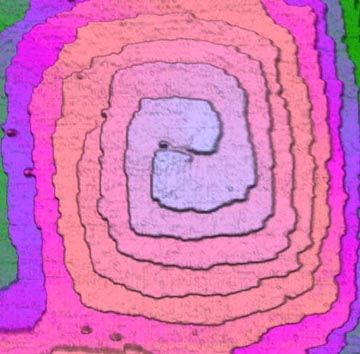
So what is the reason then that angularity occurs in vortices? For the answer, take a look at this photo below. It's a picture of a smoke ring. But it is not an ordinary smoke ring. As you can see, this smoke ring is not round but has an angular shape. It is hexagonal.

Hexagonal smoke ring. The growth of waves around a vortex ring is often called Widnall instability, after the researcher who first analyzed it. Here it has produced a remarkably symmetric pattern of smoke in air at a Reynolds number of about 1000. Photograph by G.J.Jameson & M.Urbicain [text and image from 'An Album of Fluid Motion' by Milton Van Dyke. Image was edited with text (numbers) and lines].

The six sides of the hexagon shape suggests that the number of movements in this vortex might be 6. This vortex belongs to the 8th dimension level. If we follow the Fibonacci sequence in the same progression that I mentioned earlier, with the spire starting at one, then the revolute should be the 9th Fibonacci number. The ninth Fibonacci number is 21, if we divide this number into a left and right turning number of meridians then the number is 13 and 8 (13 + 8 = 21).

So If any of the meridians for some reason should become visible on a revolute, I would have expected that number to be 8 if we can only see one direction of meridians, 13 if we could only see the other direction, or 21 if we could see all meridians. But the number of sides of this angular vortex suggests a number of 6. This leads us to a possible explanation for why angularity can occur. Namely that this vortex tried to form without the minimum number of meridians required for that vortex.
 

ANGULARITY IN VORTICES OCCURS WHEN A VORTEX TRIES TO FORM WITH A NUMBER OF MERIDIANS LESS THAN THE MINIMUM REQUIRED NUMBER OF MERIDIANS FOR THAT VORTEX
 

Angularity happens because the low number of meridians doesn't provide enough freedom of movement for the vortex to complete the movement in its complete form. Thus that is the explanation for this phenomenon. Keep in mind that the number of meridians are not limited to whole numbers, just like the dimensions are not limited to whole numbers. They are not limited to integers. A vortex can also lack half a meridian.

Another important detail is that the number of corners in an angular vortex is as always a non-Fibonacci number. The number of corners is never 1 or 2 or 5 or 8 or 13 or 21 or 34 etc. So you will never see a pentagonal (5 corners) spiral or an octagon (8 corners) spiral. The exception to this rule might be the number 3. There are some three sided crystals, like trigons on the surface of diamonds, and some snowflakes are triangular as well, but other than that the number 3 is rare in angular vortices. There are no spirals with three corners. Below are a few examples of angular vortices with four corners, all of them viewed through a microscope. 4 is not a Fibonacci number, nor are any of the examples on the rest of this page.
 

Image by Anthony R. Kampf, William. S. Wise and George R. Rossman

Image by Steven Higgins, Higgins Research Group, Wright State University

P.M. Thibado, B.R. Bennett, B.V. Shanabrook and L.J. Whitman for U.S.Navy

Fluid Polygons

Here's one more example of angularity. This time in fluids. Water is extruded from an annular gab. As you can see, the water makes a highly expansive outward movement (expansion is increase in dimensionality, contraction is decrease in dimensionality). Such a high dimensional movement requires a high dimensional medium, with a large number of meridians to continue. The water is not high dimensional enough to complete such a movement. The more the water radiates outward, the more tension builds up in its surface. When the maximum tension that the fluid can handle has been reached the shape becomes angular and splits into multiple vortices.

Photo by Robbie Buckingham and John W.M.Bush. Massachusetts Institute of
Technology. Taken from 'A Gallery of Fluid Motion', numbers were added

These multiple vortices that appear when the vortex splits are probably lower dimensional vortices, of a lower cycle. You can see that one of these examples does not split but succeeds in completing the movement by forming a bell (actually, it is a part of a suprabell). Once again I've put the number of corners in these vortices next to each image. None of these is a Fibonacci number.

Too Many Meridians

Angularity is a form of low dimensionality. The lower the number of meridians of a vortex, the lower the dimensionality of the vortex. A vortex can also contain a larger number than the required number of meridians. A high number and an abundance of meridians is a form of high dimensionality. The higher the number of meridians, the higher the dimensionality of the vortex.

This form of low or high dimensionality is irrespectively to the dimensionality level of a vortex. Even when the vortex type does not change by morphing, the dimensionality can change by the increase or decrease in number of meridians. It is possible to see in a spiral that it has more than the minimum required number of meridians if the spiral has more than two spiral arms. Some spirals have four arms that all connect at the center. Other spirals have spiral arms that split into more arms along the length of the arms. The shape of a vortex becomes more complex as the number of its meridians increase. While a low number of meridians leads to angularity, a high number of meridians leads to more curved movements within the shape of the vortex.

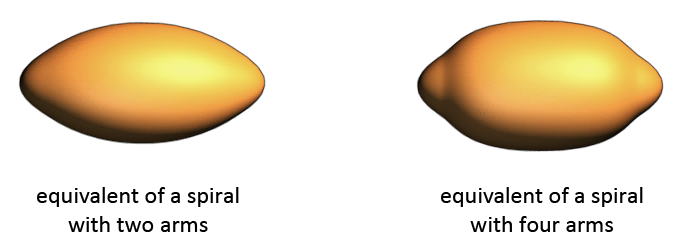
A bulb vortex doesn't have visible spiral arms, but it too can have a version that is the equivalent to a spiral with four spiral arms, just as there is a version of a bulb which is the equivalent of two arms. What happens is that the shape of these higher dimensional bulbs becomes slightly more complex as the number of meridians increase.

One method of increasing the number of meridians of a medium is by splitting. Forcing air through a series of rotating rotor blades will split up the air and increase the number of meridians in that medium. This will temporarily increase the dimensionality of air.

Tension and Compression

A phenomenon in which the number of meridians is that what causes the resulting effects is tension and compression in fluids. Here too it is the lack of meridians or the excess of meridians that plays an important role. The effects of tension and compression are described on a separate page. Better evidence for the theory of the existence of the meridians is also presented on that page.