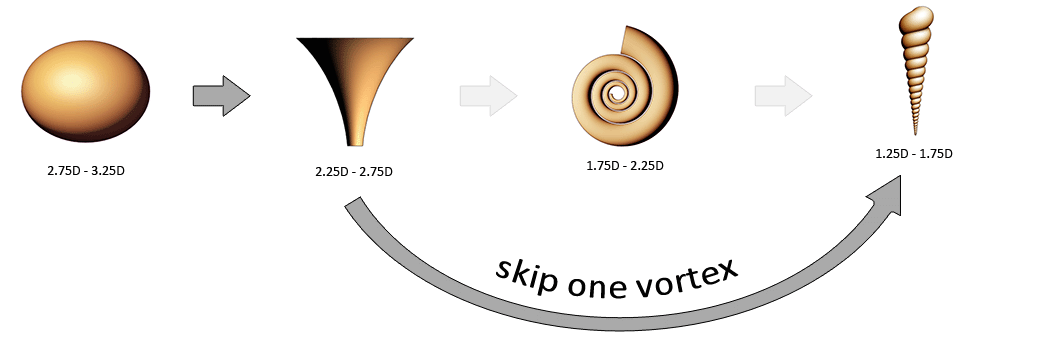
More about Vortices

Repeating Vortex Bridges

Most of the vortices that we encounter in our world are unconnected individual vortices. Only occasionally you will find two subsequent type of vortices, thus two subsequent vortices in the sequence, connected to each other. And less often than that you will find three or more different vortex types connected as one larger vortex. There is however one type of connection of a higher number of vortices that occurs quite often. That type of connection is the occurrence of repeating vortex bridges, and the spirals which they connect. Spirals of equal type and outer bridges of equal type can repeat themselves in succession by switching back and forth between spiral movement and bridge movement. Here below are a few examples of such repeating vortex bridges.

Repeating Swirl

Von Karman vortex sheet

Repeating Bulb

Effect of rotation on capillary instability. The instability of the jet of water, with excitation at wavelength 4.8 diameters, is increased by rotating it at 435 revolutions per minute. Rutland & Jameson 1970 [text and image from 'An Album of Fluid Motion' by Milton Van Dyke].

Repeating Revolute

Co-axial Vortex Rings. By T.T.Lim,
National University of Singapore.
 

Repeating Scrolls

Instability of smoke from a cigarette. These two views of a familiar phenomenon, photographed in a light draft, show that the initially rectilinear plume becomes unstable and forms two trailing vortices interconnected by a ladder-like network of vortex loops. Perry & Lim 1978 [text and image from 'An Album of Fluid Motion' by Milton Van Dyke].
 

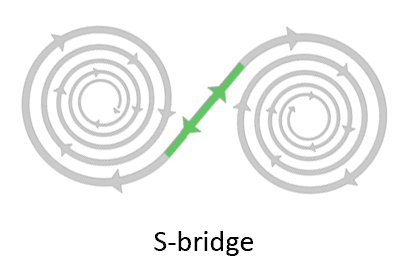
Of the four examples shown above, the first two connect with normal outer bridges. But the last two examples connect with a different kind of bridge. Outer bridges normally only connect two spirals that rotate in opposite directions, one is left-turning, the other is right-turning. But in the last two examples multiple spirals are connected that rotate in the same direction (difficult to see with the scrolls). The bridge that connects two spirals of equal direction is called an s-bridge. The bridge is named like that because the movement makes an s-curve from one outer end of a spiral to another outer end of a spiral.

The other example of a vortex bridge that can connect by making an s-shaped curve is the revolute. We have seen in previous examples how a revolute vortex connects to a cradle. We have seen examples of how the cradle, which is a bridge vortex between two opposing spirals, forms underneath the head of a mushroom cloud during some nuclear detonations. Now take a look at the video below, and watch carefully how the cradle forms underneath the head of this explosion.

At first, the upper part of the cradle forms itself the usual way, as we would expect. We are also used to see that not the entire cradle will form itself underneath the head of a mushroom cloud, because the opposing revolute spiral is not there. But this one seems to form itself to almost 50%, which is further then we have been used to from different examples at high intensity detonations. However, after it has formed itself to almost 50%, the cradle appears to contract instead of continue its normal path. The vortex was not able to complete its high dimensional move so it has run out of strength and it contracts back to the lower dimensions. The movement looks like an opposite movement of that of the revolute.

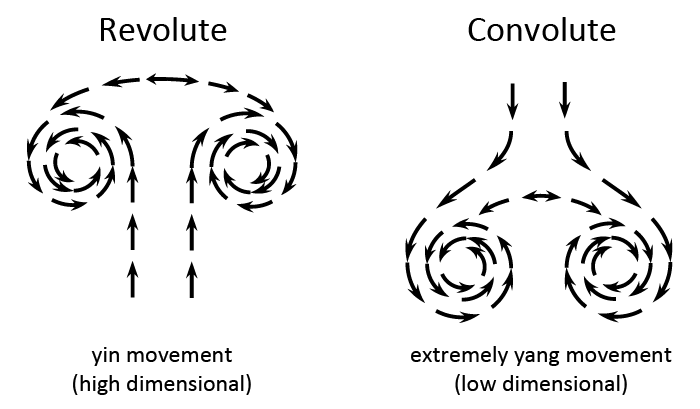
Such a movement is what I for now call a convolute vortex. What seems strange after closely evaluating this type of movement, is that the cradle now appears to make a contracting move instead of an expanding move. In fact, if you look at how the cradle now contracts inward, it looks like an exceptionally contracting move. But the cradle now proceeds as the unsual inward spiraling of the revolute windings, which is supposed to be an expanding move towards the higher dimensions, although that same move usually happens along the path of the first spiral arm, not the second spiral arm that connects to a cradle. The explanation that could make this illogical move logical is that both spirals at either ends of the s-bridge are of a different size. The half-cradle now proceeds to spiral inwards towards the smallest windings of the revolute, which is both an expanding move (flowing sequentially towards the higher dimensions), and a contracting move (scaling towards the lower dimensions). The scaling part of the move is likely to be much more contracting than the expansion that the flowing part of that same move accomplishes. The entire move is likely to be more contracting than expanding, because scaling takes much more energy than flowing.

This rotational vortex type is worth to mention despite the lack of information about this type of movement because so far I have seen different examples of a vortex with that same shape. Two other such examples are shown below. One is the blue whirl, a new type of flame discovered by the University of Maryland in 2016, the other is the Crab Nebula, a supernova remnant found in the constellation of Taurus. The upper part of the blue whirl looks identical to the outer shape of the convolute, yet no spiral windings are visible and the flow movement of the vortex is likely to be in the opposite direction to that of what is shown at the nuclear detonation, for those reasons that vortex is probably not a convolute, but it might be closely related to the convolute, and it might be a different type of s-bridge. The type of convolute that can be seen at the Crab Nebula is most likely to be of equal type to the one seen at the nuclear detonation, since both are formed by an explosion. The visual difference between the two is that the revolute vortex, or the head of the mushroom cloud, can not be seen in the photo of the Crab Nebula. That is because the state of equilibrium of the outer space medium is the revolute, therefore a revolute vortex can never be seen in outer space.

Image by University of Maryland

Image credit: Optical: NASA/HST/ ASU/J. Hester et al. X-Ray: NASA/CXC/ASU/J. Hester et al.

If you take a human hair, and hold a candle flame against the tip of the hair, then the hair will curl up chaotically, forming a shape that looks like the magnetic field lines of the sun. It could be that that movement is the same type of movement like the movement of the convolute. A bridge that makes an unconventional, contracting move. The convolute-like vortex that appears in the photo of the blue whirl connects to a vortex type that also forms the two coronal pole regions of the sun, the amplipole (perhaps also worth to mention: the circumferential regions of the corona look like strains of fiber).

Dedimensionalized Vortex Shapes

It is sometimes possible to find shapes within the environment that look like the shape of a familiar vortex, but one that is like a two dimensional version of the three-dimensional vortex, and that is elongated / stretched in the direction of the third axis. What you get is a vortex that looks simpler in shape than the original vortex, but is still recognizable as the vortex type of the original vortex.

One example of this can be a ravine whose inner volume is shaped like an amplicone that is stretched along the length of the ravine. You might think when observing such a ravine that the shape of the elongated ravine is unrelated to anything that has to do with an amplicone. A ravine itself is not formed by the movement of an amplicone. The similarity of the shape is just a coincidence. Furthermore, the elongated version of an amplicone does not appear to be a real existing vortex type. No such vortex has been observed.

However, the peculiar thing is that despite that the shape can be a coincidence, and that an elongated version of the vortex does not appear to exist, despite that the ravine can cause effects on its environment which are the result of the properties of an amplicone. The shape of the ravine can create vortex movement in the open space inside the ravine which is similar in effect of that of an amplicone.
 

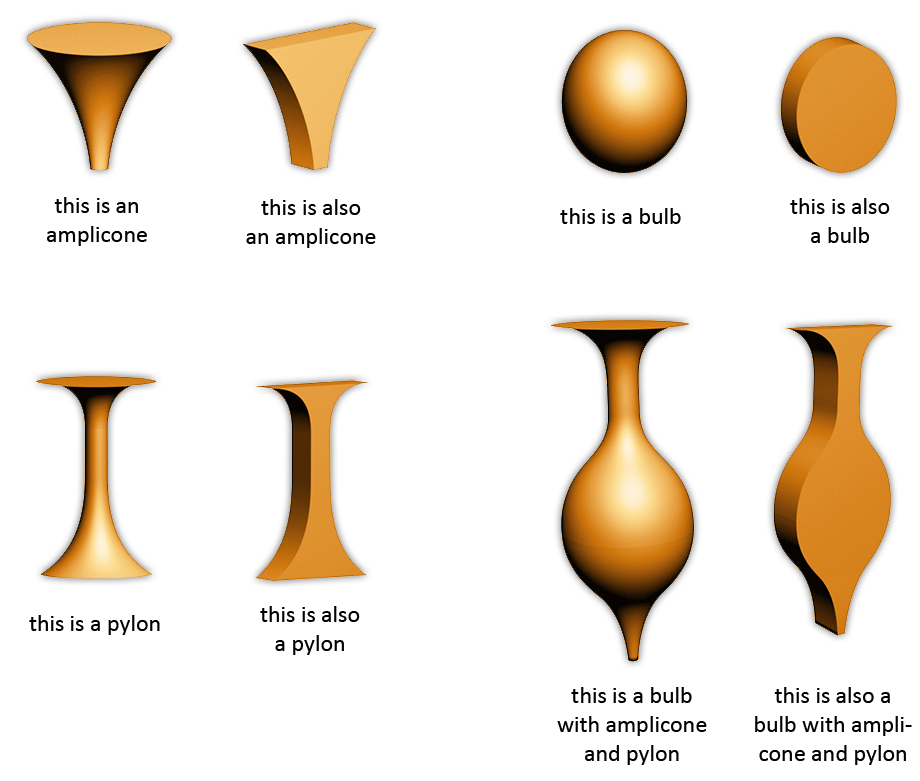
These elongated shapes that look somewhat the same as real vortices are what I call 'dedimensionalized vortex shapes' (bear in mind that the spelling is 'dedimensionalized', not 'dedimensionized'). These dedimensionalized vortex shapes are not vortices. I do not know what vortex forms inside or outside of these shapes because I haven't seen an example so far that shows a visible vortex. It could be that these shapes produce multiple vortices along the length of the extruded shape. It could also be that a type of vortex forms that we are still unfamiliar with. A dedimensionalized scroll looks very much the same as a disc spiral, so it could be that for some other spirals other dedimensionalized vortex types exist that look similar.

There is also a word that describes the opposite direction of this phenomenon. That word is 'extra-dimensionalized'. In the images above, the shapes on the right sides are dedimensionalized versions of the shapes on the left, and the shapes of the left are the extra-dimensionalized versions of the shapes on the right.

Different examples show us the length of extrusion for a such a shape can be very short to very long. What difference this length in the direction of the third axis makes is not clear to me. I'm also not sure if a short and a long extrusion produce the same kind of vortex movement, or movement from different vortex types, or a different number of vortices.
 

Spirals can also have a dedimensionalized vortex version. And dedimensionalized vortex shapes also exist of binary spirals, and thus also of bridges that connect spirals.
 

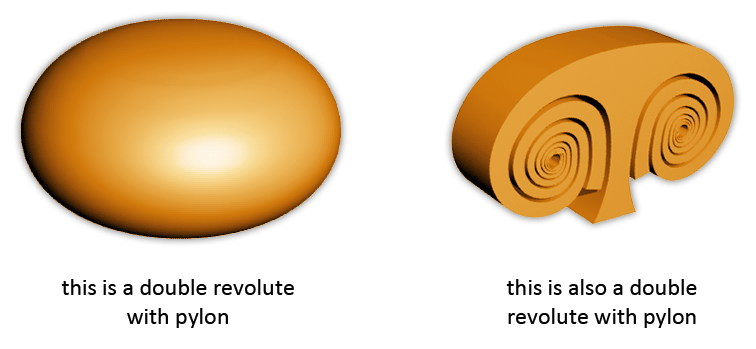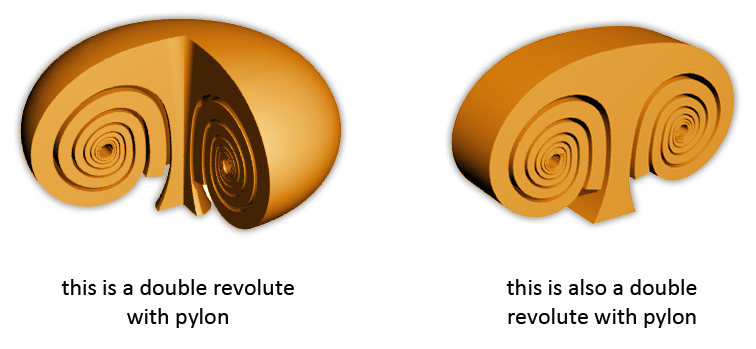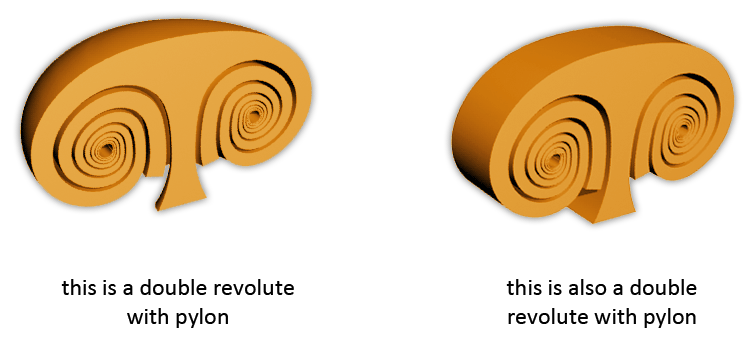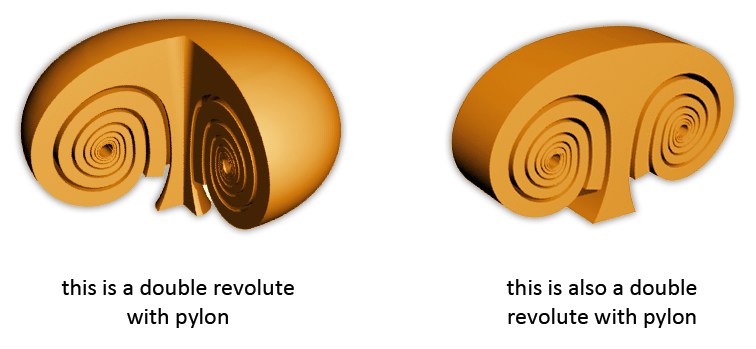
Some examples of these shapes, and their effects, will be shown on the page about sound, and the page about tension and compression. On this page I will show two examples, one are airfoils, the other is a vortex on a wedge.

Example #1 – Airfoils

Image by Meggar (Wikimedia), under CC BY-SA 3.0 license
 

The cross-section of an airplane wing is called an airfoil. The airfoil is a good example because a wing is a long extruded shape. The shape of an airfoil is somewhere between the shape of an ascended bulb, double bulb or bulb with amplicone. An airfoil is a dedimensionalized version of those vortices.

This proofs that a dedimensionalized vortex shape has effects on its environment that is in some ways similar to the effects of the shape of a bulb. This is because the bulb is the state of equilibrium for air. The most efficient shape to move through air is the bulb. And because not just a bulb, but also the shape of a dedimensionalized bulb is aerodynamic, it tells us that some of the effects of this shape are the same.

Example #2 – Vortex from a Wedge

When a shock wave passes through water in which a wedge is placed, then the tip of the wedge will produce a highmorph disc spiral. The reason for this is that the wedge is shaped like a dedimensionalized helicone, which makes it behave like a helicone vortex and thus is able to connect to a disc spiral, which is the prior vortex in the sequence. The ladder vortex induces the spiral vortex. A wedge is like a triangle that is extruded along the third axis. A helicone is like a triangle that is rotated around its length axis. Both shapes look similar when viewed from the direction as in the images below.

Left Image: This schlieren photograph shows the vortex that spirals from the tip of a thin wedge after the air is set in motion normal to it by the passage of a weak plane shock wave, which is out of sight at the bottom. Other photographs show that the flow pattern is 'conical' or 'pseudo-stationary', remaining always similar to itself but growing in size in proportion to the time. Photograph by Walker Bleakney [text and image from 'An Album of Fluid Motion' by Milton Van Dyke].

Another example is shown in the video below, yet here the shape of the vortex is not dedimensiozalized, and it is the disc that forms the helibar, not the other way around like in the previous example. This example shows what happens when water flows past a disc shaped object at high speeds. Because the object is shaped like a disc the water that flows past the edge of the object forms a helicone. You can clearly see the helical rotation of the vortex in the slow motion video.

This helicone is actually more shaped like a helibar. It looks more like a waterspout and less like a land tornado. The helibar is like a weaker version of the helicone (less strong contraction), both are close to each other in terms of dimensionality. The same holds true for barred spiral galaxies. When the spiral arms are weaker (thus a weaker contracting or expansive force) they tend to form the shape of helibars instead of helicones. Most bars in spiral galaxies are of the weaker form.

The disc is too thick to be shaped like an unmorphed disc vortex. If the disc would be thinner, then the vortex it would form might look more like a helicone. I haven't found any such example in water, but I have found one such example in air, which are wingtip vortices generated by either the tip of the wing or by wingtip vortex generators like in the image below.

Image by Ahunt (Wikimedia). Image was cropped.

The reason this works is because the vortex generators are thin plates with a round side to it. The round side of the vortex generators act like part of a disc, which then produces a helicone. If the airplane travels at high speeds, the wingtip vortices are formed by spires. At lower speeds it is formed by helicones.

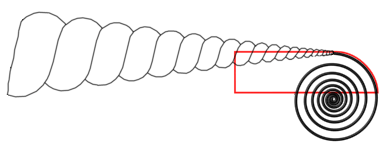
Vortex Embedment

Spirals can show a particular behavior in which the presence of one type of spiral, with the inclusion of a force of movement, can induce the creation of another smaller spiral, that is 6 dimension levels lower than the first spiral. This process also requires the presence of a fluid that is a different kind of fluid of which the first spiral is made of, and which will be the fluid in which the second spiral will form. Two examples of this type of phenomenon were already shown on the page about the outer bridges.
 

This pairing of two different vortex types so far only appears to happen with spirals, and in some cases the larger of the two spirals is not visible to the naked eye, although through experiment and by carefully examining the situation one can be certain that the vortices are there.

This phenomenon is what I decided to name vortex embedment. Whenever this phenomenon occurs, one vortex is embedded into another vortex that is six dimension levels higher than the vortex that is embedded. The smaller vortex is called the 'embedded vortex'. The larger vortex is called the 'vortex embedder'. Examples of this phenomenon are listed below.

Example #1 – Swirl Embedded into a Scroll

In the image below you see two oppositely mirrored spiral vortices being created in the clouds behind an aircraft. Behind the airplane is an invisible vortex sheet, consisting of two scrolls that emerge from the tip of the wings, connected by a wake belt, which is an outer bridge between the two spirals. The two spirals that you see in the photo are two swirls, which are two spirals that are exactly 6 dimension levels lower than the two scrolls. The two swirls are created in the cross-section of the two scrolls, the inward rotating movement of the swirls is induced by the inward rotations of the scrolls. An example of this was already shown on the page about the outer bridges. In this example it is a vortex of the tenth dimension level inducing the creation of a smaller vortex of the fourth dimension level.

Image by Bernal Saborio, under CC BY-SA 2.0 license

Example #2 – Disc Embedded into a Revolute

What you see in the photo below is a vortex that appears to consist only of a thin line, but there is another vortex in the image which is not visible to the naked eye. When a piston is pushed through a circular nozzle underwater, a vortex ring is created. In this case a revolute vortex is created at the exit of the nozzle. What you see in the image is only a cross-section of that revolute vortex, which appears when a dye is added to the water. But the cross-section is not merely a segment of the revolute vortex. The line in the image is a new vortex type, created by the dye, which is exactly 6 dimension levels lower. The revolute vortex induces the creation of two disc spirals, connected by an enexus bridge. An example of this was already shown on the page about the outer bridges. In this example it is a vortex of the eighth dimension level inducing the creation of a smaller vortex of the second dimension level.

Formation of a vortex ring from a nozzle. Water is ejected from a sharp-edged circular nozzle of 5-cm diameter into a tank of water by a piston that moves at a constant speed of 4.6 cm/s after accelerating for 0.3 s. The rolling up of the vortex sheet that separates from the edge is shown by dye injected there. The piston stops at 1.6 s, and the vortex ring then induces a secondary vortex of opposite circulation. Didden 1979 [text and image from 'An Album of Fluid Motion' by Milton van Dyke].

Example #3 – Light Embedded into a Bulb

Why do elliptical galaxies emit so much light? At first one would not expect that to happen because elliptical galaxies are bulbs, and bulbs are located at the central balance point. Light is located at the zero point, which is located at a much lower position in the transformation sequence. The reason is that light is embedded into the bulb. The presence of the bulb, along with other factors, induces the creation of a lower dimensional light vortex, which is exactly 6 dimension levels lower than the bulb. In this example it is a vortex of the sixth dimension level inducing the creation of a smaller vortex of dimension level zero.

Image by European Southern Observatory (ESO),
under CC BY 4.0 license

This could mean that there are more elliptical galaxies in the universe than we might realize, because it is assumable that not all ellipticals will have a vortex embedded into them. There might be more ellipticals out there, subsisting in darkness, and thus less detectable within the visible light spectrum.

Connections with One or More Steps Missing

When two vortices of a different type connect to one another, then the usual tendency is for these two vortices to be two subsequent vortices in the sequence. The high end of one of the two vortex types has the same dimensionality value as the low end of the other vortex type, it is for that reason that those two vortices can connect. But sometimes, in some more rare situations, two vortices can connect which are not subsequent vortices in the sequence. In that case one or more steps in the sequence is skipped so that one or more vortices that are supposed to be in between the two other vortices are missing, but the other two vortices still form one seamless connection. Such a connection creates a high amount of pressure, or it creates a high amount of tension, and both those scenarios occur when there is high velocity and strong forces involved.

On this page I will show you two examples. Both examples are spiral-ladder sequences. Both examples show one vortex missing. And in both examples the vortex that is missing is located at the same distance from the central balance point (the swirl is located 1.0D below the central balance point, the revolute is located 1.0D above the central balance point). Both examples involve a high speed jet that is aimed towards a nearby flat surface. And both these examples also show the presence of a bridge connection to a bulb, which is the endobar when the swirl is missing and the exobar when the revolute is missing. Both these bridges are located at the same distance of 0.25D from the central balance point in the transformation sequence. One of the bridges is located above the central balance point, the other is located below the central balance point.

Example #1 - Jet from a Bubble Near a Wall

The first example is one where a laser light creates a bubble in still water, and then this bubble collapses near a wall. During this collapse, a spike forms at the bottom of the bubble that extents towards the wall further below the bubble. In this case it is a bulb connecting to an amplicone, which connects to a helicone. But the usual scenario would be for an amplicone to connect to a swirl, which then connects to a helicone. It is the swirl that is missing in this picture.

This sequence shows the effect of a high speed jet, directed downward, that forms at the top of a bubble during collapse. In this magnified view the jet is visible only as a thin dark vertical line through the bright spot in the middle of the bubble. Passing through the almost empty cavity, the jet impinges on its bottom and carries it along to form the spike that extents toward the wall. The jet is believed to extend far ahead of the spike, and to be the cause of cavitation erosion from a solid wall. The horizontal diameter of the bubble is about 2 mm. Lauterborn 1980 [text and image taken from 'An Album of Fluid Motion' by Milton van Dyke. Image was edited with text and lines].

If you look closely at the bulb in the photo above (the bulb is the bubble) then you can also see an endobar through the bright spot in the middle of the bulb. The presence of the endobar indicates that the bulb is a double bulb, which is the equivalent of a spiral with two spiral arms, otherwise the endobar would not be able to be there because it needs to connect to two spiral arms (or in this case, the equivalent of two spiral arms in the form of a double bulb). In this example it is pressure that is created in the helicone, because of the absence of the swirl. The swirl should have decreased the number of meridians within the flow of its path before connecting to the helicone, but because the swirl is missing, there is an abundance of meridians within the helicone which creates a high amount of pressure.

Example #2 - Laminar Jet Colliding with a Surface

In this second example a liquid jet collides with a flat solid surface which radiates the movement of the flow in an outward direction. The movement creates a series of rings onto the flat surface, with annular layers in between the rings. It is likely that the annular layers are either aureole belts or laminar belts, that connect as repeating vortex bridges (see the text and images about the repeating vortex bridges at the start of this page). In this case it is a bulb connecting to a pylon, which connects to a belt. But the usual scenario would be for a pylon to connect to a revolute, which then connects to a belt. It is the revolute that is missing in this picture.

Image by Mario Errico

To investigate the importance of the jet shape on splashing, perturbations of known frequency or amplitude are imposed on the surface of a smooth laminar jet. The varicose deformations imposed on the jet surface alter the flow quite dramatically [text and image taken from 'An Album of Fluid Motion' by Milton van Dyke. Image was edited with text and lines].

If you look in the photo at two bulbs that form above the pylon then you see that they are connected with an exobar. The presence of this exobar might be a requirement for two vortices to be able to connect while one vortex in between is missing. This might be so because the first example also showed the presence of bridge, which in that case was the endobar. In this example it is tension that is created in the aureole belts / laminar belts, because of the absence of the revolute. The revolute should have increased the number of meridians within the flow of its path before connecting to the first belt, but because the revolute is missing, there is a shortage of meridians within the belts which creates a high amount of tension.