State of Equilibrium

Helmholtz Resonator

The next clue came from a human invention. The Helmholtz resonator. Invented in the 1850s by Hermann von Helmholtz. It is a device that is able to oscillate air. If you look at its shape, you'll find that it resembles the shape of a bulb, with an amplicone at one end and part of a pylon at its other end.

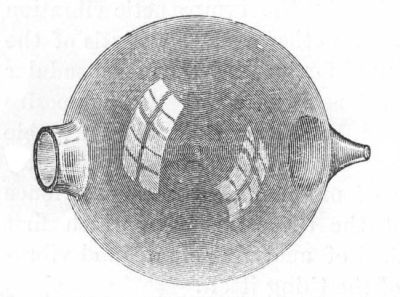Image from 'On the Sensations of Tone' by Hermann von Helmholtz and Alexander John Ellis

Because of this device, it becomes evident that air oscillates around the center of the bulb (And with center I mean the center location of the vortex within the transformation sequence, not the geometrical center of the shape of the vortex). From here on there are two possibilities: every material oscillates around the center of the bulb, or every material oscillates around the center of one particular vortex.

The first possibility is not without logic, because the bulb is also the exact center of the first half-cycle of the sequence. But if this was so than every vortex except for the bulb itself would deform very strongly as it starts to oscillate around a position that has a large offset to its own center position.

The correct answer is close to what was described as the second possibility. Every inorganic material oscillates around the center of one particular vortex, but these are only the materials that have only one state of equilibrium. Materials that have two or more states of equilibrium most probably oscillate around different centers simultaneously, thereby exhibiting a more complex movement that is a combination of several movements added together.

The next useful link I found in metal. Metals have characteristics that clearly differentiate them other materials. In general, metals are not hard to identify. Metal is lower dimensional (more yang) than air or water (harder, heavier, less freedom of movement), so the vortex that should be absent in metal should be lower dimensional than the swirl. So the vortex that describes the movement of metal should be one that lies below the swirl in the transformation sequence.

When we look at the question as to how metal oscillates, think about holding a metal bar in your hand, and with great force you strike that metal bar against another metal bar. You can imagine that would hurt a lot. But what exactly is that energetic movement that you feel? What vortex would best describe this intense vibration of the bar? I would expect that most of you will say that the disc is one of the more probably answers to this question. It is the vortex that drives this type of oscillation. And there are ways to give more confirmation to this hypothesis. Ways to make this more certain. Next we look at another human invention.

Clock Spring

A clock spring is a type of spring used in clocks / timepieces. It controls the rate of oscillation of the balance wheel. Together these two parts form a harmonic oscillator, keeping the speed of movement, and thus the time accurate. The piece you see in the image below is, like all clock springs, made of metal. And it is quite clear that its shape resembles a disc spiral (with the difference that the spiral arm is not a line but a strip). This alone does not proof that metal oscillates around a disc, because there are more types of springs that can be made from metal.
 

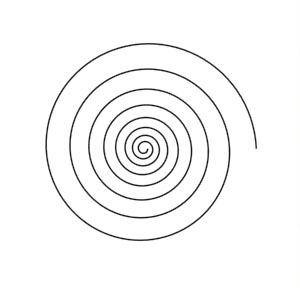Image courtesy of David West, Dave West Clocks

The difference between this clock spring, and all other spring variations, is that the clock spring is the one that gives the longest oscillation, significantly longer than a spring shaped like a helix. Also, when you construct this same spring out of a different material, lets say plastic, then it will not oscillate as well as it would if made of metal. From this we can say that the disc is in some way linked to the material metal.

So now we know that oscillation is a direction to look at when trying to find new pieces of the puzzle. From here on we know that it is likely that other materials will show a similar logic when that material is brought to oscillate. Now we've found 4 different equilibria within the first half-cycle of the sequence. Needless to say we want to find more. For a moment we leave oscillation for what it is, and focus our attention in yet another new direction.

What is the most efficient way to move through earth?

Image from 'Archie - De Terreur van de Ijsgeesten' by Edward Kearon (Ted Kearon)

The above illustration is taken from a 1982 comic book released by Oberon B.V. This fictional vehicle was designed to dig through the earth. It is a way how a comic book artist would illustrate such a vehicle in a form that would make it more or less believable that it would be able to perform such a task. It is a fictional vehicle, it would not be able to fully function the way it does in the comic if this vehicle would be build for real, yet its shape is not without logic.

The shape of the two screws looks most like the shape of a helicone. A helicone is a logical choice when trying to come up with an effective design for a tool that can successfully dig through earth. The shape and direction of movement of a helicone is what is close to being the best type of movement to penetrate through earth as a material. This shape and movement will not be of much use when trying to penetrate metal, rock or glass.

Left image from 'Archie - De Terreur van de Ijsgeesten' by Edward Kearon (Ted Kearon)

This vehicle was an example taken from fiction, but we do find the same clue in the designs of real machinery, as you can see in the image below. The movement of the ground drill on the left is closest to that of the movement of a helibar. The one on the right is closest to that of the movement of a helicone. Different types of soil, ranging from lower (more yang) to higher (more yin) dimensional, require different types of movement and shape of the blades to dig through the earth with the least amount of resistance. The material that matches the shape of the helicone the best is likely to be marl, which is a very soft rock. Marl is like a hard form of earth.

So now we found that one material has at least one type of vortex movement that is most effective as being the best movement to penetrate through that material. From here on we can expect that other materials too will have such a relation with one or more movements of particular vortices. So the logic thing to do is to look at other materials.

What is the most efficient way to move through air?

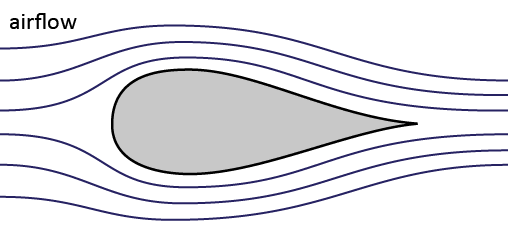
I used to be a student in Industrial Design, and I remember a lecture where we were told that there was an era within the early twentieth century in which it was believed that the teardrop shape is the most aerodynamic shape possible. For that reason some cars in that era were designed in the shape of a teardrop. Nowadays we know that this statement is not completely correct, at least, the statement is oversimplified and more factors should be taken into consideration when trying to come up with an efficient aerodynamic shape for a particular vehicle. For instance, the best possible aerodynamic shape depends on the speed of a moving object.
 

Image by Tom Demerly, Bikesport Inc.

Image by Cambridge University Eco Racing (CUER)

Image by Karelj (Wikimedia), under CC BY 2.0 license. Image was cropped and background faded

Image by Graham Bould. Image was cropped and edited with surface blur

The teardrop shape looks like the shape of a bulb with an amplicone at one end. This is because the shape of least resistance for an object to travel through air is the bulb. But this rule only applies to when an object travels at moderate speeds, at very high speeds the shape that is most effective in traveling through this medium becomes one that resembles a lower dimensional vortex, like a spire or rotating hyperbelt, and eventually, at ultrasonic speeds the hyperkone (most likely with a rotation).
 

bulb	lowmorph bulb
Image by Petey21 (Wikimedia), under CC0 1.0. Image was edited by removal of background	Image courtesy of the Gerald R. Ford Presidential Museum. Image was rotated 8 degrees CW and background removed

Another example is the comparison of the European soccer ball with an American football or a rugby ball. The first has the shape of an unmorphed single bulb, the second has the shape of a lowmorph double bulb. One is the equivalent of a spiral with only one arm and the other is the equivalent of a spiral with two arms. The American football is a morphology between a swirl and a bulb, while the soccer ball is centered around one vortex type only. I expect that either only one of the two is the most correct vortex that belongs to air, or that the most correct vortex and thus shape/movement depends on the weather conditions of the environment, and thus can shift from one vortex to another over time.

I need to make a small note here that a teardrop shape is not the shape of how droplets of water fall. I use the word teardrop because when I do so everyone knows what shape I refer to. We know what shape to imagine that goes along with that word. But in reality a falling droplet of water takes on a different shape.

What is the most efficient way to move through metal?

The above image shows a circular saw blade used for cutting metal. The shape and movement of the blade comes close to the shape and movement of the disc spiral, with the absence of the inward circular motion, but with the inclusion of the circular motion. This tool demonstrates for us that the disc spiral comes close to being the best possible shape and motion for movement through solid metal.

The disc is a vortex from the first half-cycle. There are more disk-shaped vortices within the third half-cycle, with either a single or a double rotational movement (the meridians move in two opposite directions simultaneously). It is likely that all those disk shaped vortices are state of equilibriums of different types of metals. If this one spiral from the first half-cycle is also a state of equilibrium of one or more type of metals is therefore not entirely sure. I suspect that is because spirals are able to oscillate. And metal can oscillate. It has so far not been determined that the disk vortices of the third half-cycle are vortices that are able to oscillate. For this the vortex needs to have to ends with a different dimensionality value.

What is the most efficient way to move through water?

We already know that we've never seen a swirl spiral underwater, so we are expecting that the swirl is the state of equilibrium of water. To be more sure about this we can look at how the shape and movement of this vortex behaves in water. We can attempt to find out if that shape is the shape which gives the least resistance when moving in water.

If the swirl is the shape of least resistance, then perhaps fish could be shaped like swirls. The body of a bird is shaped more or less like a bulb with amplicone. But there are no fish that are shaped like a swirl. It is not to be expected that there are fish that are shaped like a swirl, because the shape of the swirl is too complicated. There are however many fish shaped like a bulb. Here, we do not find evidence for the swirl being the shape of least resistance in water.

Image by Roland zh (Wikimedia), under CC BY-SA 3.0 license

When nature does not provide us with all the answers, we turn our heads towards human inventions, and there we find the water propeller. The shape of a water propeller, and its axis of rotation, is closely related to the shape of a swirl. It induces the vortex movement of a swirl, and thereby it is the fastest way to propagate through liquid water.
 

Image by Ing. Dino Piacci (Wikimedia). Image background color was altered, centerpiece softened

Another way to find this relation between water and the swirl is to ask yourself: what is the fastest way for a human to swim? How do your arms move?
 

Water Turbines

A Francis turbine is a type of water turbine that has an inward flow. This invention is more efficient than a typical water wheel. It is more efficient than a water wheel because both inventions mimic the shape of movement that water wants to make, but a Francis turbine mimics the correct type of movement better than the water wheel does. Francis turbine = swirl. The turbine is shaped like a swirl, which is the state of equilibrium for water. The more the shape is different than the shape of the swirl, the more energy it will cost to make the water flow in that 'less desirable' shape, thus the more energy will be lost. This is partly because of an increased buildup of forces of tension and forces of compression within the flow of the water.

What is the most efficient way to move through outer space?

We already know which vortex is absent in outer space. And we've already seen one example of a medium for which we knew which vortex was always absent in that medium and later we also found the logic that showed that that vortex was the shape that could move most efficiently through that medium. Let us assume for a while that this link we think we've found is correct. Let us assume that the state of equilibrium for the outer space medium is the revolute. Than this would imply that the revolute is also the shape of least resistance for travel through that medium.

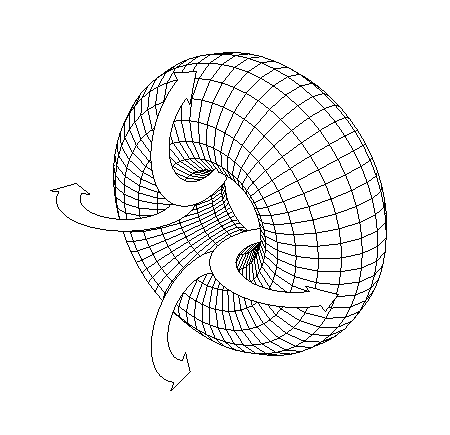
THE SHAPE OF LEAST RESISTANCE IN OUTER SPACE, ON A MACROCYCLIC SCALE, IS A THICK REVOLVING TORUS

So the shape of least resistance for the outer space medium is that of a torus with a small ring radius and large diameter for its cross-section. But this only applies to the macrocyclic level. The revolute is the state of equilibrium of the outer space medium at a macrocyclic scale. It is likely that on a mesocyclic scale the outer space medium has a different state of equilibrium. Because the outer space is a vacuum, it is likely that that state of equilibrium on a mesocyclic scale is either a vortex classified as a suprabell. So it should be a vortex from the fifth half-cycle.

When we want to build a spaceship, or anything that travels through outer space, then the shape of the revolute will not be of any use, or you would need to build a ship that is immensively huge. And from what we have learned from the example of the bulb in air is that for very fast speeds we would need a lower dimensional vortex. The shape and movement of the revolute is also difficult to fabricate. Still we might wonder how one day we might benefit from this acquired knowledge.

What is the most efficient way to move through crystal?

What holds true for all the materials that we know as crystals also appears to hold true for water in crystallized form: ice. We all know how an icepick looks like. We know why an icepick is shaped the way it is. You can imagine that such a shape, thrust forward in a straight line, would be close to the best shape that can penetrate crystals. A rotational movement doesn't work as well with crystals as it does in other materials. Nor does any bending around corners or curved movements. The icepick, its movement and shape, is related to the spire.

Here is another example of a spire penetrating crystal. Its a Shaolin monk throwing a sewing needle through a glass shield, captured at 1000 frames per second.
 

If you observe ice in different conditions and environments then sometimes you can also find ice in the form of spikes. This is another sign that the spire is the vortex that belongs to ice. The spire is also the state of equilibrium for other crystals, but the exact position within the transformation sequence can differ per type of crystal. Sometimes the state of equilibrium for a crystal lies close to the monolith or the hyperkone. Diamond is a type of crystal material which state of equilibrium is a hyperkone. Such a material - vortex relation is something we would expect, because diamond is the hardest material known to man, and the hyperkone is the lowest dimensional vortex in the first half-cycle. Lower dimensional means harder, more difficult to penetrate. Higher dimensional means softer, easier to penetrate.

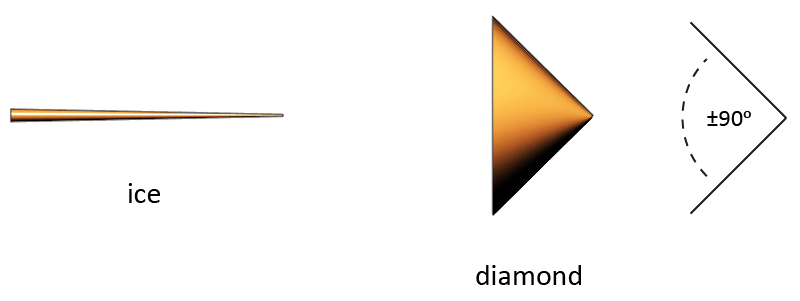
The drawing above is probably not the most correct representation for the vortex that forms the state of equilibrium of diamond. A diamond, like most crystals, does not want to be round, a diamond has an angular nature. Angularity is a form of low dimensionality. If the above drawing would be correct than diamond would be less hard than it is now. If two vortices are identical, but one of them is angular, then the one being angular is lower dimensional than the one that is not angular, despite that their basic type is the same. This is because of the extra lack of movement of the spire. A vortex that is angular has a lower meridian count (less paths of movement) than a non-angular vortex, thus less flexibility, more rigidity.

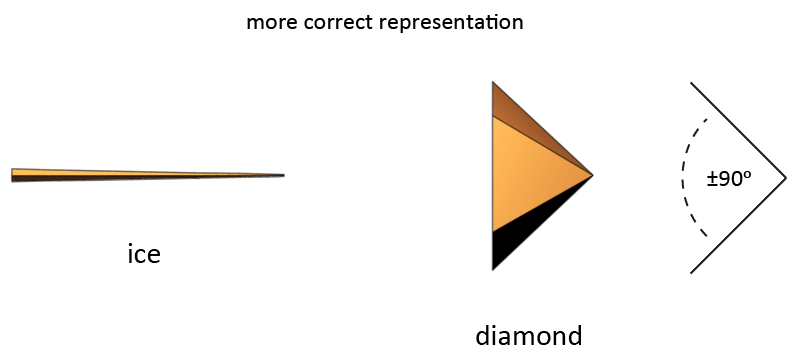
Diamond breaks light in a different way than the vast majority of other crystals. It has a relatively strong ability to disperse light of different colors (high optical dispersion), and has an extremely high refractive index. This could be caused by the rotational movement of the cone, which is in fact a spiral, not a ladder like the spire.

The number of sides for a diamond could be somewhere around 6, but this is not sure. Some raw diamonds show 4 sides, or three. Many cut diamonds look almost round, or have much more sides than six, but this is also because of the way the diamonds are cut, not always how nature intended it. But the hyperkone for a diamond should be angular.
 

Image by United States Geological Survey

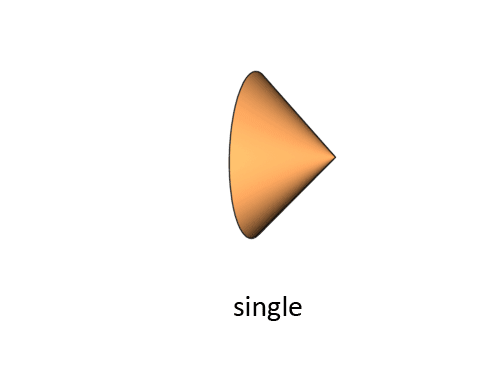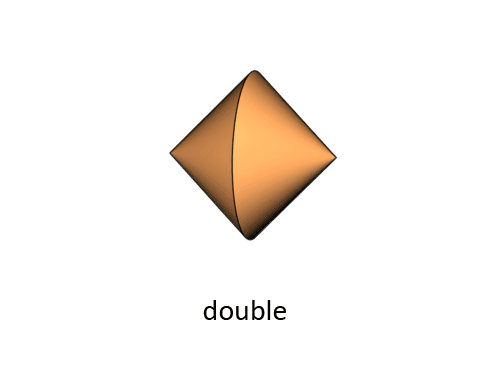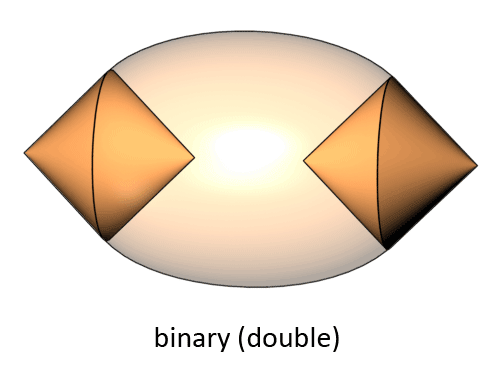So these are the states of equilibrium that we found so far show: crystal, metal, earth, water, air and the outer space medium.

So lets use the same logic we used for the previous states of equilibrium and now use it for other materials. Lets start with oscillation. How does earth oscillate? Well, there is one direction to look for: earthquakes. Earthquakes take place within the earth's crust, thus in rock. It could be that earthquakes are driven by oscillation of a vortex. It depends on what earth layer, and which type of earth material is the source of the earthquake, to know which vortex is the cause of the oscillation. It could be that the helicone is the vortex that is responsible for earthquakes. But there are not enough clues at this moment to confirm that.

How about rock? How does rock oscillate? Crystals can oscillate but rocks can not. Not all materials can oscillate so we can not find the state of equilibrium for every material by looking at its ability to oscillate. For rock we need to look at one of the other methods.

What is the most efficient way to move through rock?

This one is not so difficult to solve. Below you can see a picture of a pneumatic rock drill. The shape of the end of the tool is that of a monolith, an inner bridge vortex. The movement that the rock drill makes is also the same as that of the monolith: in one direction without a rotational movement. The position of the monolith within the transformation sequence is also a logical one. It is located close to the spire, both vortices are among the lowest dimensional in the sequence, and both rock and crystal are low dimensional in the sense that they can not bend.

So what I found is that for every medium a vortex exists whose shape and movement gives the least resistance for movement through that medium. This shape and movement is also that which provides the most stability for moving through that medium. With other vortex movements, the motion becomes less stable. The properties of those mediums are linked to the properties of those vortices. Many properties of each materials can be explained by understanding which vortex the material is linked to. This link we call the state of equilibrium. It is a fundamental relationship between vortex movement and matter that we find in the world around us.

The monolith is an inner bridge, so for the first time we've found a state of equilibrium that is formed by the properties of a bridge vortex. The reason that rock can not oscillate is the same reason that the monolith can not oscillate. A bridge vortex has two ends of equal dimensionality. For oscillation to take place, we need contraction and expansion, the material needs the ability to go back and forth between low dimensionality (yang) and high dimensionality (yin). Thus for materials whose state of equilibrium is a bridge or a tunnel, this is not possible (it might be possible when a tunnel is half a tunnel).

OSCILLATION CAN ONLY TAKE PLACE IN VORTICES IN WHICH BOTH ENDS HAVE AN UNEQUAL DIMENSIONALITY LEVEL VALUE. THUS OSCILLATION CAN OCCUR IN SPIRALS AND LADDERS, BUT CAN NOT OCCUR IN BRIDGES OR TUNNELS.

How Does Water Move Through a Hole?

There have already been two methods by which we could conclude that the swirl is likely to be the state of equilibrium for water. If we look at how water moves through a hole, then again the observations lead to the same vortex. Although here there is more than one possibility. Water that expels through a hole forms a swirl with a whirlpit underneath. So it can be the swirl that is the state of equilibrium, or the whirlpit, or both combined. Because of the previous clues that we found it is likely that the correct answer is solely the swirl.
 

Image by David Baird (Wikimedia), under CC BY-SA 2.0 license

If a whirlpool forms when water expels through a hole then the liquid comes out as an air-core vortex

Water that pours out of a bottle can do so in the form of a non-hollow beam of water, which we see most often, but it can also easily do so in the form of a hollow whirlpit. If a whirlpool forms within the bottle of water then the water that comes out of the opening is a whirlpit, an air-core vortex. You can test this by shaking the bottle in circles a couple of times as the water starts to run out of the opening, that will create the whirlpool. The whirlpit is a vortex that is located close to the swirl in the transformation sequence, for that reason the whirlpit is one of the first vortices that becomes visible in water that has motion.

How Does a Superfluid Move Through a Hole?

Superfluidity is a state of matter, different from solid, liquid or gas, in which the matter behaves like a fluid without any viscosity. The liquid appears to be able move by itself in a way that defies the forces of gravity. The substance will rise up the sides of a container in which an amount of the substance is placed, but will do so without restriction, and will move right up the sides of the container and over the top. So you can't store a superfluid liquid in an open container, it would escape.
 

Video taken from a documentary by the BBC

Image by Alfred Leitner. Image was edited with arrows

One of the most spectacular results of these properties is known as the thermomechanical or "fountain effect". If a capillary tube is placed into a bath of superfluid helium and then heated, even by shining a light on it, the superfluid helium will flow up through the tube and out the top.

If you look at these images and observe how the superfluid moves, then it is not that hard to determine that its movement closely resembles the movement of one of the suprabells. It is the movement of the fifth half-cycle that drives the superfluid. Apparently, the state of equilibrium of the helium has moved towards the fifth half-cycle. But this can not have happened through dilative morphing. Lowering the temperature of the liquid helium should make it lower dimensional on the mesocyclic scale (and higher dimensional on a microcyclic scale), and dilative morphing is a yin process, it makes the liquid higher dimensional on the mesocyclic level (and lower dimensional on the microcyclic). The liquid progressively becomes lower dimensional with the lowering of the temperature, and the moment that the liquid helium turns into a superfluid some kind of reaction must take place that suddenly turns the liquid to very high dimensional. Yet what this reaction is uncertain at this moment.

At least one of the suprabells is the state of equilibrium for superfluids. Because the liquid superfluid-helium is a visible substance, whose movement can be observed, we can study the superlfuid-helium to learn more about the movement of the suprabells. The suprabells are also the states of equilibrium for vacuums. But since all vacuums are invisible we are more limited in studying those mediums to learn about the behavior of the suprabells.

How Does Pitch Move Through a Hole?
 

Image by John Mainstone, University of Queensland, under CC BY-SA 3.0 license

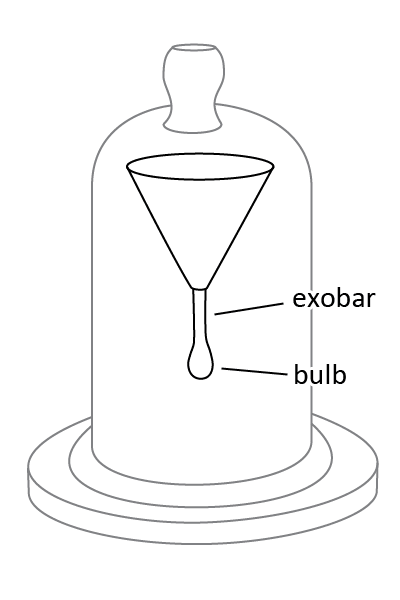The University of Queensland has been performing a long-term experiment that started in 1927 and is still ongoing on this day, which is known as the pitch drop experiment. Its purpose is to measure the flow of a piece of pitch over many years. A heated sample of pitch was poured into a sealed funnel and allowed to settle for three years. In 1930, the seal at the neck of the funnel was cut, allowing the pitch to start flowing. It takes about a decade for a single large droplet to form and fall.

The shape of the expelling fluid resembles the shape of an exobar with a bulb at one of its ends. Even before you've seen this example you could have already suspected that the exobar is the state of equilibrium for a high viscosity fluid, because of its shape and how it resembles a thick sticky fluid that slowly drips down. A fluid that shows this characteristic is pitch.

The exobar is an outer bridge, this means that we now have found the first material whose state of equilibrium is an outer bridge. This is also the first material that is sticky. This property, as you will see in some other organic materials, is a direct result of the state of equilibrium coming from that class of vortices. All materials whose state of equilibrium is an outer bridge are sticky.

Finding all the Patterns

So lets sum things up and express what we have learned so far. Every material is linked to at least one of the vortices in the transformation sequence. The characteristics of that material are a consequence of the characteristics of that material. This vortex is called the state of equilibrium for that material. Even when there are no vortices at all within a volume of that material, then the volume that is uniform still behaves like that vortex. When the material starts to move, and vortices do form within that material, then the movement starts at the position in the transformation sequence where that vortex is located, and thus the first vortices that form in that material are the neighboring vortices of the vortex that forms the state of equilibrium.

Not all materials have one state of equilibrium. Some materials have two or more. The characteristics of those materials are determined by the movement of multiple types of vortices. One such example are metals. If a metal is a pure metal made of only one type of atom, then the metal has not merely one state of equilibrium, but it has more states of equilibrium simultaneously. Its properties are defined by different states, different vortices simultaneously. It is to be expected that all materials that are only made of only one type of atom have more than one state of equilibrium. And it is to be expected that all materials that have only one state of equilibrium are made of multiple type of atoms. Although there might be one or more exceptions to this rule, that has not been determined yet.

Another example of materials that have more than one state of equilibrium are all organic materials. It takes more time and effort to determine the correct states of equilibrium for organic materials, because of their more complex composition. A fine example of an organic material with more than one state of equilibrium is wood. By applying the methods presented on this page on that material, we find different possible states of equilibrium. There are different tools for penetrating wood that are widely used. The nail, the screw, the handsaw and the circle saw. Thus these relate to different types of vortex movement that could all be valid simultaneously. But still you need to be cautious about that some tools are less effective than others, sometimes a tool might relate to a vortex movement close to that of a correct state of equilibrium, an adjacent vortex, which can also be more or less effective but not be the correct state of equilibrium.

There are four simple methods we've found so far that can help us determine the state of equilibrium for any given substance. These methods are:

1. Determine which vortex type is always absent within that substance.
2. Determine what is the shape of least resistance in that substance.
3. Determine how the substance behaves when it is pushed through a hole.
4. Determine what shape the substance adopts when it starts to oscillate.
5. Closely observe how the fluid moves, which vortex does it resemble most?

There are a few comments I need to add here. The vortex that is always absent within a fluid is the state of equilibrium for that fluid. By this I mean that the vortex can not appear completely submerged within that fluid, it can however appear within that fluid on the edge of that fluid when surrounded by another medium. For example, a swirl can not appear underwater, but it can appear at the edge of the water (whirlpool), where there is a transition between water and air. Same as with pitch. An exobar can not appear completely submerged in pitch, but it can appear when a drop of pitch is surrounded by air.

Observing how a fluid moves is another way of determining which vortex is its state of equilibrium. This is best possible with gases or liquids. But you can do the same with solids by looking at the surface pattern, texture and how it breaks or deforms under stress.

The spire is the state of equilibrium of crystal. Crystal, when at rest, behaves like one big spire. Thus a spire vortex is never observed in crystal with one exception being when crystal starts to oscillate.

The disc is the state of equilibrium of metal. Metal, when at rest, behaves like one big disc. Thus a disc vortex is never observed in metal with one exception being when metal starts to oscillate.

The helicone is the state of equilibrium of earth. Earth, when at rest, behaves like one big helicone. Thus a helicone vortex is never observed in earth with one exception being when earth starts to oscillate.

The swirl is the equilibrium of water. Water, when at rest, behaves like one big swirl. Thus a swirl vortex is never observed in water with one exception being when water starts to oscillate.

The amplicone is the state of equilibrium of dust. Dust, when at rest, behaves like one big amplicone. Thus an amplicone vortex is never observed in dust with one exception being when dust starts to oscillate.

The bulb is the state of equilibrium of air. Air, when at rest, behaves like one big bulb. Thus a bulb vortex is never observed in air with one exception being when air starts to oscillate.

The revolute is the state of equilibrium for the outer space medium at a macrocyclic scale. The outer space, when at rest, behaves like one big revolute. Thus a revolute vortex is never observed in outer space with one exception being when the outer space starts to oscillate.

This also implies that:

The shape of least resistance for crystal is a sharp cone.
The shape of least resistance for metal is the flat rotating disc.
The shape of least resistance for earth is a helixoidal cone or cylinder.
The shape of least resistance for water is a voluminous spiral.
The shape of least resistance for dust is a cone shape whose slope growths exponentially.
The shape of least resistance for air is a teardrop shape.
The shape of least resistance for the outer space medium is a thick revolving torus.

And then there are a lot more of these states of equilibrium that need to be found....

Patterns in Material Properties

By finding more states of equilibria, and thus which materials are linked to which vortices, we gradually are able to find more patterns. Note that not all what comes next is explained on this page, for some of it you'll find the explanation on other pages. By comparing material characteristics we are able to find the following links:

1. All substances of which the state of equilibrium is an outer bridge or a tunnel are sticky substances.
2. All substances of which the state of equilibrium is an inner bridge are the opposite of sticky if their position is above the central balance point, and have a granular composition when their position is below the central balance point.
3. All substances of which the state of equilibrium is a spiral are transparent substances.
4. All substances of which the state of equilibrium is a ladder are non-transparent substances, except for the highest and lowest dimensional ladder, at the zero point and the infinity ring.
5. All substances of which the state of equilibrium is a high bridge are combustible fuels.

And this is what we can say about the transformation sequence:

1. The first half-cycle belongs to the minerals and atmospheric gases
2. The third half-cycle belongs to the metals, vapors and partial vacuums
3. The fifth half-cycle belongs to the superfluids and high vacuums

These patterns should help us find even more states of equilibria, and help us in classifying every single material that exists. There are many more of these patterns to be found. What is explained on this page are the basics that form the start of the whole classification system.

Yes but... I thought that matter was made of very small particles!?

That is still true, these new findings do not change that. But instead of only looking at what a material is on a very small scale level, we should also be looking at what it is on a much larger scale, the scale sizes that we are able to see with our eyes. Both the microcyclic scale level and the mesocyclic scale level are essential for our understanding of the universe. And there is a strong correlation between the mesocyclic scale and the microcyclic scale. The question where it comes down to is: what exactly are particles? There is more to be said about this and you can read that on the page about temperature.

Water Thread Experiment

The water thread experiment is a phenomenon that occurs when two containers of deionized water, placed on an insulator, are connected by a thread, then a high-voltage positive electric charge is applied to one container, and a negative charge to the other. At a critical voltage, an unsupported water liquid bridge is formed between the containers, which will remain even when they are separated. The phenomenon was first reported in 1893 in a public lecture by the British Engineer William Armstrong [text from Wikipedia].

When I first saw this floating water bridge the first thing that came to my mind was the troth. The troth is the bridge vortex that connects two swirl spirals, one left turning, the other right turning. We have just learned that water is one big swirl. So when this water is at rest we can consider that its behavior is like that of a swirl vortex. On each side of this bridge is a container with water, thus on each side there is an equivalent of a swirl.

But if it is true that this bridge is indeed a troth, then the water in both of the containers must be different. So just a short moment after the troth first came to my mind I said to myself that either I must be wrong and this is not a troth, or both of the contents of water containers are indeed different. Only then I read that a negative charge is applied to one container and a positive charge is applied to the other. I knew it was not likely that this is a coincidence. The positive and negative charge relates to the left-turning and the right-turning side of the sequence. (I will assume that the left-turning side is positive and the right-turning side is negative, but this is just a choice of convention I'll use for now). The floating water bridge is indeed a troth vortex.

The good news is that this floating water bridge allows us the opportunity to closely study the troth vortex. One of the things we still need to figure out for all of the bridge vortices is the number of movements and the directional path of those movements (the meridians). When small tracer particles (5µm) are added, a high speed visualization reveals a helical flow on the outer layer of the floating water bridge, as you can see in the video below.