Scale Level Interaction

Action and Reaction of Movement

For every action there is an equivalent opposite reaction. When a visible vortex forms at the mesocyclic scale level, that vortex constitutes a visible action. The expectation would be that that movement is counter-balanced by a reactive movement. Yet we do not always see a reactive movement. It can be that we only see one vortex form within one medium, without any other visible vortices. we have seen many examples of that already.

The reason that no reactive movement can be seen is that the reaction takes place on a non-visible scale level, which is the microcyclic scale level. Here the reactive vortices do form, in many numbers to counter-balance the much larger vortex that made the action movement. But these vortices are too small to be seen with the naked eye. If they are not too small they might be seen with a microscope.

The reactive movement that takes place on the microcyclic scale level is both in opposite direction and perpendicular to the movement of action. In the case where a outward movement is made (expansion), this movement is counterbalanced by an inward movement (contraction). If the action movement is a movement that can be described by two dimensions (two axes), then the reactive movement can be described by a single dimension (one axis). Yet both the action and reaction take place on a different scale level.

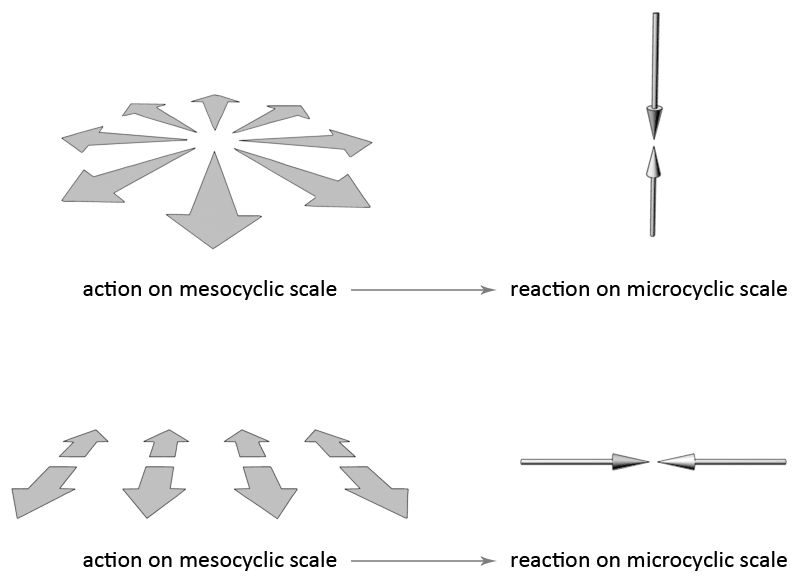
When the movement of action is the formation of a vortex of one particular type, the reaction that takes place is the formation of a vortex that is one of the antipodes of the other vortex. Two vortices that are antipodes of one another have perpendicular movements to one another. And the normal direction of movement of both vortices is also opposite to one another. For example, the revolute is an antipode of the swirl. The revolute makes a flow movement towards the higher dimensions, while the swirl makes a flow movement towards the lower dimensions. Both movements are also perpendicular to one another.

The reactive vortices that form all reside within the volume of the vortex that made the action movement, and their numbers, because of their much smaller size, are in the billions. These vortices can not be seen when they form in the microcyclic scale level. But this same type of action-reaction can also occur in the macrocyclic vs the mesocyclic scale levels, or in a macrocyclic scale level vs a larger macrocyclic scale level. There are situations where the reactive vortices are visible to the naked eye or visible through the lens of a telescope. One such example are the star formations within a spiral galaxy.

It is not certain if these scale level reactions always occur in every situation. It is not certain if the action on the mesocyclic scale always creates a reaction on the microcyclic scale. The reaction on the microcyclic scale might occur because a reaction on the same scale level as where the action takes place is not possible under some, but not all conditions. There might be situations where a different type of reactive movement takes place, on the same scale level, with the same sum result of forces. Or... the reaction on the microcyclic scale only takes place when a reactive movement is possible at that scale level. Here again there might be situations where a reactive movement can not take place at the microcyclic scale level, therefore the reaction can only take place at the mesocyclic scale level. Among the factors that prohibit a reaction are temperature and pressure, whose change of magnitude can be limited by the current temperature and pressure of the environment.

Action and Reaction of Velocity

Contraction as a reaction to expansion, or expansion as a reaction to contraction can also be observed in the speed of movement. When a vortex is higher dimensional, the flow movement of that vortex is slower. When a vortex is lower dimensional, then the flow movement of that vortex is faster. This rule applies to the macrocyclic, mesocyclic and microcyclic scale level. In many situations we can see with our own eyes how fast things move at the mesocyclic scale level, but we can not see how fast things move at the microcyclic scale level. Yet there is a way to perceive how fast things move at the microcyclic scale level even without optical means. When the molecules of a substance vibrate faster, then the temperature of that substance is higher. When the molecules vibrate slower, the temperature is lower. A temperature of near zero Kelvin indicates that the movement of the molecules has come to a near standstill. A very high temperature means that the molecules move very fast. Fast movement is low dimensional, while slow movement is high dimensional. Temperature is thus an indicator of the speed of movement at the small scale level, the scale level that we are not able to see with our eyes.

When the speed of movement increases at the mesocyclic scale level, then the speed of movement decreases at the microcyclic scale level, and thus temperature drops. When the speed of movement decreases at the mesocyclic scale level, then the speed of movement increases at the microcyclic scale level, and thus temperature goes up. This same action-reaction in terms of speed also applies to the macrocyclic vs mesocyclic scale level, yet here it is not temperature that acts as an indicator to the speed of movement in any of these two scale levels.

One example of a decrease in dimensionality at the mesolevel resulting in an increase in dimensionality at the microlevel, thus a decrease in temperature, is a wind fan. A wind fan produces a helibar vortex that is lower dimensional (1.75D) than the state of equilibrium for the air at sea-level, which is the bulb (3.0D). This difference results in a decrease in dimensionality in the air when the movement of that air changes from its moderately slow bulb state to the faster state of the helibar. The rotational helibar vortex slows down the air molecules at the microlevel because they counter-react to seek balance. Speeding up the fan might not lower further down temperature because the vortex type produced is still the same but the speeding up does help to evaporate sweat because of the increase of air flow.

Why do Rocks Move so Slow, yet so Fast?

Rocks are low dimensional. The state of equilibrium for rock minerals is the monolith, which is located close to the lower end of the first cycle within the transformation sequence. Low dimensionality is associated with fast movement, which should be one of the main characteristics of rocks. Yet many people might tend to say that rocks do not move fast, it even appears so that rocks are static. The static characteristic of rocks is actually one that is caused by a different property of low dimensionality, and that property is insensitivity. High dimensional fluids are very sensitive, meaning that once you push against it with your hands, or with a sturdy object, it immediately reacts with movement. When we push against a rock, or twist it, it does not move at all, which is caused by its high degree of insensitivity. But when we twist the rock with a tremendous force, it will at some point break. It will break and form a crack with tremendous speed, like the speed of lightning. So rock does not appear to move because of one particular characteristic, but once it starts moving, it moves tremendously fast, because of that other characteristic.

But how about the tectonic plates then? The layers within the earth, which are moving as we speak, move with a speed that is between 10 and 40 millimeter per year. So here we can say that rocks do move slowly, which appears to be contradictive to the fast movement that its low dimensionality suggests. The answer to this is the scale at which this movement takes place, which is called plate tectonics, is about movement on the macrocyclic scale. The movement that we described by twisting the rock by hand is a movement on the mesocyclic scale. The mesocyclic scale is where the fast movement of the rock takes place, meaning that the rock is low dimensional on the mesocyclic scale level. The macrocyclic scale is where the slow movement of the rock takes place, meaning that the rock is high dimensional on the macrocyclic scale level.

This suggests that the rock is also high dimensional on the microcyclic scale level. The logic is that when something is high dimensional at a large scale level, then it must be low dimensional at a lower scale level, and then it must also be high dimensional at yet a lower scale level. Thus from high to low to high etc. Yet here we need to be cautious about jumping to conclusions, because rocks that reside far beneath the surface of the earth are subjected to high pressure. Under conditions of high pressure or high tension it is possible for something to be both low dimensional on one scale level and low dimensional on the next scale level as well, or to be both high dimensional.

What is interesting to mention is that when we heat rock to very high temperatures, to the point that it melts, then these three different states within the three different successive scale levels will all three have changed into their opposite. High to low to high will change into low to high to low. The rock will now be higher dimensional on the mesocyclic scale level, that is why we see the rock, which is now lava, to move slowly instead of move at lightning speed. We no longer require to use tremendous force to make the rock move, instead lava can be moved around by a sturdy object quite easily because it has lost its insensitivity property. It even starts flowing by itself. The lava now moves faster deep within the earth then it does as a tectonic plate, because it is now lower dimensional on a macrocyclic scale, meaning that its speed of movement is now faster at the larger scale. The high temperatures indicates that the movement at the very small level, the vibration of the molecules, has increased, which tells us that the rock has become low dimensional on the microcyclic scale level.

Progressive Scale Level Reactions

When an action at one scale level takes place, a reaction at the next smaller scale level will occur. But the reaction will not end at this next scale level. At an even smaller scale level the reaction will proceed, and possibly the reaction will also proceed to progress into the next smaller scale levels. Each scale level on which the reaction takes place is at least thousands of times smaller than the previous scale level at which the action occurred. If the first action is a high dimensional movement, then the reaction that follows will be a low dimensional movement. The next reaction will again be a high dimensional movement, which then again is proceeded by a low dimensional movement. This alternation between expansion and contraction can be interpreted by a sine curve, as the one illustrated in the image below.

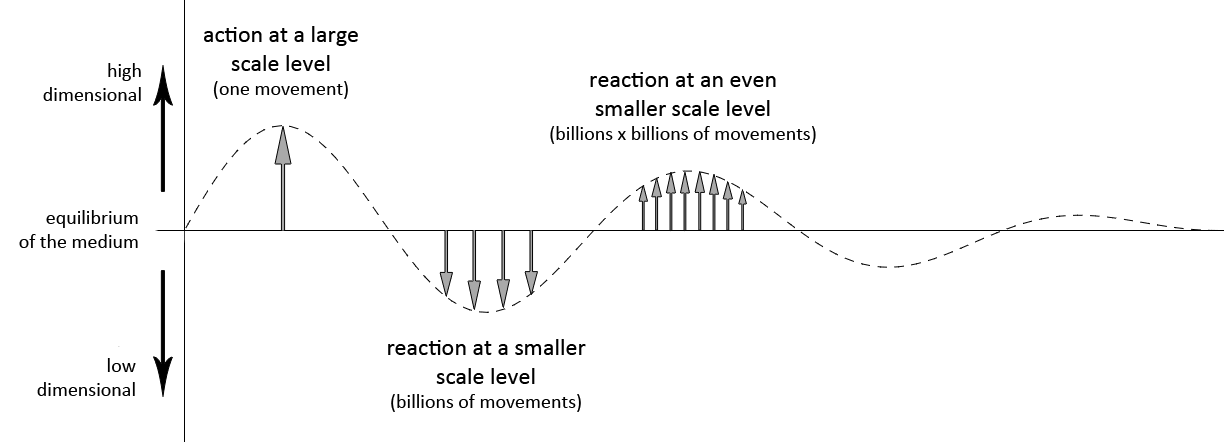
It is likely that the magnitude of the reaction in each next scale level is a reduced sum of the reaction in the previous scale level. The magnitude should gradually fade to zero as the forces progress to lower and lower scale levels. It should fade to zero otherwise the reactions would continue endlessly into the deeper and deeper scale levels. But this assumption is based on logic and not on observation, it is therefore not certain. In the graph above I have illustrated this by lowering the amplitude of the sine curve from left to right, thus from large scale to small scale. Eventually the sine curve merges with the equilibrium when it attains zero amplitude.

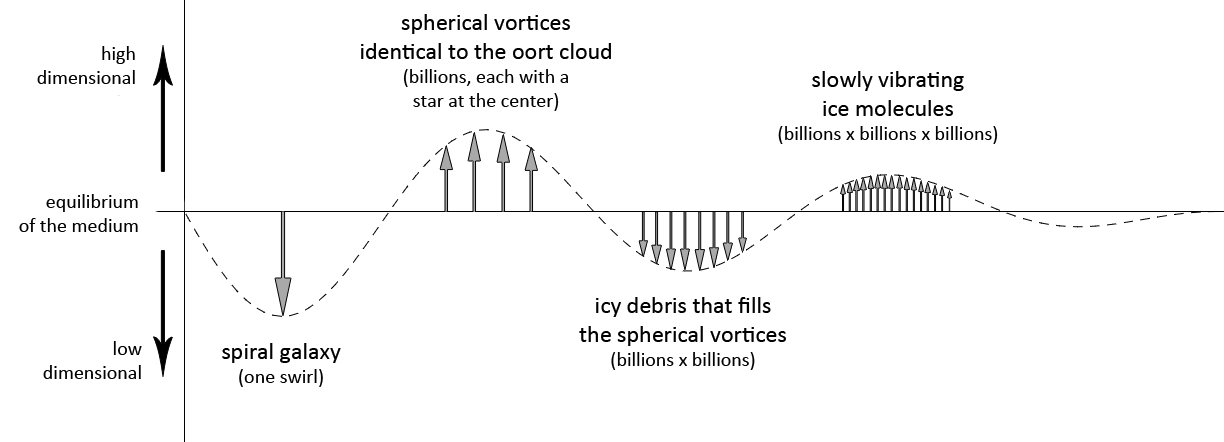
One example of progressive scale level reactions are the spiral galaxies with their star formations. The stars itself are not the direct reaction to the formation and movement of the spiral (swirl) that we call the Milky Way. The reaction to the swirl could quite likely be the Oort cloud and many other spherical vortices identical to the Oort cloud, residing within the Milky Way spiral. The Oort cloud is a cloud consisting of mostly icy debris believed to surround the Sun to as far as somewhere between 50.000 and 200.000 AU (0,8 and 3,2 light years). This spherical vortex should be a high dimensional vortex, that might be rotational or non-rotational, which could be a bubble or some other type of orb. The icy rocks are low dimensional, this because ice is a crystal and crystalline structures are low dimensional. The low temperature of ice tells us that the ice molecules vibrate relatively very slowly, and slow movement is high dimensional. Thus in this example we can find how the reaction alternates between a high dimensional movement and a low dimensional movement as we zoom in further and further into our galaxy.
 

If it is not the Oort cloud that is the counter-reaction to the Milky Way swirl, then the next possibility would be the Kuiper belt. But the Kuiper belt, whose vortex type is either the mercury belt or a vortex type close in the sequence to the mercury belt, is a less likely candidate for this counter-reaction because although the mercury belt is a vortex from the third half-cycle and thus higher dimensional than the swirl, it is not an antipode of the swirl, therefore less likely to be the vortex that counter-balances the movement of the swirl.

Sonoluminescence

Sonoluminescence is a phenomenon at which tiny burst of light can occur at the center of a water bubble when that water bubble implodes under the influence of ultrasound. For this it is required that the sound wave is of sufficient intensity, and the bubble has to be located at the location where the amplitude of the standing wave is the maximum (at the anti-node of the wave). Sonoluminescence in the laboratory can be set up to repeat itself in a stable manner, so that a single bubble will expand and collapse over and over again over time, emitting a burst of light at each interval when a new bubble collapses. The light flashes from the bubbles are extremely short, between 35 and a few hundred picoseconds. Measurements have shown that the temperature within the bubble ranges from 2300 K to 5100 K at the moment that the bubble collapses.

Image by Dake (Wikimedia), under CC BY-SA 3.0 license

It is possible that the existence of our sun is caused by a collapsing bubble-like vortex, the bubble which we call the Oort cloud, just as the tiny burst of light in the laboratory set-up is caused by the imploding water bubble. But it is more likely that the Oort cloud is slowly contracting and not collapsing, and thereby creating the same light effect, yet smaller and less brightly, at the center of the bubble. This gradual contraction of the Oort cloud is caused by the spiraling movement within the much larger spiral galaxy towards the center of the galaxy. A quick collapse of the bubble would create a short-lived yet far more brighter light phenomenon like a quasar. 

While a quick collapse of a bubble causing a short burst of light has been achieved in laboratory experiments, a gradual contraction of a bubble under influence of a larger vortex (or some other mechanism) has not yet been achieved. This might be the key in successfully creating a stable light source that more closely enables us to understand how our sun or any other star is 'pushed' to emit its light.

Can the Mesocyclic Affect the Macrocyclic?

At this point you would think that this interaction, which can produce a reaction effect from a mesocyclic vortex on the microcyclic scale level, can not produce a reaction effect from a single vortex the other way around, thus a single vortex of a mesocyclic size that produces a reaction effect on the macrocyclic scale. It is possible that a change on the microcyclic scale gives a reaction on the mesocyclic scale, but that change can not be induced merely by one single vortex. The effect at the larger scale level can be established by the motion of many small vortices within a volume of matter that is very large in respect to the small scale level at which the movement is initiated. Such an action and reactional movement can for example be established through a chemical reaction, such as the mixing of two liquids.
 

However, there is one phenomenon that suggests that a reaction at a larger scale level as a result of just one single vortex movement at a smaller scale level does might happen. And that phenomenon is velocity time dilation. The faster an object moves, the slower time runs for that object. This principle has been described by Einstein's theory of relativity. The velocity of time is an effect of the macrocyclic scale level, an effect which in this case, when the object accelerates in a straight line, is caused by an object mimicking (and thereby inducing) the movement of a spire at the mesocyclic level.

The logical though behind this is that when an object becomes lower dimensional on the mesocyclic scale, in this case by speeding up, the object does become higher dimensional on the macrocyclic scale, although the object itself is much smaller than everything that belongs to the macrocyclic scale. But the reason that this happens is probably not because the macrocyclic scale is truly affected by the object in the mesocyclic scale, but more likely because the object, by speeding up, breaks away from the macrocyclic vortex in which it resides, and as an effect of that it more and more starts to reside within the larger dimensional space in which the macrocyclic vortex itself resides. Larger space, or larger vortices, is higher dimensional, thus slower progression of time. This explanation is a theoretical possibility but one that is not certain while there can also be one other explanation for the phenomenon of time dilation. More about this will be explained on the second-last page, which is the page about time.