Waves and Projection

Amplitude

When a wave only increases in frequency, without any change in amplitude, then the difference between these waves is a difference in dimensionality in terms of dimension levels. Low frequency means a low dimension level, thus a low number of axes (low number usually means less than three axes). A high frequency means a high dimension level, thus a high number of axes (high number usually means more than three axes).

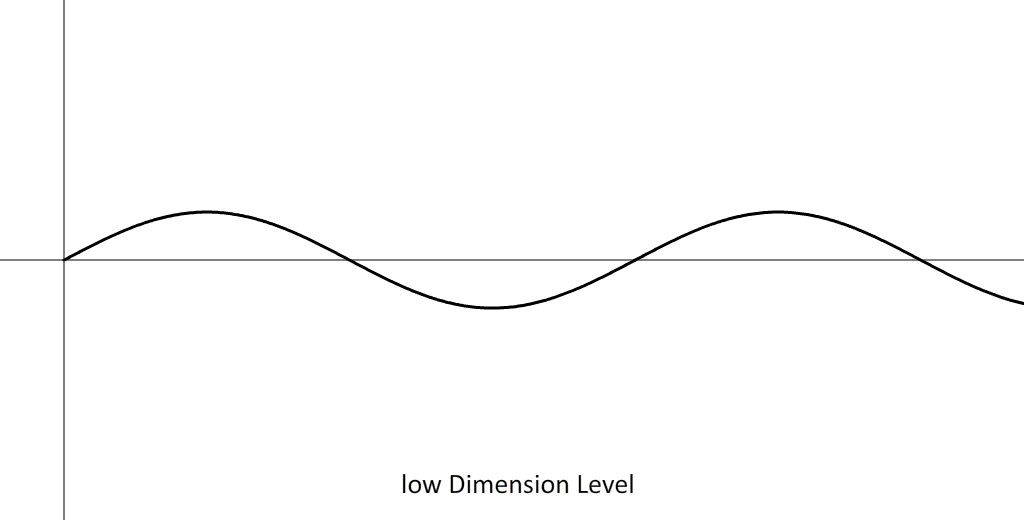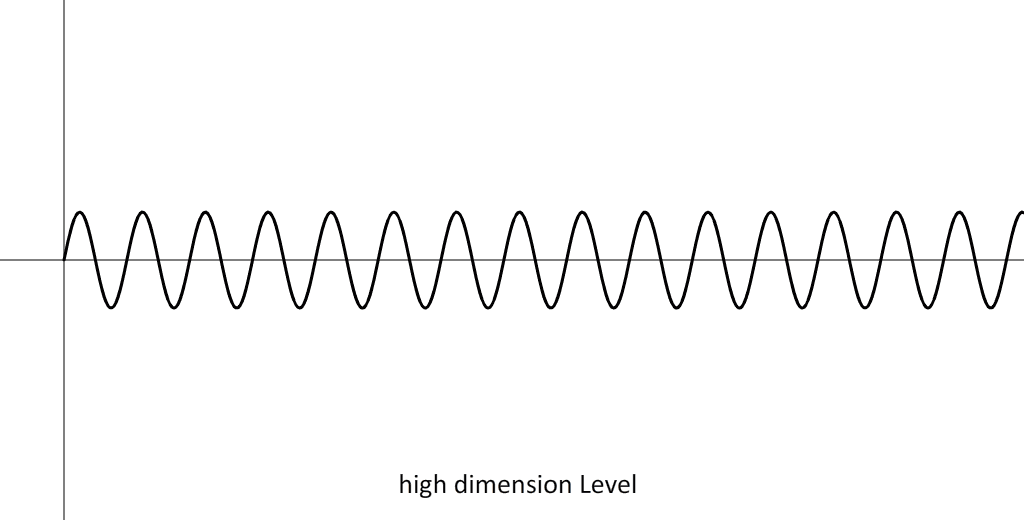
The amplitude of a wave determines the scale size of a wave. In the example above both waves exist within the same scale size, thus an equal largeness of the waves. This is because the amplitudes of both waves are the same. When the amplitude of a wave is larger than the scale size of the wave is also larger. The visual effect to us is that the vortices that connect to these waves are also larger by an equal magnitude.

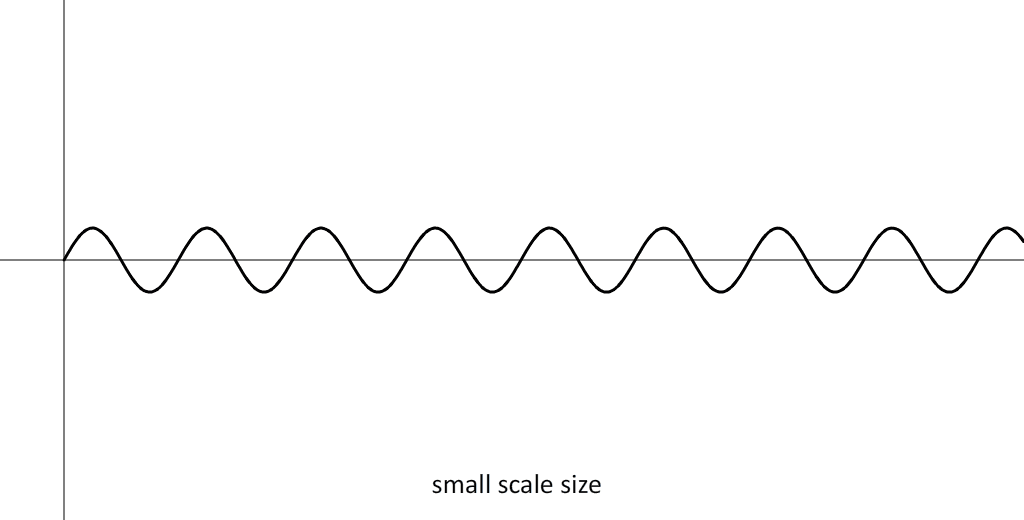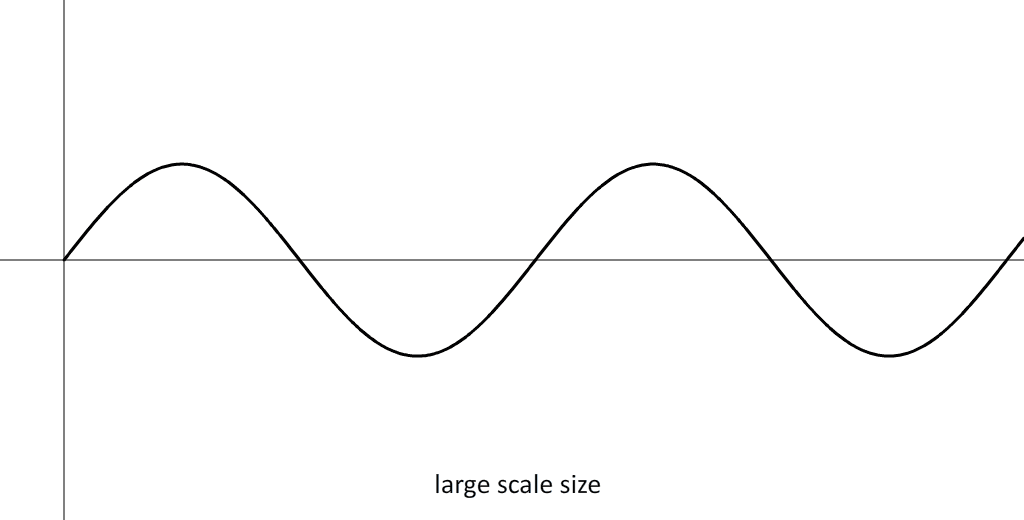
The relation between wave amplitude and scale size reveals to us why vortices that morph sequentially always increase in size when morphing. This is a logical consequence if the wave only increases in amplitude without a change in wavelength. The resulting new wave is a wave that looks like wave with a shorter wavelength, but it is not a wave with a shorter wavelength because the scale size is larger. But it is a wave of a higher dimension level.
 

AMPLITUDE = SCALE SIZE

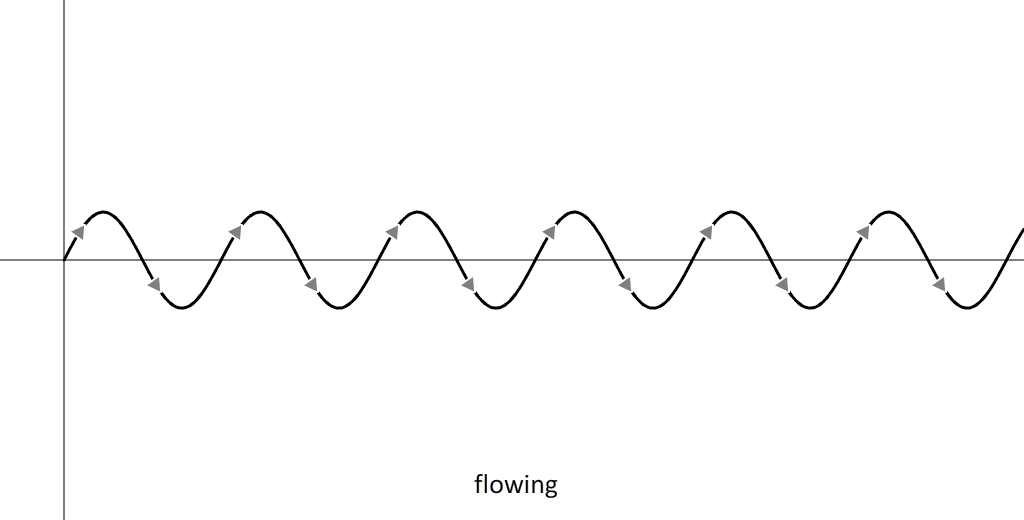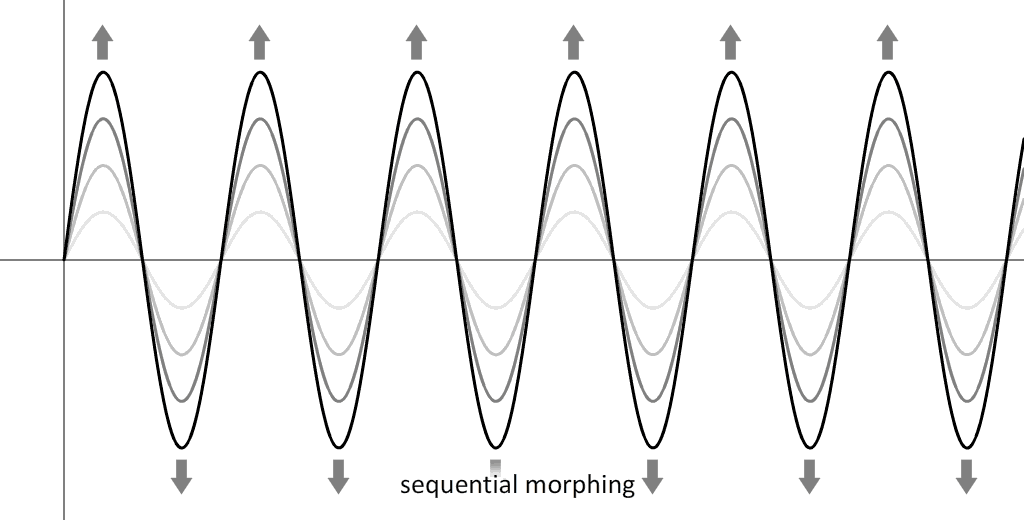
THE REASON THAT VORTICES ALWAYS INCREASE IN SIZE WHEN MORPHING SEQUENTIALLY IS THAT ONLY THE AMPLITUDE OF THE WAVE INCREASES, NOT THE WAVELENGTH

Perhaps it is not possible for a wave to increase in both amplitude and wavelength at the same time. I say that because I haven't seen any observations of vortices that can do that. The visual effect would be that the shape of the vortex would stay almost the same while only the size of vortex would increase. Such a movement rapidly creates enormous tension and can not be completed. Perhaps the only example of a vortex that can do that is a soap bubble being blown up. The one single movement that can successfully move and transform every vortex type towards a larger scale size is sequential morphing.
 

SEQUENTIAL MORPHING = THE PROGRESSIVE CHANGE OF A VORTEX INTO A SUBSEQUENT VORTEX IN THE SEQUENCE THAT IS TWO DIMENSION LEVELS HIGHER OR LOWER. THIS CHANGE HAPPENS DUE TO A CHANGE IN ANGLE OF PROJECTION THAT RESULTS IN AN INCREASE OR DECREASE IN WAVE AMPLITUDE AND A CHANGE OF THE SIZE OF THE VORTEX.

The Projection Method

Flatland: A Romance of Many Dimensions is an 1884 satirical novella by the English schoolmaster Edwin Abbott. Abbott used the fictional two-dimensional world of Flatland to offer pointed observations on the social hierarchy of Victorian culture. However, the novella's today is more know for the way it describes dimensions. In a foreword to one of the many publications of the novella, noted science writer Isaac Asimov described Flatland as "The best introduction one can find into the manner of perceiving dimensions." As such, the novella is still popular amongst mathematics, physics, and computer science students.

Flatland has often been used as an analogy to explain the possibility that we live in a world with more than three dimensions. In flatland there are two different living beings, one that lives in three-dimensional space and sees the world as three-dimensional. The other live in a three dimensional plane, and see only the world within that two-dimensional plane. Yet both live in the same universe. Take a look at the video below. It sort of gives you an idea how the world in flatland behaves.

It should not be hard to imagine why I bring flatland into the picture here. The similarities with how I myself try to simplify the universe in words so that it allows me to explain how it behaves are quite obvious. At the time of writing of this English novella these thoughts about extra dimensions might have been no more than fiction. But nowadays I can say that this flatland analogy is closer to reality than to fiction.

On one of the first pages I showed you a model that describes the projection of the wave field in a simplified way. The difference with that model with flatland is that there is no projection. In flatland, everything that is located outside the plane does not influence the plane, does not touch the plane, and can be considered to be non-existent for any creature that lives inside the plane. In our real universe, a great part of what is located outside in the non-physical realm, does influence the physical realm because a wide range of it is projected towards our space.

You need to imagine our non-physical universe as not a universe with an infinite number of dimensions, but a universe with three dimensions instead. Within this three dimensional universe lies a two dimensional plane. This plane is our physical world, which here is represented as two dimensional instead of three. This two dimensional plane is how we for now assume to perceive the universe that we live in (off-course in reality we perceive the world as three dimensional, for now we omit one axis of movement to explain things in a simplified manner).

The waves are then described as a series of lines, being only one dimensional. The angle of these lines to the physical plane is what describes the dimensionality of the wave. Low angle is low dimensional. High angle is high dimensional.

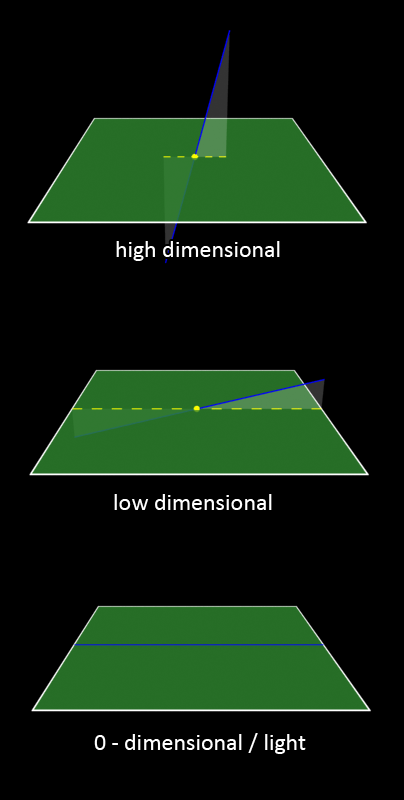
Yet it was already said that this method of describing things is for many things insufficient. Only the basics of projection for the first half-cycle are described this way. High dimensional waves are supposed to be more directional than low dimensional waves. Yet this model is so simple that all waves are completely directional.

Explaining field projection with model #2

The problem with the previous model is that it is too simple to describe the shape of the waves. Waves are not straight lines, waves are to some degree spherical. If these waves are represented within a two dimensional world then a better way to describe them would be by using circles, that radiate outward or inward. So for this I came up with model #2. A method that is a bit less simple, but a bit more accurate.

The image below illustrates the basics of this model. Most of the steps are the same as in the previous model. The non-physical universe is 3D instead of infinite dimensional, our physical world is 2D instead of 3D, and the vortex, also like in the previous model, is depicted as a yellow dot. The difference with the previous model is that instead of using lines to describe waves, we now use the outer surface of a cone to describe the path of a wave.

The outer surface of a cone is the shape that the path of the wave describes. The wave is here no more than a circle that radiates outward from the vortex. When it radiates outward at an angle to the plane then the resulting shape is a cone. Now the projection of this wave onto our physical world forms a circle that radiates outward, which is a more correct way to describe a spherical outward moving wave in a two dimensional world. It is still a simplified way to describe things, but more closer to what it is in reality then with the previous model.

In this model, the steepness of the cone describes the frequency of the wave. A low steepness of the cone means a high frequency, thus high dimensional. A high steepness of the cone means a low frequency, thus low dimensional. Here too light can be described as a vortex that lies completely within the physical plane. This happens when the steepness of the cone is exactly 0 degrees. In that case the cone is no longer a cone, but a flat disc that intersects the physical plane. Electricity is also described adequately. Electricity manifests itself when the steepness of the cone is exactly 90 degrees. When a wave that travels over that path is projected onto the plane, then the result is that there is only a vortex in our physical world, and no wave.

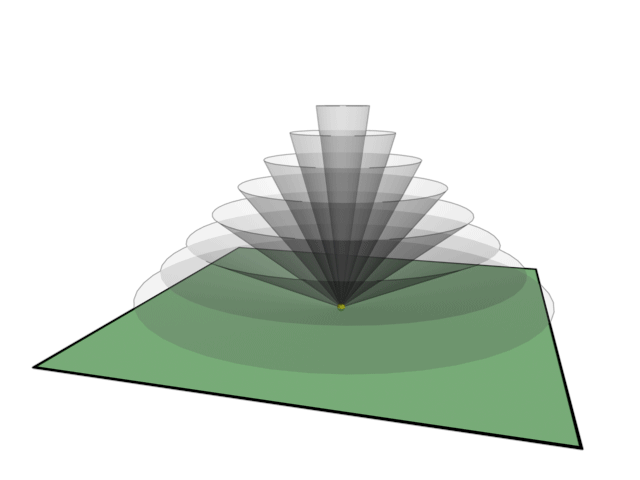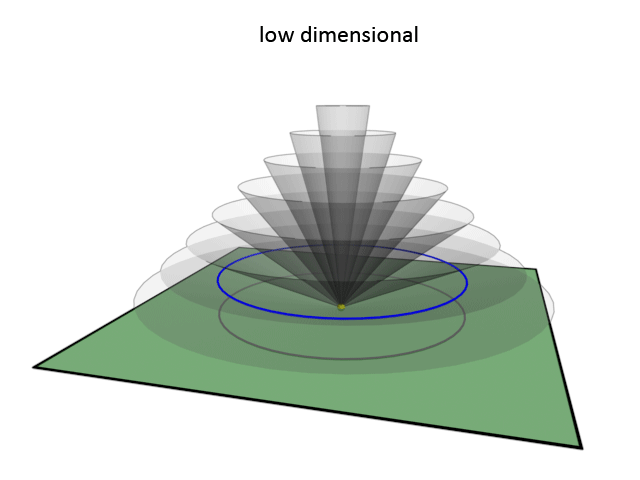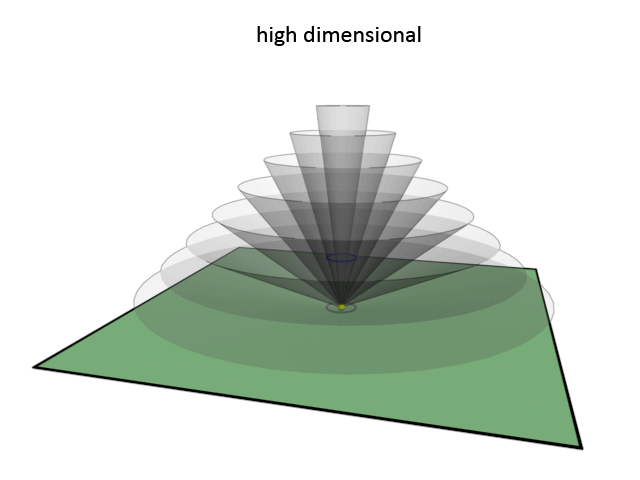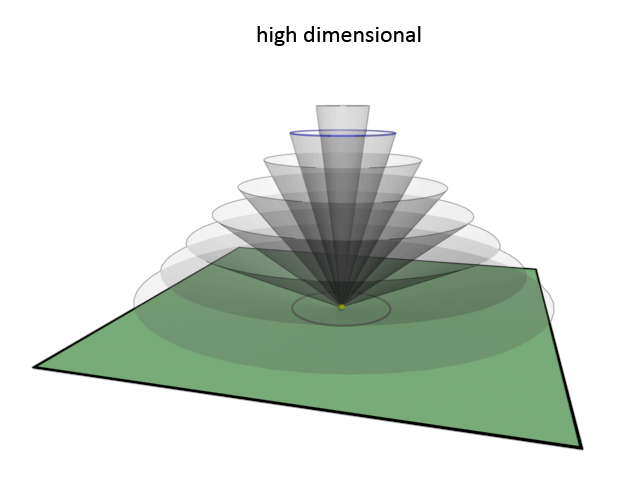
A wave in this model can be more directional by making an angle with the physical plane that deviates from 90 degrees. For this model to describe high and low dimensionality correctly the cone should never be oriented in such a way that it crosses the physical plane. It can fully intersect the plane (which would make it no longer a cone), or it exists only at one side of the plane. The consequence of this is that a low dimensional wave always radiates in nearly the same directions, because there is very little option as to how to orient the cone. The high dimensional waves can be oriented in many ways, thus being pointed in many possible directions, because of the steepness of the cone and the possibility to orient the cone at many possible angles.

It won't take long for someone to come to the conclusion that this model, like the previous simpler model, still does not describe many of the characteristics that we would expect of high and low dimensionality and contraction and expansion. This model is still too simple. We yet again need to come up with a better way to describe how the projection works. But for now the two models that have been presented are sufficient to explain the basics of how the projection from an infinite number of dimensions to no more than three dimensions works.

So in at least one point this model is better than the previous model. This model describes the wave better. In one aspect you could say that this model is less than the previous model, because it is somewhat less simple. The most simple models are often the best to describe things.

The Projection is Perceptual, not Physical

The universe that we live in can be described as the universe that exists before the projection and after the projection. The universe before the projection has an infinite number of dimensions, that are likely to be all distributed uniformly, without any regions overlapping. The universe after the projection has only three dimensions, that are formed by projectively merging of up to a large number of dimensions.

The words 'before' and 'after' suggest that the process includes a factor time. It suggests that the projection is a physical process that takes time to fulfill, while in fact it does not. The projection is not physical, nor does the projection take any time to accomplish. The projection is not physical, because it is only visual, the projection does not take place in the universe that we life in, it takes place by our eyes. Our visual organ, in conjunction with all our other senses, are what creates the perception of a three dimensional universe. It is not like there is a movie projector in the room that projects something onto a screen in the room, instead it is only us who put on a pair of special glasses, glasses that instantly give us a different view of the environment.

If we humans would be a different type of life-form, one with a much different visual perception of the environment, then the cameras that we would build to capture images would look a lot different than the cameras that we use in this life. The light in which the camera would capture an image would be a different type of wave, one that possibly would not classify as light to us in this life. The zero point would be at a different location, so would be the infinity ring, and so would all other EM crossing locations. We mimic the way that our eyes work when we build a camera, the camera gives an image that is close to the same result as our eyes give to us.

I know this is something that will be hard for me to pass on to people. I am aware that it won't be that easy for me to convince people that this is true. But I know very sure this is true. There is a margin for error in the infinity theory, I can surely make mistakes here and there that will need to be corrected later. But of this I'm very sure that this is true. Yet this might be among that which is most difficult to convince human beings of.

The Hopf Fibration

The best way to come to a better model to describe how the field projection works is to first know the exact method as to how the field, and thus the waves that propagate through that field are projected. And for that our knowledge as to how this projection works would be most complete if we knew how to describe this method accurately with one equation, or a unification of multiple equations. Until now, mathematics has not been introduced on this website, only mentioned on a few occasions. Reason for this is that I'm not a mathematician, it is not my calling to write many details about math. Yet I am aware of the significance of math, and I do embrace its evolution and its application. One possible step to getting closer to describing the transformation sequence with an equation is a mathematical object called the Hopf fibration.

Image by Niles Johnson, under CC BY-SA 3.0, license.
Part of image was removed and cropped.

The Hopf fibration, named after Heinz Hopf who studied it in a 1931 paper, is an important object in mathematics and physics. It was a landmark discovery in topology and is a fundamental object in the theory of Lie groups. In the mathematical field of topology, the Hopf fibration (also known as the Hopf bundle or Hopf map) describes a 3-sphere (a hypersphere in four-dimensional space) in terms of circles and an ordinary sphere. The Hopf fibration has a wide variety of physical applications including magnetic monopoles, rigid body mechanics and quantum information theory (Text from David W. Lyons and Wikipedia).

One of the higher dimensional vortices in the first half-cycle is the revolute. There seems to be a strong connection between a topological object called the Hopf fibration, and the revolute vortex. The Hopf fibration consists of a collection of circles that form tori. But none of the circles from any of the tori ever intersect one another. Yet these different circles form complex shapes that even with the addition of thousands of circles to the same space does not result in any collision between the paths of these circles. The video below, which originates from the Dimensions Website, gives an introduction to this topological object.

The revolute vortex is also a vortex that is shaped like a torus. The paths of these different circles are somewhat similar to the paths of the meridians (the individual movements of a vortex). Meridians are also paths that never intersect, even when the number and density of these movements is large. The difference between the two is that these paths are looping, while in the revolute the meridians are not looping. The different tori of the Hopf bundle should progress into a spiral, instead of being different layers with different radii. If the equations for the Hopf fibration can be altered in a way that the topological object forms a spiral, then this might be one significant step towards finding the correct equation for the entire transformation sequence. Such an equation could then show us the shape of the vortices, and the paths of the individual movements, the meridians.

The equation for the Hopf fibration requires complex numbers (numbers that include an imaginary unit). The one dimensional axes that describe the space in which the Hopf fibration is drawn are replaced by two dimensional planes. On the next page I will talk about the Schrödinger equation, which is on this website explained to be a puzzle piece for understanding vortex shapes. The Schrödinger equation also requires complex numbers with an imaginary unit. Changes are high that solving the mathematical puzzle of the transformation sequence requires the knowledge and application of complex numbers.