Tension and Compression
This page focuses on two opposite forces, tension and compression, and explains how these two forces come about. Both of these forces are caused by a vortex making a wrong move. For example by a spiral not spiraling inward but continuing in a straight line, or any other vortex which sum movement goes in the wrong direction. Tension occurs when a vortex makes a wrong move while it makes an expanding flow movement that progresses towards the next vortex within the higher dimensions. Compression occurs when a vortex makes a wrong move while it makes a contracting flow movement that progresses towards the previous vortex in the lower dimensions.
It is only when a vortex makes the correct move that the number of meridians (individual movements) inside the vortex can progressively increase or decrease and thus dimensionality correctly increase (become more yin) or decrease (become more yang). The number of meridians do not decrease when a vortex is contracting in the wrong direction, instead a compressive force builds up due to the now too many paths of movement beings squeezed into too little space. And the number of meridians do not increase when a vortex is expanding in the wrong direction, instead tension builds up due to too little movements and thus too little freedom of movement being there to complete the move.
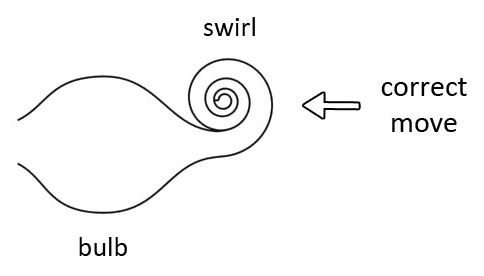
One way of making a wrong move is when a spiral proceeds in a straight line. The end result is what we call an 'unrolled spiral'. The image above shows a very simple spiral being unrolled. That a spiral vortex is unrolled does not mean that it can unroll and re-roll. We find a spiral either in a rolled or unrolled state, but I have found only a few examples of spirals dynamically unrolling in nature, and I'm not sure if those examples were related to vortex movement.
If a ladder is attached to an unrolled spiral at its high end, then tension builds up when the movement goes from the ladder to the spiral. When tension reaches a maximum the movement will come to a standstill and then reverse back from the spiral to the ladder. Same is true when the ladder is attached to an unrolled spiral at its low end. When the movement goes from the ladder to the spiral, a compressive force builds up. When this compressive force reaches a maximum the movement will come to a standstill and reverse back from the spiral to the ladder. The image below shows a ladder, a bulb, that is attached to an unrolled spiral at both ends.
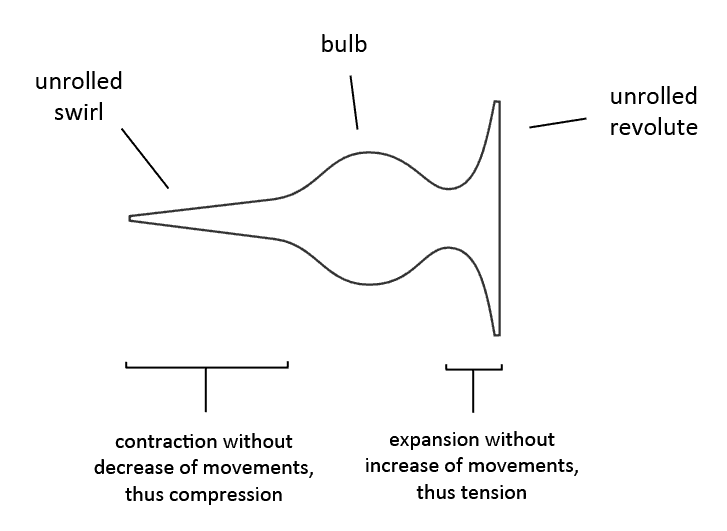
The vortex in the image above I call an 'oscillation bulb'. The high end and low end of this vortex is how a revolute and swirl look like when you unroll them, with the difference that the arms of these unrolled spirals are much shorter than the arms of the rolled up spirals. Only a small distance is needed to build up a significant amount of tension or compression.
IF YOU UNROLL A REVOLUTE, THEN WHAT YOU GET IS SOMETHING THAT ALMOST LOOKS LIKE AN AUREOLE BELT, THE NEXT LADDER IN THE SEQUENCE
IF YOU UNROLL A SWIRL, THEN WHAT YOU GET IS SOMETHING THAT ALMOST LOOKS LIKE A HELICONE, THE PREVIOUS LADDER IN THE SEQUENCE
If you unroll a disc spiral, then what you get is a straight line. If you unroll a swirl, then what you get is a cone. It does not matter in which direction or from which starting point within the spiral you unroll these vortices, the unrolled part will always look like a line or cone. But if you unroll a revolute, the starting point and the direction in which you unwind does matter. If you unroll a revolute from its lowest end then the unrolled part will look like a solid cylinder. If you unroll a revolute after making a 90 degree turn then the unrolled part will look like the brim of a hat (annulus shape). If you unroll a revolute after making a 180 degree turn then the unrolled part will look like a hollow cylinder.
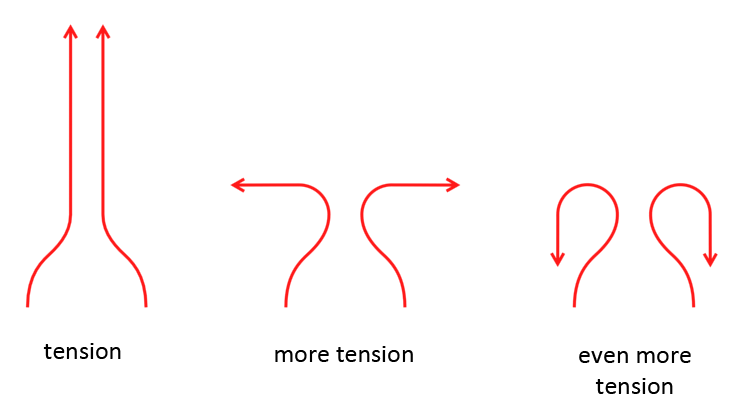
What I think, but of which I must say that I'm not entirely sure, is that the further the point is where you start unrolling, the stronger the tension is that builds up in the vortex. The image above illustrates what I've just described. In the left image, where the tension is the weakest, you need the longest unrolling before the tension is strong enough for the vortex movement to reverse. In the middle image, where tension is stronger, you only need a short unrolled part for the movement to come to a standstill and reverse. In the right image, where tension is even greater, you need no more than a very short unrolled part for the movement to reverse. But this needs to be tested with some simple experiments before we know if this is correct.
Oscillation only takes place when the sum movement reverses at both the high end and the low end of a vortex. In that case the movement starts to go back and forward between compression and tension. More or less like a helical spring that you first give a hard pull and then let go. It goes back and forward until the movement dies out. There are five different examples on this page that illustrate this phenomenon. The first one we will discuss is the oscillation of air inside a Helmholtz resonator.
Example #1 - Helmholtz Resonator
_FromPhysicsCaseWesternReserveUniversity_UnderCCBYSA2.5.jpg)
Image by Red Devil 666 (Wikimedia), under
CC BY-SA 2.5 license
We already briefly mentioned the Helmholtz resonator on the page about state of equilibrium. The Helmholtz resonator, also called the Helmholtz oscillator, is a simple device that can oscillate air inside a cavity. There are two holes in this copper sphere, one larger hole with a short neck and one smaller hole with a longer conical neck. The copper sphere is a bulb. The conical neck at the low end of the bulb (low end is at the top of the image) is an unrolled swirl. There is no unrolled revolute at the high end, only a short neck. The compression in this device is stronger than the tension.
The conical neck at the top of the image also looks like an amplicone. Yet an amplicone starts with a wide radius at its smallest end, and a helicone starts with a pointed tip. Because the radius of the hole in the top of the Helmholtz Resonator is so small, I assume that the effect is more like that of a helicone, or more like the vortex one dimension level higher than the helicone, the unrolled swirl. A shape with such a small hole does not induce the movement of an amplicone.
Example #2 - Static Discharge
Some metal objects can produce a static discharge. A static discharge is the sudden neutralization of an electric charge that has build up on the surface of an object. The effects of static electricity are familiar to most people because we can feel, hear, and even see the spark as the excess charge is neutralized when brought close to a large electrical conductor (for example, human body parts or metal objects). The captured image below shows such an electric discharge. In this example, the build-up of static charge is in a metal doorknob.

As you might have already noticed, the shape of the doorknob is that of a bulb with an unrolled revolute attached to it. There is no unrolled swirl at the other end. This shape produces lots of tension and only little compression because only the first half of the bulb lies underneath the point of equilibrium. This reveals to us that tension is the key force in this metal doorknob and that there is some kind of relation between this static discharge and tension. It is a valuable clue that tells us that a static discharge is caused by a sudden release of tension.
How exactly a too high tension leads to a sudden release of that tension is not known, but it could be compared with pulling on an elastic object until it breaks and the force is released. If you let go of the object before it breaks then the tension will gradually release and the length of the elastic object will fall back to the equilibrium length. If the object breaks then the fallback is more rapid, and here too the length will fall back to its equilibrium length, yet because of the breaking of the object the equilibrium length is a new length.
There is however one more important detail that we can add. One more thing that we know of. And that is while the increase of tension or compression occurs over the positive dimensions, the sudden release of these forces happens over the negative dimensions. Dimensionality suddenly flips from positive to negative. This happens with electricity and lightning, and also with sonic booms which are described a bit further down on this page. So the little spark that you see between the doorknob and the tip of the finger is a negative dimensional vortex. The vortex is made of plasma and all plasma is negative dimensional matter.
STATIC DISCHARGE = SUDDEN RELEASE OF TENSION FROM WITHIN AN ELECTRICALLY CONDUCTING OBJECT IN THE SHAPE OF A VORTEX MADE OF A MATERIAL WHOSE STATE OF EQUILIBRIUM LACKS THE REQUIRED NUMBER OF MERIDIANS. THIS RELEASE ENDS IN A FALLBACK TO THE EQUILIBRIUM IN A DIFFERENT CYCLE
With this example I'm not saying that all static discharges are caused by this same principle. But some are, and it was unknown until now that the shape and geometry of many objects in our environment cause physical effects that can only fully be explained by understanding vortex movement. We are now steps closer at understanding a static discharge. The next example on our list is lightning.
Example #3 - Lightning and Thunderclouds
We are all familiar with lightning. We've seen it, we've heard it. Lightning is an atmospheric discharge of electricity accompanied by thunder, which typically occurs during thunderstorms. How lightning initially forms is still a matter of debate: Scientists have studied root causes ranging from atmospheric perturbations (wind, humidity, friction, and atmospheric pressure) to the impact of solar wind and accumulation of charged solar particles.

One phenomenon that creates lightning are thunderclouds. A thunderclouds are tall and dense clouds. Looking at such a thundercloud, one can see that the shape of the cloud is that of an unrolled revolute. So here again, just as with the doorknob, the electric discharge is caused by a sudden release of tension. The vortex movement goes from the bottom of the cloud upward and outward into the sky. When too much tension has build up dimensionality flips to negative and the movement rapidly falls back to the equilibrium, which in this case is at 3.0D, because the state of equilibrium for air is the bulb. The difference with the doorknob example is that the vortex movement takes place on a much larger scale size and in air instead of metal. Another difference is that with lightning, the shape of the vortex forms due to the weather conditions, while in a static discharge the shape of the vortex is prefabricated in the shape of the object that acts as the electrical conductor.

There is no bulb at the bottom of the thundercloud. If you read all the pages until here, then you also understand why. The bulb is the equilibrium of air. Air already acts like one big bulb and thus a bulb vortex can not be visible in air. (I made a small mistake in this image. It looks like the thundercloud touches the ground, but a thundercloud never touches the ground. Instead it hovers above the ground in a layer of clouds). Now that we know what a static discharge is we can also formulate a definition for lightning.
LIGHTNING = SUDDEN RELEASE OF TENSION FROM WITHIN A VORTEX IN AIR THAT LACKS THE REQUIRED NUMBER OF MERIDIANS. THIS RELEASE ENDS IN A FALLBACK TO THE EQUILIBRIUM IN A DIFFERENT CYCLE.
This example only explains lower atmospheric lighting. There are at least three other types of lighting higher up in the earth's atmosphere. These are called blue jets, sprites and elves. Logic tells us it is almost certain that these types of lighting are also caused by release of tension. We do know that these types of lighting have a shorter lifespan than lower atmospheric lighting, they last only milliseconds. This reveals to us that tension is greater, so the fallback starts higher up in the sequence.
_Edited_UnderCCBYSA3.0.jpg)
Lightning photos were taken from other image by Abestrobi (Wikimedia), under CC BY-SA 3.0 license
These types of lightning are also caused by a vortex making a wrong move. What these possible variants of movement are needs to be found out if we want to be able to reproduce these types of lightning in experiments.
Example #4 - A Bullwhip's Sonic Boom
The next example on our list comes from another man-made object: the bullwhip. A bullwhip's length, flexibility, and tapered design allows it to be thrown in such a way that, toward the end of the throw, it creates a sonic boom. This sonic boom is the familiar cracking noise that we hear from bullwhips. The body of the whip is braided, and made from leather strips (or nylon, in modern variants). This body of the whip, called the thong, is an unrolled ascended disc. Because it is ascended, it shows the characteristics of a swirl. Namely the left and right zig-zagging movements of the meridians. Each strip of leather acts as one individual movement (meridian) of a vortex. As you throw the whip, a force travels from the handle to the other end of the whip. This force creates a vortex movement through the highmorph disc that is contractive, thus traveling from the higher dimensions to the lower dimensions.
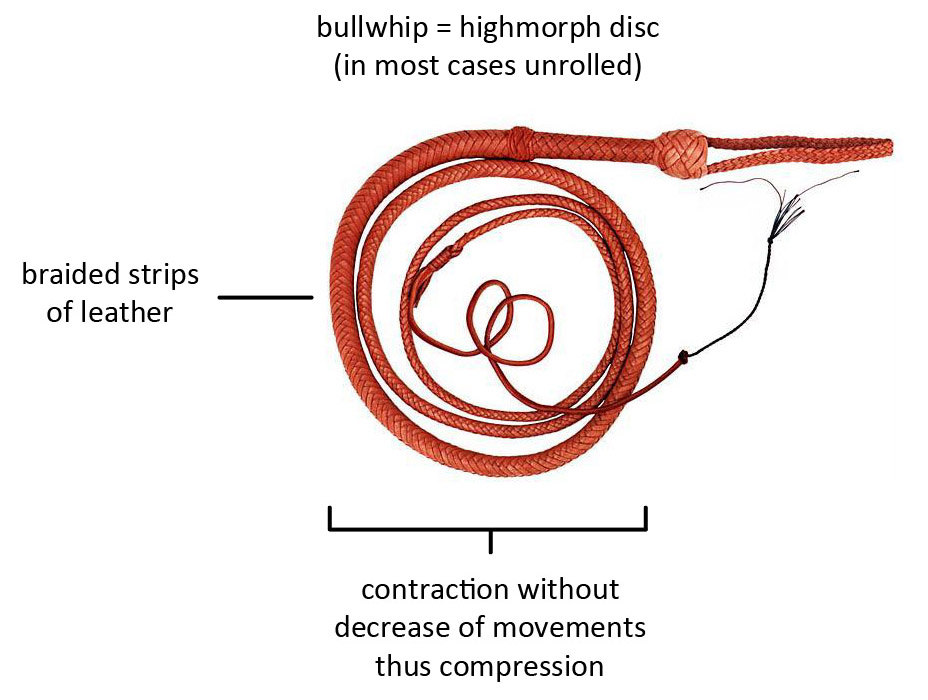
Image by Edward Lund, under CC BY 2.0 license. Image
was rotated 90° CCW, text and lines were added
But while the force is contractive, the number of movements do not decrease, thus dimensionality does not decrease. There are two reasons for this. First, the braided strips of leather do not fuse. The number of strips at the start of the whip is the same as the number of strips at the end of the whip. The strips only get thinner. And secondly, a whip that is thrown can form many different shapes as it can be thrown in many different ways but it never forms a spiral. The vortex thus makes a wrong move, and thus a compressive force builds up in the vortex.
If the whip was an unmorphed disc, it would not be able to produce a sonic boom either, because an unmorphed disc does not have braids. An unmorphed disc only consist of one single movement. The whip is a morphology between a disc and a swirl. It is the swirl that consists of a minimum of three movements, which are braided.
The image below show the movements of the swirl. There is a minimum of one core movement and two peripheral movements. The two peripheral movements are the minimum value, the vortex can also exist with more peripheral movements, thus more movements (meridians) in one braid. In the case of a vortex in fluids, solids or gas, we only see the sum movement. But it are examples like these that prove the existence of these individual movements.
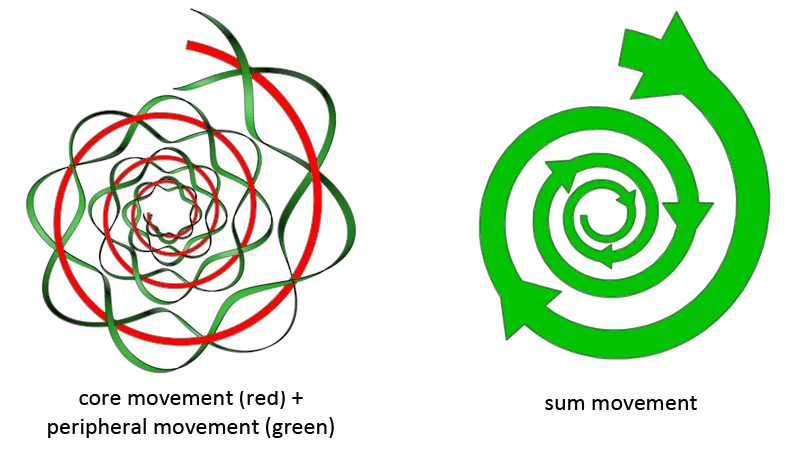
It is not only the swirl, but most vortices that have a periphery are assumed to contain these braided movements. It is quite possible that all vortices that are able to push and pull physical matter contain these braided patterns in their movements. A vortex that only has a core movement can not push or pull physical matter, and core movements alone are never braided. Again, it is only the sum movement that we are able to see with our eyes.
The current scientific explanation that a bullwhip makes a sonic boom because the tip exceeds the speed of sound can not be completely correct. It could be that the tip exceeds the speed of sound, but the braided strips of leather, which you see in every bullwhip, no matter if they're made of leather or nylon, is vital for the bullwhip to function. The vortex movement of a bullwhip is something that has never been understood until now. Anyone can imagine that this can be tested with a very simple experiment, which me or someone else definitely will conduct in the near future.
THE EXPLANATION THAT A BULLWHIP MAKES A SONIC BOOM BECAUSE THE TIP EXCEEDS THE SPEED OF SOUND IS INCOMPLETE. A BULLWHIP HAS TO BE BRAIDED OR ELSE IT CAN NOT PRODUCE A SONIC BOOM.
Like lightning is caused by a sudden release of tension, so is a sonic boom caused by a sudden release of compression. A sonic boom is thus the exact opposite of lightning. Because the sudden release of tension occurs over the negative dimensions, so must the sudden release of compression also occur over the negative dimensions. The end of the bullwhip thus must spawn a negative dimensional vortex. Because the disc is low dimensional, so must this mystery vortex also be low dimensional. The problem is that we cannot see this vortex. I do not know if anyone ever researched this or tried to capture images of this tiny sonic boom. But there is another way to see how a sonic boom looks like.
Image by Realbigtaco (Wikimedia), under CC BY-SA 3.0 license
Above there's an image of an american fighter jet going through the sound barrier. This produces a sonic boom and a vapor cone. The white vapor cone is clearly visible and it is clear to see that this vortex is a steep cone. This vortex makes a very expansive movement. The reason for this is that the airplane makes a movement in a straight line. And a single movement in a straight line is the movement that the spire makes. The spire is the lowest positive dimensional vortex in the sequence, thus close to the zero point. The faster the airplane moves, the closer the movement gets to the zero point. By increasing the speed the spire contracts, but the number of movements does not decrease to zero, it always stays one, because the movement persists as the movement of the spire, a movement in a straight line. Thus tension builds up in the vortex. When this tension reaches a maximum, the sudden release takes place and dimensionality falls back to the equilibrium.
Because the movement before the fallback was nearing close to the zero point, thus very low dimensional, the fallback is very far. From somewhere around 0.25D all the way up to 3.0D. That is why this vortex is so steep. It makes one highly expansive movement that spans 5 dimension levels. Airplanes never hit the zero point. I do not think it is possible to hit the zero point by moving an object at tremendous speeds (to be more accurate: at tremendous acceleration), otherwise it would be possible to produce a light flash by exceeding a certain speed limit. But that has never been observed. Now we know enough information to formulate a definition for a sonic boom.
SONIC BOOM = SUDDEN RELEASE OF COMPRESSION FROM WITHIN A VORTEX IN AIR WITH AN ABUNDANT NUMBER OF MERIDIANS. THIS RELEASE ENDS IN A FALLBACK TO THE EQUILIBRIUM IN A DIFFERENT CYCLE.
The braided strips of a bullwhip was the first hint that gave me the suggestion that the individual movements of a vortex, the meridians, are braided. Until then I thought that the right and left turning movements of a vortex intersected each other, this was what I concluded after looking at the double helical patterns on the trunk of trees. But this moving through one another of the individual movements is less logical to be physically possible. The braided movement is a more logical scenario. The discovery of the relation between this bullwhip and vortex movement opened a whole new perspective for me. From here on many things about the movement of vortices made more sense.
Snapping of a Towel
It is said that a wet towel can also be swung in a way that it produces a sonic boom. This is not without logic, for two reasons. First is that a towel is woven, it contains a zigzag pattern in the way that the fabric has been put together. Second is the water, which is required to make the louder snapping sound. Water is the state of equilibrium for the swirl, and the swirl is a vortex which has meridians that are braided, and is close to the same vortex which the whip creates with its movement. The whip is a highmorph disc, which is almost a lowmorph swirl (swirl and disc are subsequent spirals). A wet towels which is swung with force creates a movement which is equal to the movement of a swirl. Thus despite that a towel does not look like a braided spiral vortex, it still behaves like a braided spiral vortex, because of the properties of water. Thus the state of equilibrium of matter can create the same effect as an object that is weaved in the shape of that same vortex.
But a swirl is higher dimensional than a disc, thus the effect is less strong than that of a whip. The movement is less closer to the zero point, thus the fallback to the equilibrium is less strong. The speed of the tip of the towel less than the speed of a whip, but a supersonic snapping of a towel is possible, which is what is confirmed in the video below.
Still, the swirl is not an unmorphed swirl, instead it is a lowmorph swirl because it is absorbed into the towel, and the towel is lower dimensional than water. This example shows what effect the state of equilibrium for a particular substance can have on the behavior of other objects or substances when the two are mixed together (here one is absorbed by the other).
Tension and compression of sound
There is a separate page about sound that discusses several different aspects of sound waves. Three of these aspects of sound however will be discussed on this page. That is because those three things are about tension and compression. One of them is wineglass resonance, the second is the trumpeting of an elephant and whistling of a tea kettle (both have the same explanation), and the third is sound echo. One thing you need to know here but which has not been discussed yet is that audible sound comes from vortex movement of a amplicone, bulb or pylon in air. The exact location where sound is most audible for human beings lies somewhere around the position of those three vortices in the transformation sequence. This will be discussed on the page about sound.
Example #5 - Wineglass Resonance
You probably know that it is possible to make music with wineglasses. If you have a wineglass that is half full and you slide your finger or the palm of your hand over the edge of the glass the glass will make a singing sound. This sound is caused by resonance inside the glass. Take a look at the Youtube video below. The man in the video is Jamey Turner and he is very skillful at playing wineglass music. Quite entertaining to see him perform his art.
The key question here is: why does this only work with a wineglass? It does not work with a beer glass or any ordinary glass. Somehow the shape of the glass is crucial for it to be able to produce sound resonance. When we carefully examine the shape of a wineglass we can see that the lower part of the glass, called the stem and the foot, is a pylon with an unrolled revolute. The upper part of the glass, called the bowl, is a bulb.
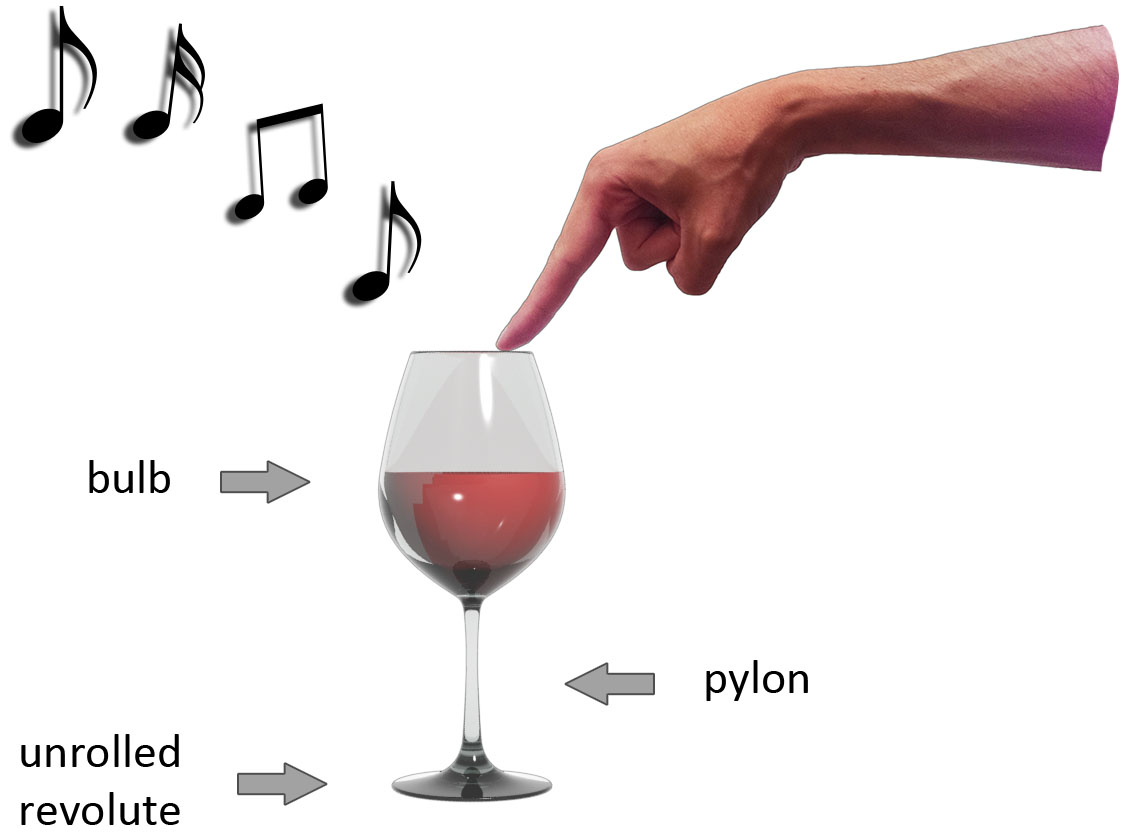
This example hardly needs any more commenting. By now you already understand what's happening. The only thing I need to add is that water needs to be added to the bowl because the bulb is not a hollow vortex. Wineglass resonance does not work when the glass is empty. By adding more or less water you can control the tone of the sound.
Example #6 - Trumpeting Elephant and Whistling Tea Kettle
The sound of a trumpeting elephant and the sound of a whistling tea kettle are both caused by the same phenomenon. The trunk of an elephant and the spout of a tea kettle both form a swirl. This is because the tube of air that runs through it is shaped like a cone. But the shape of both of these tubes does not form a spiral.
In the example on the photos you can see that only the first part of the swirl goes in the right direction, but then it makes a wrong turn and starts to bend in the exact opposite direction than it should. Because the tube is still getting narrower and narrower, a compressive force builds up due to the number of meridians still being equal in number. When the air exits the nozzle a release of this force takes place. This is not like the release of compression with a sonic boom, because here the maximum compression was not reached. No inversion to the negative dimensions took place, but still a strong release of tension where the movement again falls back to the equilibrium.
|
|
|
A tea kettle makes a whistling sound because of the same reason, release of compression. If you look at how a traditional tea kettle looks like then you should notice that the shape of the spout is very similar to the pose of an elephant's trunk when trumpeting. But the primary reason for this shape is a functional one. The spout first bends upwards because you don't want to spill any hot water. Then it bends downward at the tip so that its easier to pour the water. I am very sure that the first people who designed this type of tea kettle were unaware that this shape would also produce a better whistle. But it does, pure by coincidence. If the spout is straight then the kettle should also whistle, because that too is a wrong move, but the whistle should be less strong. By first bending in the right direction and then bending in the opposite you should get the best whistle. The elephant knows that, and now we know that too.
Example #7 - Echo
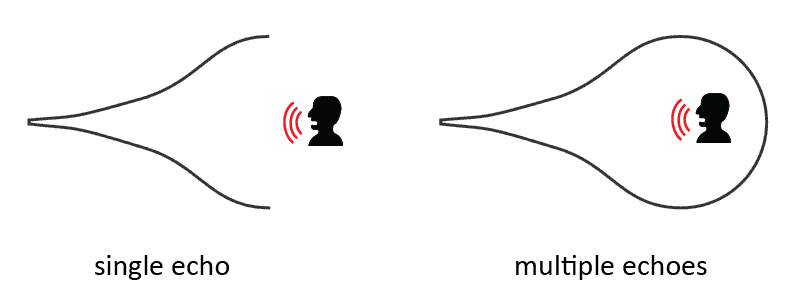
Another phenomenon that is caused by tension and compression is sound echo. The current scientific explanation for echo is that it can be explained as a wave that has been reflected by a discontinuity in the propagation medium, and returns with sufficient magnitude and delay to be perceived. In other words, the sound is reflected of walls and hard surfaces and then bounces back to you. But if you think further than that then you are able to conclude that this explanation has to be incomplete.

If you stand in front of a wall, or any kind of wall or hard surface, and you yell out loud, then there is no echo. It does not matter how big the wall is or how far you are standing from the wall or at what angle you face the wall, echo only happens in very few specific locations. If reflection of a wall was the only explanation, then you would get a lot of echo from just standing and yelling inside a large chamber. No one has been able to explain why these very specific locations produce echo. That is, until now...
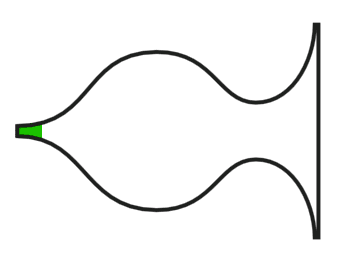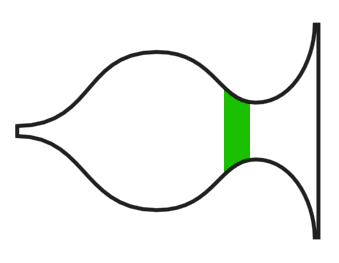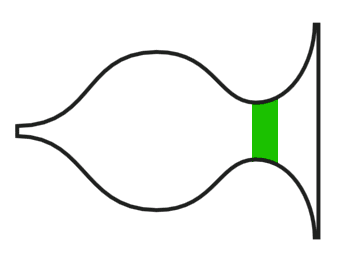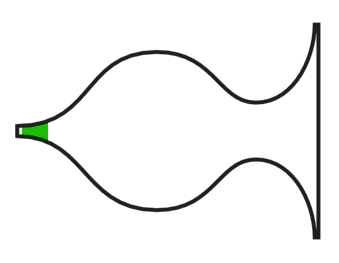
Sound that comes back to you does so because of the shape of the environment. The shape of the environment shows a resemblance with the shape of that of a bulb with an unrolled revolute, unrolled swirl, or both. What you get is the same kind of back and forth vortex movement that happens inside a Helmholtz resonator, except here the person who makes the sound, thus the sound source, is located inside the resonator instead of outside. There are different versions of echo. The vortex movement can start as a bulb, move to a pylon, and then bounce back after having progressed a while as an unrolled revolute, or it can go the other direction and bounce back after progressing as an unrolled swirl. In a closed environment the vortex can oscillate multiple times, therefore spawning multiple echoes.
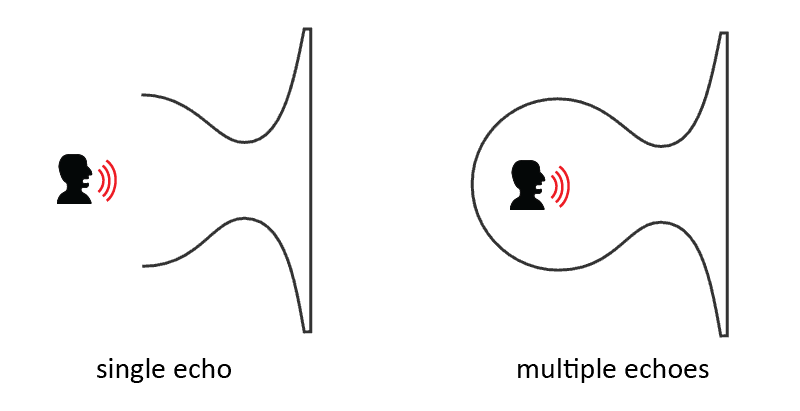
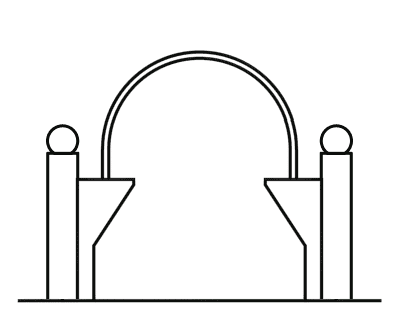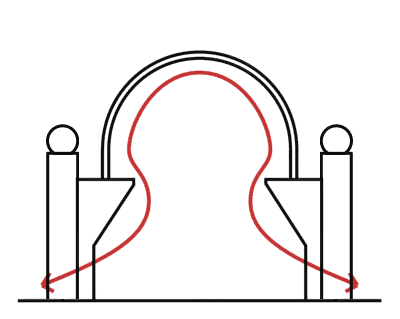
The image above shows the shape of the environment for an echo that is formed by an unrolled revolute. This type of echo is what I call a 'tension echo'. That this type of echo is called a tension echo does not mean that there is no compression. Only in the single echo there is only tension. In a closed environment, the first half of the bulb lies below the equilibrium thus here some compression takes place.
If you look for examples of this kind of echo in our environment, then they are not hard to find. It sometimes takes a little bit of puzzling to figure out what shape it is that drives an echo. The Gol Gumbaz in Bijapur, India is an example of a tension echo location.
Gol Gumbaz in Bijapur, India
Gol Gumbaz is the mausoleum of Mohammed Adil Shah (1627-55) of the Adil Shahi dynasty of Indian sultans, who ruled the Sultanate of Bijapur from 1490 to 1686. The tomb, located in the city of Bijapur, or Vijapur in Karnataka, southern India, was built in 1659 by the famous architect, Yaqut of Dabul. The structure consists of a massive square chamber measuring nearly 50 m (160 ft) on each side and covered by a huge dome 43.3 m (142 ft) in diameter making it among one of the largest dome structures in world. The acoustics of the enclosed place make it a whispering gallery where even the smallest sound is heard across the other side of the Gumbaz. At the periphery of the dome is a circular balcony where visitors can witness the astounding whispering gallery. Any whisper, clap or sound gets echoed around 7 times. Anything whispered from one corner of the gallery can be heard clearly on the diagonally opposite side. It is also said that the Sultan, Ibrahim Adil Shah and his Queen used to converse in the same manner. During his time, the musicians used to sing, seated in the whispering gallery so that the sound produced could reach every corner of the hall [text from Wikipedia].
Take a look at the video above. And then take a good look at how the environment looks like, the shape of the dome, the balcony and the chamber below. The dome is the bulb. The balcony forms the narrow neck towards the revolute and the chamber below forms the unrolled revolute. If the balcony wasn't there, then the echo would not be there either. There are open doors and doors with smaller openings in the chamber below. If those doors and openings would all the closed then the effect would be a less or none because the unrolled revolute would be shorter.
_UnderCCBYSA3.0.jpg) Image by Mukul Banerjee (Wikimedia), under CC BY-SA 3.0 license |
 |
One thing I have to make very clear is that it is not the vortex that we humans hear. Human beings can not hear vortices. What we hear are the waves that are connected to and emitted from these vortices. And these waves become most audible when they are emitted from a position somewhere close to the central balance point.
Torre Bianca in Bellinzona, Switzerland
Castelgrande is a fortification that lies in Bellinzona, Switzerland. The stronghold includes a complex of buildings which were part of the old keep in the castle. In the center of the keep is the tallest tower of the Castelgrande, the Torre Bianca or White Tower, which dates from the 13th century. In the bottom chamber of this tower is an echo spot. The tower itself has a hollow shaft running from the top of the tower all the way down to the bottom chamber.
The fact that this chamber has an echo makes it a nice tourist attraction. Again, what you need to do is take a good look at the Youtube video and see how the environment looks like, the shape of chamber. You need to think back at what was said at the start of this page to be able to solve this one. Because this one is a bit different then the previous example.
_UnderCCBYSA3.0.JPG) Image by Jungpionier (Wikimedia), under CC BY-SA 3.0 license |
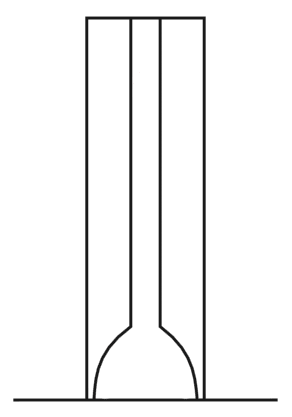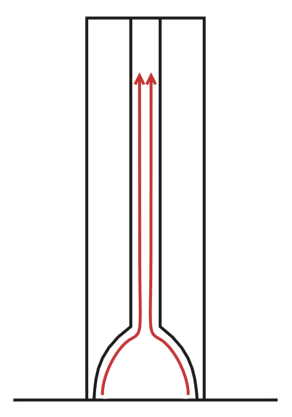 |
This echo is, like the previous example, a tension echo. Except here the revolute is unrolled at the start of the revolute instead of after making a 90 degree turn as with the previous example. This makes the tension weaker, and a longer unrolling is needed before the tension is strong enough for the vortex movement to come to a standstill and bounce back. This kind of echo would not work if the shaft was a lot shorter.
Echo in a Valley
If an echo can be caused by an unrolled revolute, like in the previous two examples, then it is likely that an echo can also be caused by an unrolled swirl.
Above is an image that shows the shape of the environment for an echo that is formed by an unrolled swirl. This type of echo is what I call a 'compression echo'. That this type of echo is called a compression echo does not mean that there is no tension. Only in the single echo there is only compression. In a closed environment, the second half of the bulb lies above the equilibrium thus here some tension takes place. If you look for examples of this kind of echo in our environment, then you too will find them. Take a look at the two videos below.
First video is of an echo point in Matheran, a city in the Indian state of Maharashtra. Again, you need to take a good look at the surroundings. One thing you will notice by looking at this and other similar echo points in valleys, is that there are steep walls at the top of these valleys. This is the main reason that people believe that the sound comes back to you because it reflects of these walls. But if you understand vortex movement, and if you know what an oscillation bulb is, then you understand that there is a different reason why these cliffs are essential for the echo.
The second video, filmed in Utah, United States, shows the same principles in the environment. Same two steep cliffs at both ends, with less steep slopes of the mountain sides in between the vertical cliffs (you need to turn up the volume to hear the echo of the flute). A third example can be found here.
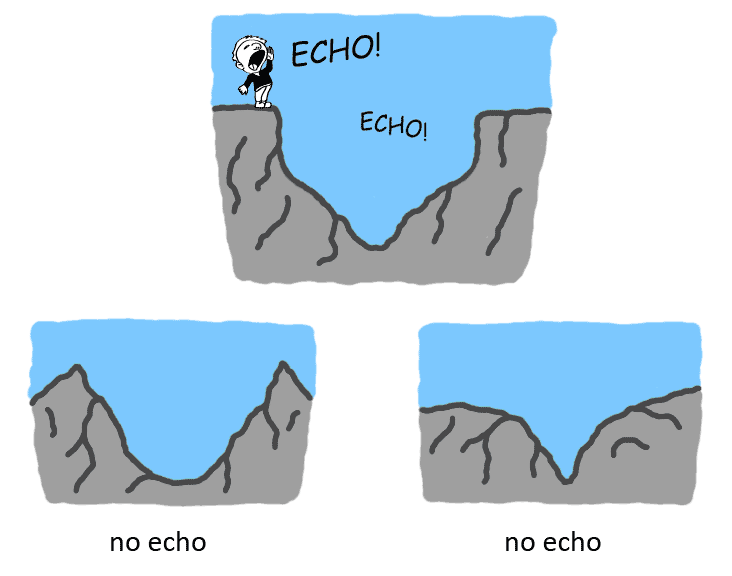
The reason that the valley produces an echo is because the shape of the valley is that of a bulb with an unrolled swirl at the bottom. Only valleys whose shape come close to this produce an echo, most valleys do not produce an echo because it needs steep cliffs at either side with a conical base underneath.
THE NOTION THAT SOUND ECHOES IN A VALLEY BECAUSE THE SOUND WAVES BOUNCE OF A STEEP CLIFF IS INCORRECT. THE STEEPNESS IS NEEDED BECAUSE IT FORMS THE BOTTOM HALF OF THE BULB, BUT THE SOUND ECHOES BECAUSE THE VORTEX MOVES TO THE BOTTOM OF THE VALLEY AND THEN UP AGAIN, GOING FROM BULB TO UNROLLED SWIRL BACK TO BULB AGAIN.
The shape of the bulb and unrolled swirl is not the normal shape, but the dedimensionalized vortex shape (see page titled 'More About Vortices'). The shape is only defined along two axes and stretched out along the third axis. But the normal vortex shapes should also work as sound echo locations.
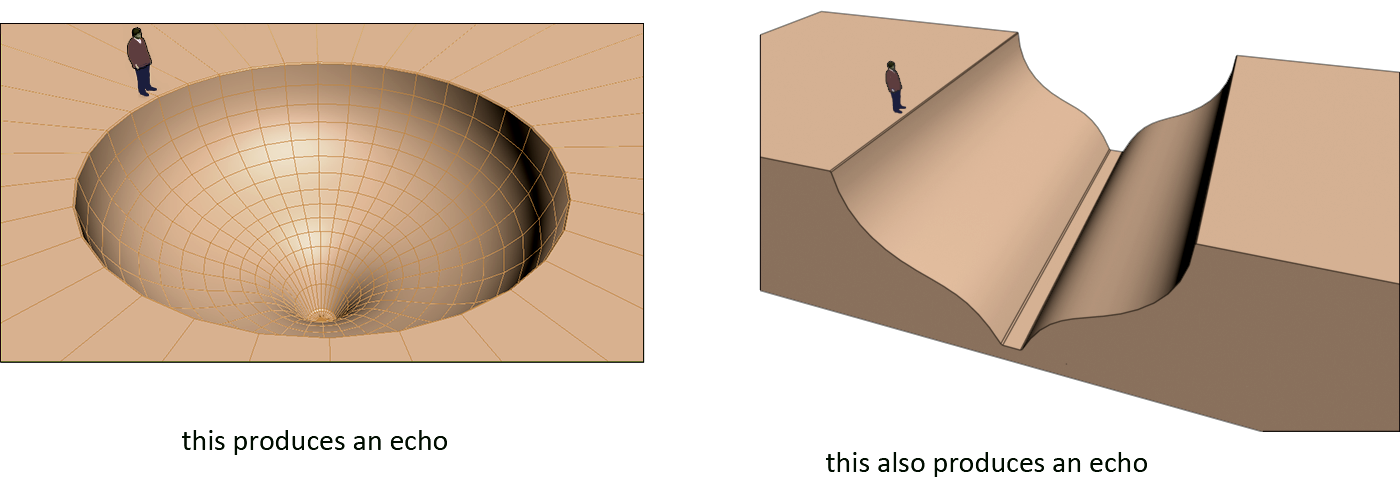
But again I need to state very clearly that we do not hear the vortices. What we hear are the sound waves that are connected to these vortices. If the above is all correct, then a valley should always produce only a single echo. The problem is that I haven't been able to confirm whether this is true. If anyone of you has ever been to such an echo point, and can confirm whether there is only one or multiple echoes, then please e-mail me.
None of the above examples produced an ideal echo, because none of these examples formed a full oscillation bulb. So in none of these examples, both the tension and the compression were ideal. One of these two forces was always less strong than the other. Below shows a type of echo in which both buildup of tension and compression is strong.
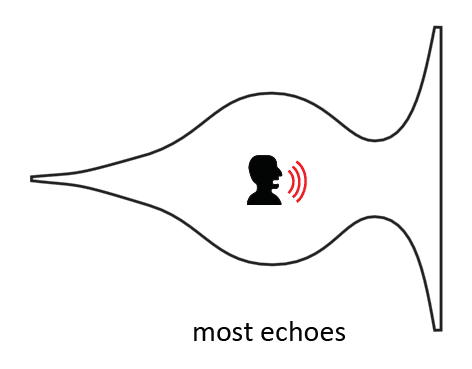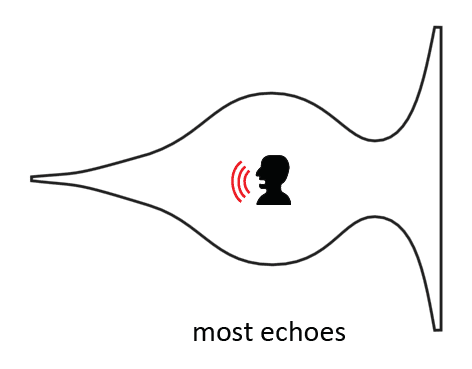
This type of echo is what I call a 'balanced echo'. I call it a balanced echo because the center of oscillation is the center of the bulb, thus the central balance point. All the examples of echo that we've seen are not exactly centered around the central balance point. I still haven't observed an echo like this in any example.
It would be quite interesting to test this kind of sound echo in a test chamber. If all that is on this page is correct, then this might produce a very good, repetitive echo. What I'm not exactly sure of is if the center of the bulb is also the center of the audible sound region of the transformation sequence. It could be that the center position of audible sound, thus the position where audible sound is best heard by humans, lies somewhat higher in the sequence, somewhere at the start of the pylon. Another thing that has to be considered is that the echo might not work if the chamber is completely sealed. There probably need to be some holes in the chamber otherwise the air cannot flow. A Helmholtz resonator has a hole on both sides, otherwise it does not work. The Gol Gumbaz also has open doors. This we will all find out in the near future by conducting some creative experiments. Now that we're into sound, lets continue this topic on the next page.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |




_UnderCCBYSA3.0.JPG)

_Edited_UnderCCBY2.0.jpg)