Temperature

Action and Reaction

Sir Isaac Newtons third law of motion states that for every action (force) there is an equal and opposite reaction. In other words, if object A exerts a force on object B, then object B also exerts an equal and opposite force on object A. A similar opposite reaction also takes place on one scale level when a change occurs in dimensionality on another scale level. The difference here with Newton's law is that not objects are exerting a force on each other by collision, but the forces act on vortices that are located within other vortices, as residential matter. It is almost like a vortex exerts a force onto itself, because the much smaller vortices that give the counter reaction to this force are located within that larger vortex that exerts the force.

To give you an idea of this, we now take a look at temperature. When we carefully observe vortex movement within the mesocyclic level, then we often see an increase in dimensionality go side by side with a increase in temperature, and a decrease in dimensionality go side by side with a decrease in temperature.
 

Image by U.S.Federal Government

Photo courtesy of National Nuclear Security Administration / Nevada Site Office

One such example is a mushroom cloud of a large explosion. The hottest part of the mushroom cloud is the center ring inside the mushroom head. This center ring is the gyroduct, which is higher dimensional than the stem of the mushroom (pilaster) or the head of the mushroom (revolute).

Another example is the jet engine, where movement of the air is first split into many smaller movements (both still in the mesocyclic level). Splitting increases dimensionality, because it (temporarily) increases the number of meridians. Increase of meridians is one method of increasing dimensionality (without increasing the dimensionality level). The air also increases in dimensionality because the air makes an expansive movement, in which the flow movement becomes hollow. This increase in dimensionality on a mesocyclic scale increases the temperature, thus decreases dimensionality on a microcyclic scale.

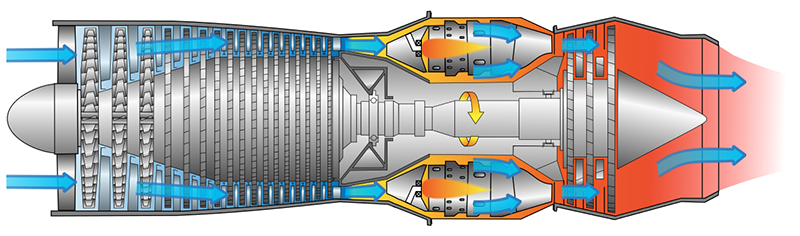
Image by Jeff Dahl (Wikimedia), under CC BY-SA 3.0 license. Image was edited by removal of text.

The increase in temperature is a result of what happens in the microcyclic scale level. We know that particles move faster when heat is increased, and move slower when cooled down. And we also know by now that faster movement means lower dimensionality. So here, it appears that the opposite has happened as to what took place on a larger, mesocyclic level. This decrease in dimensionality in the microcyclic level is the opposite of the increase of dimensionality in the mesocyclic scale level.

This only explains the rise in temperature. It does not explain any of the other mechanisms of a jet engine, most important its thrust power. The thrusting power is the result of the split movements merging again at the exhaust of the jet engine. But what exactly causes the strong force is not yet clear to me.

We have found an effect that is a variation of Newtons law. The explanation of this effect correlates with the explanations we have for effects that can be explained with Newton's law. The tricky part was that the reaction happened in the microcyclic level, thus on a different scale level, and the objects, here vortices, touch by existing as residential matter within the larger vortex.

TEMPERATURE = DIMENSIONALITY ON MICROCYCLIC SCALE

But is this linking of observed phenomena with action and reaction enough to conclude that temperature is linked to microscopic or even smaller contraction and expansion? Is the above definition correct? Lets try the more obvious approach and take a look deep into the microcyclic scale level with the tools that are available today.

Atomic Orbitals

Atomic orbitals are cloud like structures around the nucleus of an atom that contain the atoms electrons. These orbitals have electrons containing different amounts of energy, and it is possible for electrons to jump to and from different orbitals. When this happens energy either needs to be added or released. The number of orbitals present in an atom is completely dependent on the number of electrons present in the atom. Specifically, atomic orbitals are the possible quantum states of an individual electron in the collection of electrons around a single atom, as described by the orbital function.

These shapes are among the smallest that we humans today have been able to determine (but we are not able to see them with a microscope). These atomic orbitals are relevant for what is discussed on this page because I believe that they are different vortices in a sequence, and for this I have several reasons.

Image by ProkopHapala (Wikimedia). Background and foreground color
was altered, image rotated 90 degrees CCW and text removed.

The first clue comes from the shapes of these atomic orbitals. These look like strongly defined geometric shapes. Like shapes that can be described by mathematics, thus by an equation. As a matter of fact, these atomic orbitals already have been described by mathematics. They are described by the Schrödinger equation. All vortices are strongly defined geometric shapes. If you look at the basic shape of the vortices that have been identified and classified until now, then you can sense that it is very likely that for those vortices too it should be possible to describe their shape with mathematics. There should be an equation for the whole transformation sequence. Although it is not known today, there is one clue that suggests that imaginary numbers are needed to formulate such an equation. Reason for this is the Hopf fibration, which could be an equation that is close to being the correct equation to describe the direction of the meridians for a revolute vortex. The Hopf fibration requires imaginary numbers. The Schrödinger equation also requires imaginary numbers.
 

The next clue comes from looking at what atoms are made of. Atoms consist of a central nucleus (protons and neutrons) surrounded by a cloud of electrons. For many years, scientists imagined electrons as points orbiting around a nucleus, just like planets that rotate around a sun. This theory has been proven wrong by quantum theory more than 60 years ago. When we look at the images of atomic orbitals we do not see little dots around a nucleus. But many scientists are still holding on to this 'point' theory, so now the electrons are described as electron clouds where the shape of the cloud is explained as a probability of finding any electron of an atom in any specific region around the atom's nucleus. A cloud around a central core, that does sound a bit like the periphery of a vortex that moves around the core of a vortex, with the difference here that the core is not a trajectory but a single point.
 

Third clue is that there are no atoms in a vacuum. Or to be more accurate, there are only very few atoms inside a high vacuum. (An ideal vacuum, which only exists in theory, would contain no atoms). But the peculiar thing is that a vacuum can be achieved by expanding a sealed volume of air, like when pulling on a plunger of a syringe which outer end has been sealed. If there are atoms in air, but no atoms in that same air which has been transformed to a vacuum, then where did the atoms go? A likely explanation is that the atoms are vortices that morphed from one type to another the moment the volume expanded, which happened as a counter-reaction to what occurred on the mesocyclic scale. A high vacuum is a state of the third cycle (fifth half-cycle), which is achieved by dilation of air, dilation of the bulb and other vortices. It could very well be that the disappearing of the atoms is due to dedilation, the reverse process of dilation, that takes place on the microcyclic scale the moment the air expands. Because of the dedilation, and the transformation of the microcyclic vortices into smaller, lower dimensional vortex types, the atoms become undetectable. Or it could be that what replaces the air molecules is something that is already detectable with today's technology, but that we have failed to comprehend what these transformed molecules are. A different vortex type could indicate a whole different phenomenon.

If temperature is dimensionality on microcyclic scale, and if it is so that these different quantum states of atoms are different vortices in a sequence, then a change in temperature should result in change of quantum state. So do these different energy levels relate to temperature? The following text is from Wikipedia.

Higher temperature causes fluid atoms and molecules to move faster increasing their translational energy and can thermally excite (non-radiatively) polyatomic molecules to a higher average distribution of vibrational and rotational energy levels. This means as temperature rises, translational, vibrational, and rotational contributions to molecular heat capacity let molecules absorb heat and hold more internal energy. Conduction of heat typically occurs as molecules or atoms collide transferring the heat between each other. At even higher temperatures, electrons can be thermally excited to higher energy orbitals in atoms or molecules.

So these energy levels, thus different shapes of atomic orbitals are influenced by temperature. Most of us are aware that higher temperature means more energy. So perhaps you already felt this one coming. With this we are now able to formulate yet another simple definition:
 

ATOM = VERY SMALL VORTEX

Not much more than this is certain at this point. It could be that the electron cloud is the periphery of a vortex and the nucleus is the core of a vortex. Many of the subatomic particles we know today, quarks, neutrinos, muons,  photons, bosons, etc, could be very small vortices. Either they are very small vortices or they are clusters of very small vortices or they are components of very small vortices. Some of the behavior of these tiny particles that exist in the microccyclic scale level can be understood by understanding cause and effect brought on by changes that happen in the mesocyclic level. One of these effects we now have been able to unravel.
 

A CHANGE IN DIMENSIONALITY ON THE MESOCYCLIC SCALE RESULTS IN AN OPPOSITE CHANGE IN DIMENSIONALITY ON THE MICROCYCLIC SCALE. A CHANGE IN DIMENSIONALITY ON THE MICROCYCLIC SCALE RESULTS IN AN OPPOSITE CHANGE IN DIMENSIONALITY ON THE MESOCYCLIC SCALE. INCREASE AS A REACTION TO DECREASE AND DECREASE AS A REACTION TO INCREASE.

And this change in dimensionality can happen in more than one way. One way it can happen is by an increase or decrease of temperature, which is an indication that the non-visible vortices in the microcosm expand or contract.

You also need to be aware that the movement of a single vortex in one scale level does not influence the movement in the higher scale level (well, it probably does actually, but the effect then must be very very small). The presence of a single vortex on the mesocyclic scale does not influence dimensionality on the macrocyclic scale. But this vortex does influence the dimensionality on the microcyclic scale. You need a lot of mesocyclic vortices to influence the macrocyclic scale level. I will now show you a series of examples that show how the mesocyclic scale level influences the microcyclic scale level, and vice versa. Remember that you can click on the orange yin yang symbol at the top right corner of this page to view the table of properties of high and low dimensionality.

Example #1 - The States of Matter

Think about water in the form of a chunk of ice. Ice is cold and a cold temperature reveals that dimensionality on the microcyclic scale is high (yin). Ice is also hard and crystallized, indicating that its dimensionality on mesocyclic scale is low (yang). When we heat up ice, it will melt and become liquid. On mesocyclic scale, liquid water is higher dimensional than ice. We know that because water has more freedom of movement than ice. The water has become higher dimensional on the mesocyclic scale by increasing the temperature, thus by reducing dimensionality on the microcyclic scale.

If we heat water up further it will evaporate. Water vapor is higher dimensional than liquid water. Water vapor has more freedom of movement than liquid water. The water has thus become higher dimensional on the mesocyclic scale, while the higher temperature reveals that dimensionality on the microcyclic scale has been reduced. The higher the dimensionality on the mesocyclic scale, the lower the dimensionality on the microcyclic scale.

These states of matter have strong defined transition temperatures. In between these rapid transitions a substance appears to stay the same, but although it is less evident, dimensionality still changes in between these transition temperatures. The next three examples show a change in dimensionality within the same state of matter. The first in a gaseous substance, then in a liquid, and lastly in a solid.

Example #2 – Hot Air Balloon

One property of matter that is affected by a change in dimensionality is weight. Higher dimensional gives less weight, lower dimensional gives more weight. When temperature increases, thus when dimensionality on the microcyclic scale decreases, dimensionality on the mesocyclic scale increases, thus air becomes lighter. The hot air inside the balloon is therefore lighter than the air around it, that is why the balloon can rise up.

This can also be explained by only considering the air density. The air becomes lighter because it expands, it increases in volume. Therefore the weight of the air is less for the same amount of volume as it was before the air was heated. The following example takes another look at air density.

Example #3 – Air Density

When temperature decreases, air density becomes higher. This is because the drop in temperature, thus an increase in dimensionality on the microcyclic scale results in a decrease in dimensionality on the mesocyclic scale. A consequence of this is that wind gets a better grip on sails. Lower dimensional means more friction / less penetrable. When temperature increases, thus when dimensionality on the microcyclic scale decreases, air density becomes lower due to the increase of dimensionality on a the mesocyclic scale. Below is a Youtube video of a kiteboarder named Alex Aguera explaining how air temperature is a critical factor in considering the power of wind.

Example #4 – Convection

Convection is the flow of heat as a mesocyclic movement of matter from a region with a higher temperature to a region with a lower temperature. Boiling water by heating up the water above a heat source is one example of heat transfer by convection. The water at the bottom of the pan gets hot first while the water at the top is still cool. The hot water rises to the top forcing the cooler, more dense water down where it gets heated. This creates a convection current, in which the flow of the water follow a continues circular motion.

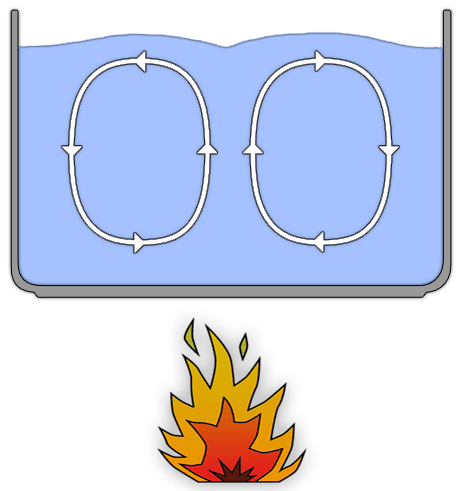
The water does not need to be heated up all the way to boiling temperatures for convection to take place. Convection also occurs at much lower temperatures, as long as there is a heat difference between different regions within the same fluid. The following example shows convection in a heated volume of water, below cooking temperature.

Convection is the movement of the revodome. This high dimensional vortex movement is induced because of the rise in temperature of the fluid. The fluid becomes lower dimensional on the microcyclic scale and thereby reacts by becoming higher dimensional on a mesocyclic scale. The very small non-visible movements of the water (at atomic scale) contract and at the same time the much larger visible movement of the water expands. When water at room temperature is at rest its dimensionality is equal to that of the swirl, because the swirl is the state of equilibrium for water. Due to the increase in dimensionality the water starts to move as a revodome, which is a vortex located in the third half-cycle, as opposed to the first half-cycle where the swirl is located.

Example #5 – Viscosity

Here is another video that shows how dimensionality on the mesocyclic scale of a fluid is affected by temperature. It's a science fair project that involves dropping a marble into a container of honey at three different temperatures and timing how long it takes to hit the bottom. Nine marble drops each at 50, 70 and 100 degrees Fahrenheit. The length of time is used as a proxy to determine how temperature affects the viscosity of honey.

Viscosity is a measure of the resistance of a fluid against being deformed. Low viscosity means that the fluid is thin, high viscosity means that the fluid is thick. When temperature increases, thus dimensionality on the microcyclic scale decreases, then dimensionality on the mesocyclic scale increases, thus the viscosity of the fluid decreases. Therefore, the honey becomes thinner.

Example #6 – Solid Metals

Image by Jeff Kubina, under CC BY-SA 2.0 license

Most metals can not be molded at room temperature. Metals need to be heated up to a higher temperature before it can be forged with a hammer. By increasing temperature, thus decreasing dimensionality on the microcyclic scale, we thereby increase dimensionality on mesocyclic scale. Higher dimensional on mesocyclic scale means that the metal becomes softer, loose, less constricted.

Not all materials become more flexible when heated to higher temperatures. Some materials harden when heated up, with an additional difference that the change in flexibility is not a temporary change but a permanent one. An examples of this is clay. I'm not sure why these materials react the opposite way. It could be that the hardening is a reaction to when a movement crosses an EM crossing location, like the crossing of the zero point when an object combusts.

Color

Color is another phenomenon that provides us with information about the state of vortices at the microcyclic level. It is a visual aid provided for us humans for allowing us to see information about the shapes that are too small for us to see. Some of this was explained on the page about the color spectrum.

Conclusion

On this page, we end with the knowledge that particles are very small vortices. But what implications does this have? We know that vortices are visible elements of a larger non-visible element. A vortex is the only part of a wave within the onefield that intersects our physical world. We only see the vortex, but there are spherical in and outgoing waves connected to these vortices that we can not see with our eyes. We can not see the start or end of what is connected to that vortex. So if particles are vortices, then that means that particles appear to be discrete objects in our physical world, but in our physical plus the non-physical world put together these are not discrete objects. Everything is connected, so are these subatomic particles. Particles are just a small parts of larger waves in the onefield. Still not that much has been said about these waves within the onefield. The first page that will explain many different things about these waves is the page about sound. Before that we will discuss tension and compression, coming on the next page.

THERE ARE NO DISCRETE PARTICLES IN THE UNIVERSE