The Bells
Bells are hollow vortices within the third half-cycle. When a spiral with one arm in the first half-cycle dilates, it becomes a disk. When a spiral with two arms dilates, it becomes a bell. The movement of a bell does not appear to go inward nor outward. Its movement appears to be looping at the same continuous dimensionality level. Bells are stand-alone vortices that do not appear to connect directly to any other vortex. I'm not 100% sure about this, but I think that a bell takes in the position of the same dimensionality level of the low end of the spiral from which it dilates. But it is located one cycle higher in the sequence than the spirals from the first half-cycle.
A bell looks very much the same on the outside as the spiral from which it dilated from. The shape of the bell is the same as that of a spiral whose movement has relocated itself to the outer edge of the vortex. The outer edge is still what is similar to the non-dilated form, yet the vortex has become hollow.
There are three known bell vortices so far: the vessel, the revodome and the tubular ring. There could be at least two more bells within the third half-cycle. One should be the dilation of the swirl with two arms, the other should be the dilation of the disc spiral with two arms. It could be that these vortices look closely similar to the disks that are the result of a dilation of a spiral with only one arm (which are belts in this case).
A bulb with the equivalent of two spiral arms can morph into a vessel.
A revolute with two spiral arms can dilate into a revodome.
A scroll ring with two spiral arms can dilate into a tubular ring.
These three bells also form a morph sequence. Every bell in the sequence can morph into the next higher dimensional bell within the same half-cycle.
Disks are states of equilibria for metals. It is not known if bells are states of equilibria for metals as well. It is more likely however that bells are the states of equilibria for low vacuums. The suprabells are the states of equilibria for high vacuums.
Bells are hollow, but it might be that at some situations they can co-exist with the spirals from the first half-cycle. The bells then might be an encapsulation of the spirals, a vortex in the form of an outer shell that encircles another vortex of a different class. This is theoretical, but there is one observation with a revolute vortex mentioned further below on this page which might suggest that that is a situation that can occur.
Vessel

| Classification | Third bell of the second cycle |
| Dimension | 2.75D |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | A vessel means either a ship or a hollow container, that is what its shape (including when cut in half) in both cases resembles |
When a bulb with the equivalent of two spiral arms dilates, it changes into a vessel. The shape of this vortex is identical to the bulb, a spiral from the first half-cycle, with the difference that this vortex is hollow on the inside, and the bulb is solid on the inside (although it might be that at some point this vortex is an encapsulation of a bulb spiral). This vortex is a thin shell that is ellipsoidal in shape, almost like the shell of an egg, only more symmetrical.
Other bells make a rotational movement, yet this bell does not. The vessel is a non-rotational vortex. The reason for that is the same reason as to why a bulb does not have visible spiral arms. The bulb is located on the central balance point, therefore the spiral arms do not rotate inward, nor outward, because its tendency to do either is in stasis. The vessel is also located on a central balance point, therefore the rotation of the hull is neither clockwise or anti-clockwise, it too is in stasis.
Three examples of vessels are: swirling flow in a cylinder (mesocyclic), some elliptical galaxies (macrocyclic) and anti-bubbles (mesocyclic).
Swirling Flow in a Cylindrical Container

Image by M.P.Escudier. Image was taken
from A Gallery of Fluid Motion by
Cambridge University.
The photo above shows both a revodome and a vessel. The vortex was produced by means of a flow in a closed cylindrical container completely full of a glycerine-water mixture by rotating one end-wall. The cut-though shape of the vortex was made visible by using laser-induced fluorescence. The vortex in the middle is a vessel. In this case the vessel is slightly upmorphed. We know this because this vessel has a thin central axis, which is a feature that only the revodome has. So we can conclude that its shape is a morphology between a vessel and a revodome.
Elliptical Galaxies (Bright Types)

Image by NASA, STScl and WikiSky
There are two types of elliptical galaxies. The first type we already discussed on the page about the ladders. Soft ellipticals are bulbs. But bright ellipticals are vessels. The reason why these vessel galaxies look so evenly dense on the outside is because they are hollow, thus all the movement is concentrated at the outer edge of the galaxy, there's either nothing or relatively little star formation inside the shell.

Bulbs however are not hollow, the movement is evenly divided over its entire volume that is why these bulb galaxies look most dense where they are the thickest. The bulb galaxies thus have a soft appearance. Here I call one of them soft ellipticals and the other bright ellipticals.
Anti-Bubbles
A common water bubble is a sphere of air surrounded by water. A soap bubble is a thin film of water mixed with soap that has both air on its inside and on its outside. An anti-bubble however is a thin layer of gas with a liquid on both the inside and the outside. Anti-bubbles are less common and you might never have seen them or might never have recognized them to be anti-bubbles.
An anti-bubble is an example of a vessel, thus a dilated bulb. Only the thin layer of gas is what embodies the vessel, the surrounding water around it is not part of the vortex. Some examples of anti-bubbles can be seen in the video above.
Revodome

| Classification | Fourth bell of the second cycle |
| Dimension | 3.75D |
| Positive / Negative | Positive |
| Core | Unknown |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name |
Revo because of its rotational movement, as in 'revolving' Dome because of its dome shape |
When a revolute with two spiral arms dilates, it changes into a revodome. The shape of this vortex is identical to the revolute, a spiral from the first half-cycle, with the difference that this vortex is hollow on the inside, and the revolute has spiral arms rotating inward (although it might be that at some point this vortex is an encapsulation of a revolute). The revodome is a rotational vortex.

If you cut a revolute in half, then you see two shapes in its cross-section that are somewhat, but not quite, circular. The same happens when you cut a revodome in half. What you see are two openings that are not quite circular, but both rather flattened at one side. Yet, when a revodome morphs into a tubular ring, its cross section becomes more and more circular until it is fully circular. This difference is illustrated in the image above.
Two examples of revodomes are: mushroom clouds with a dilated stem (mesocyclic) and again the swirling flow in a rotating cyclinder (mesocyclic).
Mushroom Clouds with a Dilated Stem
Revolutes and revodome look very much the same on the outside. Their shape is similar. When we look at a revolute vortex from a large explosion, which forms the head of the mushroom cloud, then we can in many cases not tell whether the mushroom head is a revolute or revodome. Only when the vortex is somewhat transparent, and we can to some extent see its internal structure, only then we know if the vortex has spiral arms spiraling inward, thus only then we know which of the two vortex types the vortex belongs to.
However, there are two indirect ways we can tell which vortex type is the correct vortex type. One is when a cradle forms underneath the mushroom cloud, which strongly suggests that the vortex above it is a revolute spiral. The other situation is when the pylon or the pilaster underneath the revolute is dilated. Dilation of a spiral is not easy to see, but dilation of any bridge or ladder is easy to see. The vortex expands into layers, taking the form of a white vapor cloud.

Most explosions do not form a pilaster or pylon in a dilated form, but some do. The photo above shows one such example. When the stem of the mushroom cloud is dilated, it means that the revolute vortex above it must be dilated as well. This is one way to identify a revodome in an observation.
Swirling Flow in a Cylindrical Container

Image by M.P.Escudier. Image was taken
from A Gallery of Fluid Motion by
Cambridge University.
This is the same photo that was shown in a previous example for the vessel vortex. The photo above shows both a revodome and a vessel. The vortex at the top is a revodome.
Tubular Ring

| Classification | Fifth bell of the second cycle |
| Dimension | 4.75D |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | Tubular because this vortex is tubular. Ring because it has the shape of a ring |
When a scroll ring with two spiral arms dilates, it changes into a tubular ring. The shape of this vortex is identical to the scroll ring, a spiral from the first half-cycle, with the difference that this vortex is hollow on the inside, and the scroll ring has spiral arms rotating inward (although it might be that at some point this vortex is an encapsulation of a scroll ring). This vortex is shaped like a thin hollow torus. The tubular ring is a rotational vortex.
Two examples of tubular rings are bubble rings (mesocyclic) and smoke rings (mesocyclic)
Bubble Rings

Image by Christian Haugen, under CC BY 2.0 license. Image was
cropped
I first thought that bubble rings were scroll rings, thus spirals from the first half-cycle. Only later I learned about the existence of a higher vortex class and the difference between a scroll ring and a tubular ring. An unmorphed tubular ring is very thin. When a vortex ring is thicker you know that it is a lowmorph tubular ring. Most vortex rings that we observe in our world are morphed scroll rings or tubular rings. I still haven't found a perfect way to determine whether a scroll ring or tubular ring is almost or fully unmorphed. There is still some guessing involved.
Smoke Rings
_UnderCCBYSA3.0.jpg)
A smoke ring, formed with a smoke chamber at Bonn
University. Image by Traitor (Wikimedia), under
CC BY-SA 3.0 license
The story here is much the same as with the water rings. Here too we can see rings in a variety of thicknesses. Some very thick, almost like a donut, others very thin. The ones closest to being an unmorphed tubular ring are the thin smoke rings.
One should avoid saying that all smoke rings are tubular rings, because some of them are scroll rings instead. This might be the consequence of the type of smoke used to make such a ring, or a different factor like temperature or environmental conditions might play a role.
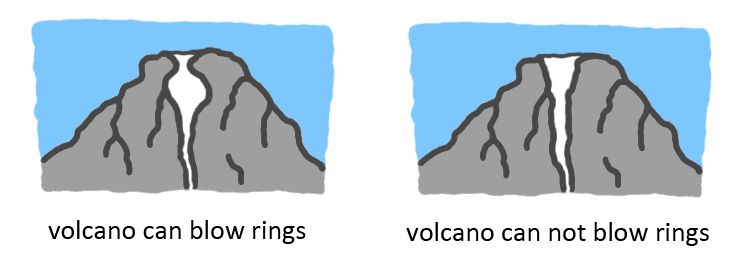
The way that smoke ring generators produce vortex rings is also the same reason why some volcanoes can spew vortex rings like in the video of an Etna eruption shown below. It depends on the shape of the hole in the volcano whether it is possible to do that.
What you need is a cavity below a narrow mouth that will behave like a bulb vortex. Most volcanoes do not spew rings so most probably do not have a bulb. But there might be other factors too that the volcano requires to make these rings. In the case of the vulcano, the rights might more likely be scroll rings instead of tubular rings. It probably depends on the type of smoke which of the two vortex types appears when blowing a ring. Cigarette smoke is higher dimensional than smoke from a wood fire. You can see that by the way that the smoke moves.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |



