The Disks

Disks are flat circular vortices within the third half-cycle, when a spiral with one arm from the first half-cycle dilates, it changes into a disk. Dilation is a type of morphing in which a vortex morphs into a vortex one cycle higher in the transformation sequence. Only when the spiral has one arm, the morph process will result into the formation of a disk. When the spiral has two arms, then the dilation results in the formation of a bell vortex.
DILATION OF A SPIRAL WITH ONE ARM TRANSFORMS THE VORTEX INTO A DISK
DILATION OF A SPIRAL WITH TWO ARMS TRANSFORMS THE VORTEX INTO A BELL VORTEX
I am not 100% sure about this, but I think that a disk morphs towards the position of the high end of a spiral while a bell morphs towards the position of the low end of the spiral. The dimension levels indicated at each of the disk vortices on this page are based upon this assumption. It might be needed to be corrected later if this assumption proofs to be incorrect.
Do not confuse the name of this vortex class with the name of the disc spiral. The disc spiral is one vortex type from a whole different class. I named the disc spiral long before I knew about the existence of the disks. To avoid a mix-up of the names I spelled the vortex type with a 'c' and the vortex class with a 'k'.
There are six known types of disks. The hyperbelt, the mercury belt, the lentillion, the capillion and the mirage. The basic shape of this class of vortices is a round disk, sometimes with a hole in the middle which in case makes the shape more annular. The direction of movement in a disk is uncertain. Only for the hyperbelt and the mercury belt we know that the direction of the sum movement is circular, the rotation goes in one single direction. Likely the direction of movement for the other disks is circular as well, yet in two opposite directions simultaneously, so therefore the rotational movement can not be detected in the sum movement of the vortex.
Disks are the state of equilibrium for metals. Although it is not certain whether all types of metal have a state of equilibrium that is a disk, it could be that bells are also states of equilibrium for other types of metal. What is likely however is that all the metals reside within the third half-cycle, yet it is not known at this moment what all the possible vortex types are that exist within that third half-cycle. What is also not certain is if these states of equilibrium belong to metal ores or pure metals. The correct answer might be metal ore because disks are likely to have two ends of equal dimensionality thus can probably not oscillate. A vortex needs two ends of unequal dimensionality level to be able to oscillate. And since pure metals are able to oscillate, this could mean that pure metals are influenced by a second state of equilibrium, a second vortex, that enables the material to oscillate. Most likely this vortex is the disc spiral. On the page about the state of equilibrium it is explained why.
All the disk vortices on this page are certain to exist, except for the hyperbelt. That vortex has only one observation and that one is with some doubt. There should be at least one full disk at that location the sequence, if its not the hyperbelt than there should be another vortex at that same location that might look different.
Metal Detectors

One clue that provides us with the link between these disks and metal as a material are metal detectors. The detector coils on these devices have shapes that are closely similar to the disk vortices within the third half-cycle. These detectors can also provide us with extra clues that point to more possible types of disks that could exist within the third half-cycle that haven't been identified yet, including different variations of known types, like single and double versions.
Throwing Toys
Another important clue for finding the correct shapes of multiple disk vortices are throwing toys. The most effective throwing devices are all shapes of disk vortices. The image below shows three such examples.
The fourth example, the throwing ring, is not a disk but an interior tunnel, the gyroduct. It is a shape that is quite stable when thrown, yet it can not be thrown as far as any of the three disks. This ring can not be a tubular ring because of its direction of movement. So therefore it must be a different type of vortex, it must be a gyroduct because its the only remaining possible shape that matches. Therefore it also reveals that the sum movement of the gyroduct is a circular movement that flows in the direction of the ring. This is a logical movement for the gyroduct because when a gyroduct forms within a revolute, one of its spiral arms moves inward towards the gyroduct while the other spiral arm moves outward away from the gyroduct. If the gyroduct would rotate into one of the directions of one of the spiral arms than the movement could not progress into the opposite rotating spiral arm. Yet it can in this scenario because the movement is perpendicular to that of both spiral arms.
Morph Sequence
Just as all the spirals within the first half-cycle of the transformations sequence form one complete morph sequence, so do the disks in the third half-cycle form one complete morph sequence as well. Every disk in the sequence can morph into the next disk in the sequence, each step is a transversal of two full dimension levels.
Hyperbelt

| Classification | First disk of the first cycle |
| Dimension | 1.25D |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | No |
| Rotational sum movement | Yes |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | Hyper because of all the disks one can create a throwing toy from, this throwing toy is the fastest. Hyper refers to the word hyperspeed. Belt because it has an annular shape like an asteroid belt or the Kuiper belt |
The disk vortex that loops at the same constant dimensionality level of 1.25D at the third half-cycle (second cycle) is called the hyperbelt. The vortex is shaped like an annular ring that consists of multiple individual rings. The entire vortex lies on one plane and is completely flat. The vortex has no periphery when it is unmorphed, so therefore it is not visible with the naked eye. Only when the vortex is a highmorph vortex it becomes a visible vortex. The hyperbelt is a rotational vortex.
The hyperbelt can be formed by the dilation of a disc spiral. Yet this does not imply that all hyperbelts are the result of a dilation that occurred somewhere during their lifespan. Disk vortices can also be created without the process of morphing. There is only one possible observation so far of a hyperbelt, and that observation are planetary rings.
Planetary Rings

Image by NASA / JPL / Space Science Institute
Some planets within our solar system, which are particularly the gas giants, have planetary rings. These gas giants are Saturn, Jupiter, Uranus and Neptune. The rings are made up of rock, ice, and dust particles that range in size from microscopically small to the size of a house. It is thought that some of the rings might come from moons torn apart by the planet's gravity, or they could have formed as the planets formed. In 2008 the Cassini spacecraft found evidence of the possibility of rings around Rhea, one of Saturn's moons. But the most famous planetary rings are without a doubt those of Saturn itself, which are by far the most visible and spectacular planetary rings within our solar system.
I assume that the rings of Saturn and those of other gas giants are hyperbelts, thus a disk vortex that can form from the dilation of a disc spiral, yet I'm not completely sure about this. The main reason for this is that the annular ring is shaped by countless individual rings, at such a high number such that it is not likely that those rings represent the spiral arms which the spiral dilated from, although it could be that dilation has increased the number of meridians (number of individual movements) of the vortex at such a rate that those countless rings have formed from only a moderate number of spiral arms.
It is to be expected that there exists a disk vortex at 1.25D. And that it is likely that the vortex does not have a periphery, thus is only electromagnetic and can not be seen when it is unmorphed. If these planetary rings are indeed the disk vortex at 1.25D then these rings are a highmorph disk vortex, because these planetary rings are visible to the naked eye (assuming the view is close enough to be observed). It could be that all the planets have these rings, but that the planet's that are no gas giants have rings that are unmorphed, thus are not visible even from close by.
I initially named this vortex type the Huygens belt because of these planetary rings. Galileo Galilei was the first person to observe these rings around a planet in 1610, yet it was Christiaan Huygens in 1655 who first suggested that the shape of this object might be that of a thin flat ring. It might have been a bit unfair for Galileo to name this vortex the name of Christiaan Huygens. Because of the difficulty of choosing between the two I decided to choose neither of them and choose a new independent name instead.
Mercury Belt

| Classification | Second disk of the second cycle |
| Dimension | 2.25D |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Mercury Organic: Unknown |
| Origin of the name | Mercury because its state of equilibrium is mercury (planet Mercury does not have planetary rings). Belt because its shape is like an asteroid belt or the Kuiper belt |
The disk vortex that loops at the same constant dimensionality level of 2.25D at the third half-cycle (second cycle) is called the mercury belt. The shape of this vortex is that of a thick annular ring. I am not sure how thick the basic shape of this vortex should be, the image above is more like a rough estimate. Unlike the hyperbelt, this vortex does have a periphery, so therefore it is visible to the naked eye. The mercury belt can be formed by the dilation of a swirl spiral with one arm, or by the sequential morphing of a hyperbelt. The mercury belt is a rotational vortex.
The state of equilibrium for mercury is the mercury belt, hence this is why I decided to name this vortex the mercury belt. When you place a small amount of mercury in a small cylindrical container, and spin it around a couple of times, the liquid metal takes on the form of a belt. The state of equilibrium for a substance is the vortex whose characteristics are what determines characteristics of that substance. A substance wants to behave like the vortex that is its state of equilibrium. Mercury wants to behave like a mercury belt (more about this is explained on the page about state of equilibrium).
_UnderStandardYoutubeLicense.jpg) Screenshot from Youtube video by Brainiac75 |
_UnderStandardYoutubeLicense.jpg) Screenshot from Youtube video by Roobert33 |
This behavior is shown in the first of two videos below. The second video shows how mercury behaves when subjected to a magnetic field generated by a ring magnet and an electric conductor (the second video will play after the first video as a Youtube playlist). The magnetic field induces the mercury to rotate in circles which reverses direction by changing the polarity of the magnet.
Mercury is also the name of a planet, and this vortex looks a bit like planetary rings, which also form an annular shape. But the planet Mercury does not have planetary rings, so therefore the name 'mercury belt' does not create any conflicts with other existing phenomena.
Two more examples of mercury belts are asteroid belts (macrocyclic) and galaxy NGC 2217 (macrocyclic).
Asteroid Belts
It is not completely certain, but asteroid belts are likely to be mercury belts. It has almost the same shape as a mercury belt, yet it looks like a thicker, more voluminous vortex. This difference in proportions casts some doubt as to whether the asteroid belt is truly formed by the vortex movement of a mercury belt. It could be that the asteroid belt shown in the video below is formed by a highmorph mercury belt, thus a mercury belt that has partly morphed into a lentillion. That might explain why the belt is somewhat more voluminous than one might expect from a mercury belt.
NGC 2217

Image by ESO, under CC BY 3.0 license
NGC 2217 is a galaxy with an outer ring. The outer ring is a lowmorph mercury belt, one that is a morphology between a swirl and a mercury belt. You can still somewhat see the spiral movement in the shape of the galaxy in the photo. This galaxy might once have been a barred spiral galaxy, which has dilation into a mercury belt. It could be that the inner ring is also a mercury belt. The two rings combined could be a double disk, thus a double mercury belt.
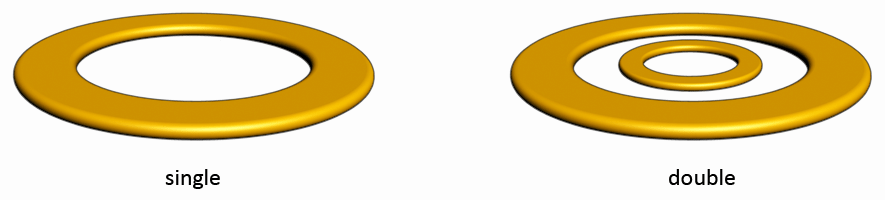
Some metal detector coils suggest that this might be so, double rings might be possible, but then again, this is not certain.
Lentillion

| Classification | Third disk of the second cycle |
| Dimension | 3.25D |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Gallium Organic: Unknown |
| Origin of the name | Lentil because of its lentil shape. The last 6 letters of the word are same as in capillion, which is the next disk in the sequence |
The disk vortex that loops at the same constant dimensionality level of 3.25D at the third half-cycle (second cycle) is called the lentillion. The name of this vortex I chose because of its resemblance with the shape of a lentil. The lentillion can be formed by the dilation of a bulb spiral with one arm, or by the sequential morphing of a mercury belt. The lentillion is a non-rotational vortex.
I am not sure what the basic proportions of a lentillion should be. It could be that the basic shape should be flatter than the one in the image above. I chose the proportions which two of the three examples show. Three examples of a lentillion are the sombrero galaxy (macrocyclic), (some) supercell clouds (mesocyclic) and a hang drum (mesocyclic).
The Sombrero Galaxy

Image by NASA/ESA and the Hubbe Heritage Team (STScl/AURA)
The Sombrero Galaxy is a galaxy with a bright nucleus, an unusually large central bulge, and a prominent dust lane in its inclined disk. The dark dust lane and the bulge give this galaxy the appearance of a sombrero. The Sombrero Galaxy is said to be an unbarred spiral galaxy, but the dust lane looks more like the shape of a annular ring.
The outer ring of the Sombrero Galaxy, the dust lane of the galaxy, is a Mercury Belt. The central bulge, which partly overlaps the dust lane, is a lentillion. Those vortices are both there because the mercury belt is morphing into a lentillion. It is somewhat the same as when a swirl spiral morphs into a bulb. The bulb starts to form at the center of the spiral, and growths outward and becomes more prominent in appearance as the spiral arms shrink to a shorter length until they both completely disappear.
Hang Drum

Image by Michael Paschko, under CC BY-SA 3.0&nbslicense
The Hang is a musical instrument constructed from two half-shelves of steel sheet. It has a unique sound quality, and it is typically played resting on the player's lap. The instrument is the result of years of research and experimentation by its creators. You can hear the sound of the instrument in the video below.
The reason that this instrument produces such a unique good sound is that its shape is that of a lentillion. The lentillion is the result of a dilation of a bulb vortex, and a bulb vortex is the vortex that is located exactly on the central balance point. So this vortex too is located exactly on the central balance point, but the central balance point of the third half-cycle, instead of the first half-cycle. All sound that humans can hear comes the region of the sequence close to the central balance point. This and more things about sound is explained op the page about sound.
The sound of the Hang is more dreamy, sort of a spiritual type of sound. This could be a sound characteristic that is more specific to the higher dimensions, the higher cycles of the transformation sequence.
Supercell Cloud

Not all supercells looks like the one in the photo above, some of them do. This supercell cloud is a lentillion, yet the shape of this cloud is not completely identical to the shape of a lentillion. This is because this cloud is a lowmorph lentillion, thus a vortex that is a morphology between a mercury belt and a lentillion. You can see that the most outer edge of the cloud is a flat disk. That part of the cloud is still close to the shape of the mercury belt while the more inner part has morphed into the shape of the lentillion.
Cumulonimbus Cloud

Image by Mr. Herbert Campbell, for NOAA
A cululonimbus cloud is a dense cloud, formed by water vapor carried by powerful upward air currents, often seen with thunderstorms or during atmospheric instability. These clouds do not always similar in shape, cumulonimbus clouds can be of a few several different types, but these types are located closely to one another within the transformation sequence. The cumulonimbus cloud you see in the image above is one that is formed by a lentillion. These clouds can develop from cumulus congestus clouds (when morphing from bulb to lentillion), or they can develop into a supercell (also shaped by lentillion).
Capillion
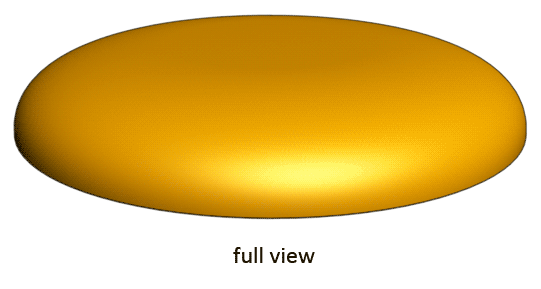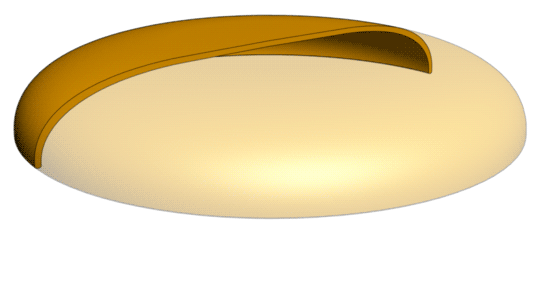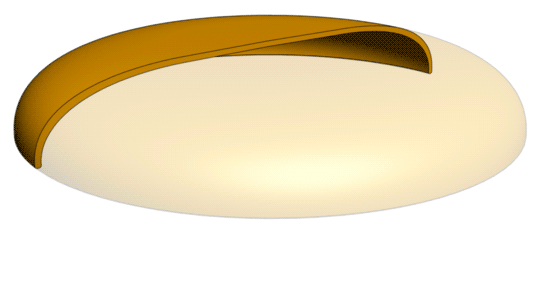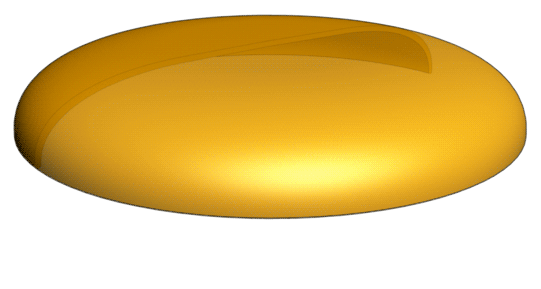
| Classification | Fourth disk of the second cycle |
| Dimension | 4.25D |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Unknown |
| Rotational sum movement | No |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Tin Organic: Unknown |
| Origin of the name | Cap because the vortex has the shape of a cap. The remainder of the word is equal to the last 6 letters of the lentillion, which is the previous disk in the sequence |
The disk vortex that loops at the same constant dimensionality level of 4.25D at the third half-cycle (second cycle) is called the capillion. Its shape is that of the head of a mushroom, almost flat at the center and rounded at the outer ends. The capillion can be formed by the dilation of a revolute with one arm, or by the sequential morphing of a lentillion. The capillion is a non-rotational vortex.
When a lentillion morphs into a capillion, the underside of the vortex gradually becomes hollow, starting at the outer edges, then gradually becoming more hollow at the center as well. The upper half changes in shape as well. While the upper half of the lentillion has an arc shape with no straight section, the capillion is partly flat at the top, with only the outer edges being curved.


Not much is known about this vortex, but more about this vortex is shown on the page about biological life. There you will find some of the connections that explain how the shape of this vortex was determined, and how the vortex morphs.
Mirage

| Classification | Fifth disk of the second cycle |
| Dimension | 5.25D |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | Unknown |
| States of equilibrium |
Inorganic: Silver Organic: Unknown |
| Origin of the name | It is named mirage because this is the vortex that causes the optical phenomenon known as a mirage |
The disk vortex that loops at the same constant dimensionality level of 5.25D at the third half-cycle (second cycle) is called the mirage. The shape of this vortex is that of a flat circular plane, which can be perfectly flat, but is not so in all situations. When you encounter this type of vortex, it is possible that the edges won't be well defined. In some cases the vortex is perfectly round, yet in other cases its edges do not form a geometrical circle. The mirage is a non-rotational vortex.
An interesting feature of this vortex is that it can create a mirror effect, if it lacks the number of required meridians to form a full vortex. When a certain number of meridians are lacking, the vortex can not be anything else but completely flat, with no curvature at all. The vortex will then reflect light as a mirror. Water for example has a number of meridians that is lower than the required number of meridians for this vortex. When a mirage forms in water, it gives a light reflective effect, which is why a lake of water can reflect light.
Examples of mirages are lenticular clouds (mesocyclic), Liesegang rings (mesocyclic), surface tension (mesocyclic) and inferior mirage (mesocyclic).
Lenticular Clouds
Lenticular clouds (Altocumulus lenticularis) are clouds that form in the troposphere. They are a unique type of cloud that usually forms around hills and mountains,as a result as to how the air moves.
 Image by the U.S. National Oceanic and Atmospheric Administration |
 Image by Xperience (Wikimedia), under CC BY-SA 3.0 license |
One interesting thing about lenticular clouds is that they look like they are perfectly stationary and frozen in time. The reason for this is that these clouds are mirages, and mirages are very high dimensional vortices, close to an upper EM crossing location (a crossing location near the higher end of a half-cycle). In the higher dimensions time runs slower, that is why the movement of these clouds is very slow. Those clouds are also quite large, making them even higher dimensional. High dimensional vortices are also less tangible, wind currents do not affect these clouds as much as with most other clouds.
In the right upper image, there are two disks right on top of each other, twice. It could be that those two disks form a double disk, if any of such a disk type configuration is possible. It is not certain, but it is possible that all disks can form both a single and a double version, just as the spirals can.

Liesegang Rings
_PublicDomain.jpg)
Image by DonSiano (Wikimedia)
Liesegang rings are visual formations seen in many chemical reactions that undergo precipitation (separation of a substance from a solution as a solid) under certain conditions. The reactions is often performed within a test-tube into which a gel is formed that contains a solution of one of the reactants. One such reaction is a silver nitrate potassium dichromate reaction.
Some Liesegang rings are mirages, other Liesegang rings are higher dimensional vortices. The rings can be a morphology in between a mirage and a higher dimensional vortex. The first test tube on the left in the image above shows a series of mirages, stacked on top of one another.
Surface Tension
 Image by Yinan Chen |
.jpg) Screenshot from video by Timothy Sleight, Youtube |
The surface tension on water is a vortex with the characteristics of a mirage disk with a lacking number of meridians. This low number of meridians is what causes the surface tension. The low number of meridians also makes the vortex lower dimensional, drawing its position closer to the EM spectrum, and gives the vortex the visual effects of a mirror. The image on the left above shows how the surface of water can reflect the volume of space right above that surface.
The state of equilibrium for water is the swirl. The characteristics of water are driven by the characteristics of the swirl. Water has a number of meridians that is lower than the required number of meridians for a mirage vortex, thus the mirage vortex that forms on the surface of water therefore can not attain the required number of meridians. The reason that the swirl and the mirage are two vortices that share this type of bonding, one being the shell of the other, is for the same reason as some other observations where a vortex is formed within another vortex that is six dimension levels higher than the other vortex. A swirl can form itself within scroll/tube ring, a disc spiral can form itself within a revolute/revodome, light can form itself within a bulb/vessel (think about the light bulbs, or the reason as to why elliptical galaxies are so luminous). Here it is the combination of the swirl with the mirage, one being six dimension levels higher than the other, yet both in a different cycle.
This vortex relation is also shown in Mercury, which you can see in the bucket of mercury in right image above. Mercury has a strong surface tension, and when flattened out its surface is very reflective, a mirror all by itself. Mercury is on the same dimension level as water, except it is located one cycle higher than water. Again, mercury and the mirage vortex are separated by six dimension levels.
Inferior / Superior Mirage and Fata Morgana
_PublicDomain.jpg)
Image by Brocken Inaglory (Wikimedia)
An mirage is known as an optical phenomenon that may appear as a lake of water in the distance that reflects the objects that are located right above that surface. Basically the mirage behaves like a horizontal mirror stretched out in the distant landscape. There are three types of these optical phenomena: the inferior mirage, the superior mirage, and the fata morgana.
This reflective effect is caused by a mirage vortex that floats closely above the ground. When a mirage lacks the required number of meridians it becomes more planar due to a lack of freedom of movement and at some point, perhaps under some additional conditions, the vortex starts to behave like a mirror by reflecting incoming light. In the case of a fata morgana, multiple of these mirage vortices are stacked on top of each other.
Both silver and aluminum can be used to create mirrors, so it could be that there are more vortices, closely within the same location within the transformation sequence, that can cause this same phenomenon.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |





