The Color Spectrum

Occurrence of Spectral Colors

What I've noticed is that all phenomena that produce spectral colors are also phenomena where movements diverge in exact opposite directions on a very thin transparent surface. This divergence can be both single axial (two directional) and double axial (circular), in which case the double axial variant is a higher dimensional movement than the single axial variant, and requires a higher dimensional medium than the single axial variant.

It is important to understand that these colors only occur when the surface is very thin / flat. And the medium in which this movement takes place must be a transparent medium. So far, air, oil, water mixed with soap and light are mediums that are known to be able to produce this phenomenon.

The reason why this effect only occurs when the surface is very this is because this effect is caused by the core movement of a vortex, and not by the peripheral movement. The core of a vortex is an electromagnetic movement and does not have any volume. The thinner a vortex becomes, the more closer its movement is located at the EM spectrum line of the transformation sequence, thus the closer to the electromagnetic spectrum. If a vortex becomes so thin that its volume is nearing zero, then all the movement of the vortex becomes core movement, and the peripheral influence disappears.

If you take for example the disc spiral, which line line of movement has no volume, and thus the entire movement is an electromagnetic movement. When the disc is a highmorph disc, only then the disc has a peripheral movement, only then it can create (infrasonic) sound waves in air and push and pull on physical matter. Thin vortices with near to zero volume only influence core movement, and the colors that we humans are able to see come from electromagnetic spectrum, which is the core movement of a vortex. So therefore it is logical that color effects can be produced from the movement of these very thin vortices.

The occurrence of spectral colors on thin surfaces can best be made clear by showing a series of examples.

Example #1 - The Prism

A prism is a transparent optical solid which is able to refract light. A prism has at least two flat surfaces that are at an angle. The most common shape is the triangular prism with a triangular base and rectangular sides. When a light beam hits a glass prism at a certain angle, the light splits into a rainbow pattern. The light beam widens, making a diverging movement. Thus a light beam split by a prism is an example of single axial divergence.

The reason that a prism is able to produce this color effect has to do with the fact that the shape of the prism induces vortex movement that is located very close to the EM spectrum line of the transformation sequence, thus very close to the electromagnetic spectrum. This comes from the fact that a triangular prism is a dedimensionalized hyperkone. The movement of a hyperkone lies very close to the zero point and very close to the electromagnetic spectrum, the movement of a dedimensionalized hyperkone is even lower dimensional, thus it is located even closer to the electromagnetic spectrum.

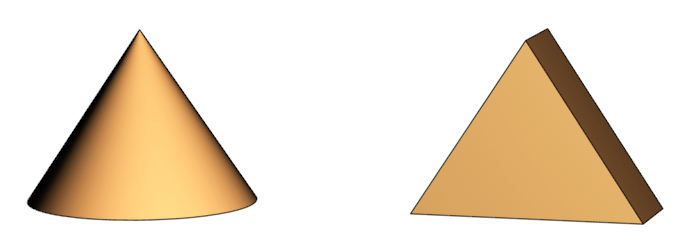
triangular prism = dedimensionalized hyperkone

The state of equilibrium for diamond is the hyperkone (an angular hyperkone, thus one with a reduced count of meridians). Diamond too can disperse white light into multiple spectral colors. The reason as to why diamonds are treasured for their optical beauty has to do with the ability as to how these gems are able to disperse light. No other positive dimensional vortex lies closer to the electromagnetic spectrum than the hyperkone.

This triangular dedimensionalized cone shape sometimes appears on the surface of uncut diamonds that are formed by natural processes. This is where we can recognize the shape of the prism. A hyperkone can not form itself inside the volume of a diamond, but it can form itself at the edge of a diamond, where that medium touches another medium (air or some mineral different than diamond). Same holds true for water, a swirl can not appear submerged in water, but a swirl can appear at the surface of water, where that medium touches another medium (air).

Image by Gump Stump (Wikimedia), under CC BY-SA 3.0 license

One face of an octahedral uncut (rough) diamond, including scale. Note the trigons on the diamond surface. The diamond is 0.9 carats, white (approximately GIA 'E' grade), with no significant internal inclusions. Taken on a Leitz Laborlux 12 Pol polarizing transmitted light microscope, using a Diagnostic Instruments Inc. SPOT Insight 2MP Color Mosaic digital camera [text from Wikipedia].

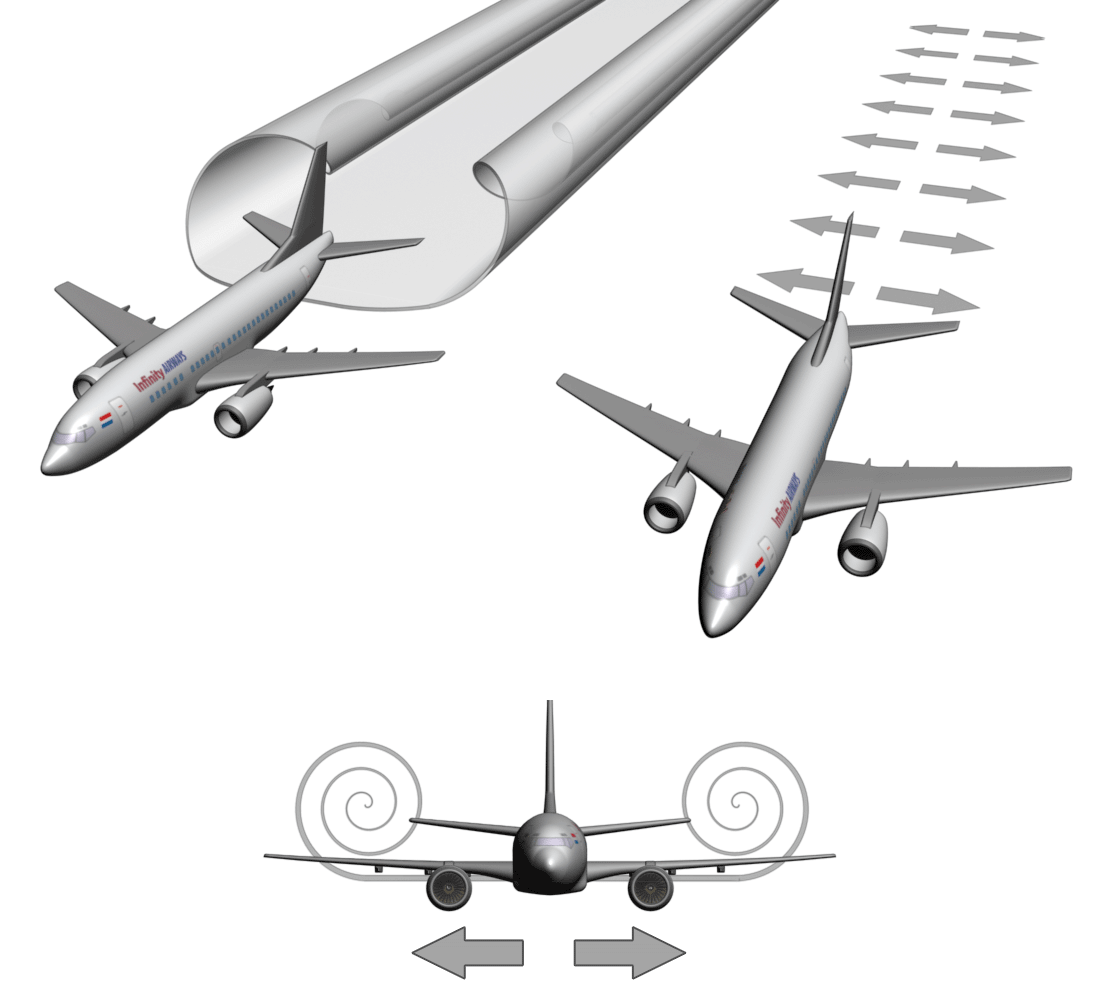
Example #2  -  Vortex Wakesheet behind an aircraft
 

Image by Sean Stayte, under CC BY-NC-SA 2.0 license. Image contrast was altered to accentuate the spectral colors.

Image by Maarten Visser, under CC BY-SA 2.0 license

The vortex wakesheet behind an aircraft is a wake belt with a scroll at either side (binary scroll). This was mentioned on the page about the outer bridges. The wake belt sometimes produces spectral colors, like those you can see in the image above. The exact conditions for these spectral colors to occur is something I don't know, but I can give the most important condition that is needed for these spectral colors to occur.

The spectral colors appear because of the directions of the movements in the wake belt and the way that the vortex wakesheet is formed. The wake belt is a very thin sheet in which the movements point in exact opposite directions. This pulling apart of the thin sheet in these opposite directions is what creates the spectral colors. The wakesheet is an example of single axial divergence.

Example #3  -  Soap Bubbles

The man in the photo above is SamSam Bubbleman. Holder of several world records which are all about... you guessed it: bubbles! Notice that these bubbles produce a wide range of colors from the entire color spectrum.
 

Image by Brocken Inaglory (Wikimedia), under CC BY-SA 3.0 license

A bubble has a very thin outer surface. When you blow up a bubble, its surface stretches out. Different positions on the surface move apart from each other. A bubble is an example of double axial divergence. This divergence requires a higher dimensional medium than single axial divergence. Water is not high dimensional enough to complete such a movement. With just water you cannot make good bubbles. In this case, it is the soap mixed in the water that makes it higher dimensional. If the surface of a bubble would be thicker, than no color spectrum would show.

Example #4  -  Oil Spill

Image by John (Wikimedia), image was converted to GIF
and arrows added

Just as soap is high dimensional, so is oil. In this picture, oil makes the movement of the belt and thereby produces spectral colors. If this was water, no spectral colors would appear, because water is centered around the swirl, thus is too low dimensional to complete such a movement.

If you have doubts whether this is true, if you think that water can make this same kind of movement, then all you need to do is a simple test. Find a flat solid surface and then steadily poor water on it. You will observe that diverging movement that the water makes only reaches a small radius and then starts to protest. But if you do the same thing with oil, the diverging movement reaches a much larger radius without any disruption. This is because oil is higher dimensional than water, and it contains more individual movements (meridians).

Example #5  -  The Morning Glory Pool

Image by National Park Service employee, U.S. federal government

Morning Glory Pool, one of the most popular and beautiful pools in Yellowstone National Park, earned its name in the 1880's due to its deep blue coloration and likeness to the Morning Glory flower. The morning glory pool is a hot spring that on a few rare occasions has erupted as a geyser, usually following an earthquake or other nearby seismic activity. The pool is famous for its bright colorful appearance which has changed over the years from blue to yellow and green.

Image by Jon Sullivan. Image was edited with text, arrows and canvas size.

The reason that the spectral colors pop up here is because of the flow of the water and the shape of the cavity. The warm water flows upward to the surface and then outward from the center. In this case, the plane is the water surface and the divergence is a double axial divergence. Because it is double axial it requires a higher dimensional medium to complete the expansive movement. We already know from the soap bubble example that normal water is not high dimensional enough to complete such a movement. So what is that makes this water different from the water in most other pools and lakes?

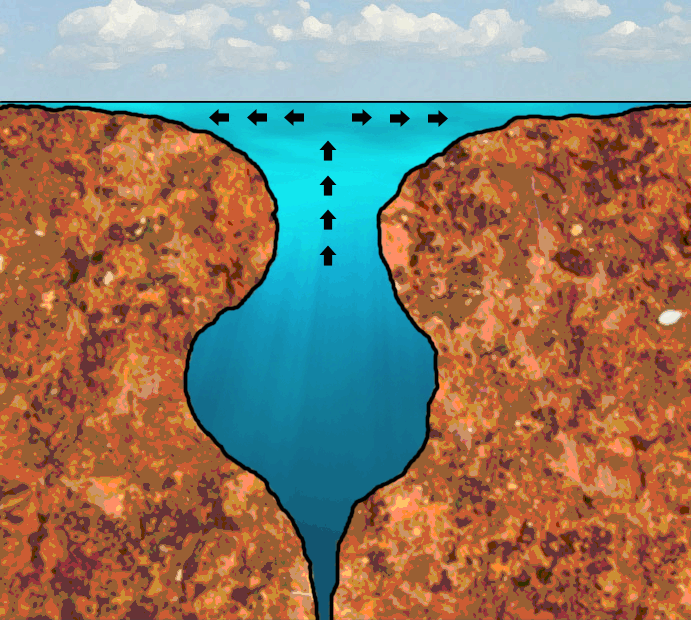
The answer lies in the geometric shape of the cavity below the water surface. If you look at the first photo, than you'll notice that there is a cavity down in the depths of the pool. There is probably some kind of a cave beyond that narrow opening. What I suspect is that there is a cavity down there that acts as a bulb. On the page about state of equilibrium we discussed how water is centered around the swirl (the swirl is the state of equilibrium for water). For water to correctly increase in dimensionality, it first needs to pass an amplicone, then a bulb and then a revolute. That is what is does here, because of the shape of the pool.

What I'd like to know is if the color is mostly at the surface of the pool. If you would dive into the pool and swim downward, would you see any strange colors?. Or would it look like normal color rock and water?

Volcanic Lakes
 

Image by United States Government from National Park Service

Image by Wikiwanito (Wikimedia), under CC BY-SA 3.0 license

Another example in the same category as the morning glory pool are volcanic lakes. There are several volcanic lakes on our planet that show unusual colors. In some cases the color completely changes overnight. The explanation for the occurrence of these colors is the same as that of the morning glory pool. A question that arises here is if the higher temperature water is among one of the conditions required to achieve such colors. The water in these lakes has a higher temperature than usual, higher temperature means lower dimensionality (more yang) on the microcyclic scale, which gives the reaction of higher dimensionality (more yin) on the mesocyclic scale. Higher dimensionality is required to perform double axial divergence. So hereby it is likely that the increase in temperature is one of the required conditions to achieve such colors. Shallow water might also be a required feature of the lake.

Now, the current scientific explanation for the colors in these volcanic lakes is that bacteria in the water make the water look colored. The big question here is, is one of the two explanations the correct one? Or are both explanations correct? It could it be that because the water becomes higher dimensional, it thereby becomes more suitable to sustain life? It should be possible to perform simple experiments that could proof whether this is correct.

Scaling (Growing and Shrinking)

Now, what do these observations tell us about the exact meaning of color? If we look back on what we now know about temperature, how temperature is one thing that gives us information about reactions that take place in the microcyclic scale level as a direct result of actions that take place in the mesocyclic scale level, then we can assume that there are more things that might give us information about what is happening in the microcyclic scale level.

We saw in the page about temperature how one action creates a reaction. When dimensionality on one scale level increases, then it decreases in a lower scale level, and vice versa. When we look at these four examples on this page, we see that in each example the vortex movement is outward, it appears that the vortices are scaling, they are growing to a larger size.

If you look at the four examples, you see that the shape of the vortex in which these spectral colors appear stays pretty much the same. The shape of the vortex sheet behind the aircraft stays rectangular, it just grows wider. The shape of the bubble stays round, it just grows bigger. The shape of the oil spill maintains its annular shape, it just grows bigger and bigger, same as the movement on the surface of the morning glory pool.

These vortices are not progressing from one vortex in the sequence to the other, but they are growing in scale size. And we already know that when dimensionality increases on one scale level, then dimensionality decreases on another scale level. One action produces an opposite and equal reaction. So then it also could be true that if the scale size increases in the mesocyclic scale level, then the scale size in the microcyclic scale level decreases. It could be that this change of color indicates a change in size of the microscopic vortices, thus an opposite reaction in the microcyclic scale level.
 

COLOR = THE SIZE OF THE VORTICES ON THE MICROCYCLIC SCALE
 

You need to think about the logic behind this. We can see with our eyes how large vortices are in the mesocyclic scale level. They range from very small to very large, from nothing but the size of a grain of sand to a large tornado. We can see how large some of the vortices on the macrocyclic scale are when we look at the sky. There we see the sun and the moon. Once we learn about their distance to our earth we can also perceive how large they are. If we would be able to travel outside of our galaxy with a spaceship, and glance through a window, then we would be able to see the massive size of our Milky Way.

But everything within the microcyclic level is beyond our visual perception unless we use a microscope. It does not make a difference whether a vortex is microscopic in size or nanoscopic in size. We simply can not see the difference in size because we can not see neither of them. So this is where color plays its part. Color reveals the scale size of the vortices that are too small for us to see.

Now, I've also told you that I'm not 100% sure about this. The most reason for doubt is that the different colors suggest different levels / steps or states. Scale size does not answer to that. You have to keep in mind that the definition that I just gave you is still prone to error. But I am convinced that we are getting close to the correct answer. Perhaps we are not there yet, but we are looking in the right direction.

Brightness

Another property of color is brightness. From the yin yang point of view, lighter colors are more yin (higher dimensional) and darker colors are more yang (lower dimensional). But just as with the color spectrum, we do not know in what way lighter colors are more yin and darker colors are more yang. Some information that should be important is lacking here. Crystals can have very light colors, but crystals are very low dimensional on the mesocyclic scale. And petroleum has a very dark color, but is high dimensional on the mesocyclic scale. This suggests that brightness too, just as color, could be an indication of some condition within the microcyclic scale level.
 

To find out what brightness of objects indicates, we need to look at phenomena that show the two possible extremes of brightness. Those are the things that are very dark and the things that are very bright. For that we take a look at a third variant of divergence. Namely triple axial divergence.

Triple Axial Divergence

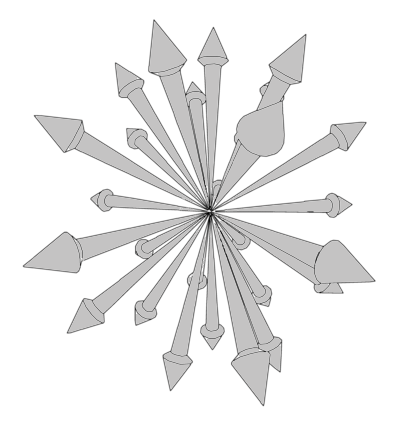
A vortex can make a diverging movement in the direction of one or two axes, but it can also make a diverging movement in the direction of all three axes (x, y and z) simultaneously. This is called triple axial divergence or spherical divergence. This movement is found in bright light sources and in some crystals. But the first clues for this type of movement I found in plant life. Some flowers show this shape of movement, and it are those flowers that nearly always show bright colors. The color can be any kind of color, but the most prominent is white.

Flowers and other vegetation are one source where we can find this kind of movement and shape. The rays of the sun, which to our human eye looks white, also makes this kind of diverging movement. The brightness that goes along with the shape is an important clue that helps us with a little push in the right direction.

(The picture at the bottom left is something called tiptopite. It is not microcyclic but very small. The water tentacle thingy in the picture next to it is called hytoplankton (cyanobacteria)).

I did find one exception in nature about this observation in color. And that is the sea urchin. Sea urchins are mostly dark colored, some are very dark. And these sea urchins do have this similar star-like shape. The difference in shape in that the outer shell at the center of the sea urchin is a hollow sphere. The previous examples did not have a hollow sphere at the center.

Image by NOAA

Despite that we are not sure whether these observations truly relate to vortex movement, we do see that there is a relation with color. So there is a good possibility that this too is a type of divergence, and some kind of color reaction that takes place due to scaling or some other movement.

Lets try to think ahead and make a little prediction based on the small things that we know. If an outward movement produces bright colors, then it could be that an inward movement produces dark colors. It could be that black substances like carbon and petroleum are in some ways formed by this type of movement. This is not certain, but it is a logical idea.
 

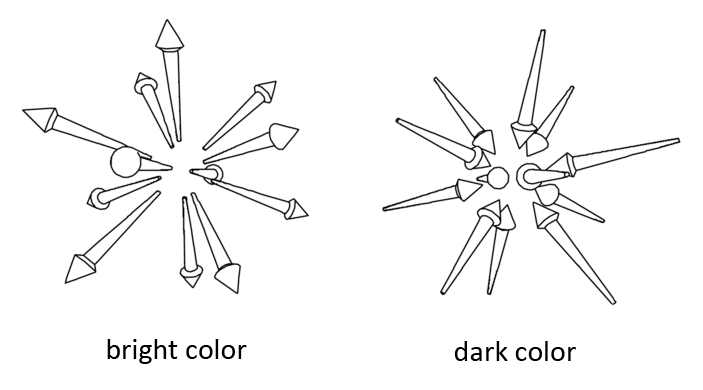
What strikes me most about the movement that produces the bright colors is that that movement is the most yin movement possible. It is the fastest way in which a vortex can expand, the quickest way of making a movement to the higher dimensions. So the quicker a mesoscale vortex makes a movement to the higher dimensions, the brighter its color. Then it could be that the color becomes darker as the movement becomes less yin, where it eventually becomes a dark color that indicates movement in the other direction: contraction.
 

BRIGHTNESS = THE DIRECTION OF MOVEMENT (EXPANSION OR CONTRACTION) OF VORTICES ON THE MICROCYCLIC SCALE
 

White is strong expansion on the mesocyclic scale and strong contraction on the microcyclic scale. Black is strong contraction on the mesocyclic scale and strong expansion on the microcyclic scale. Grey should be something in between. No contraction nor expansion.