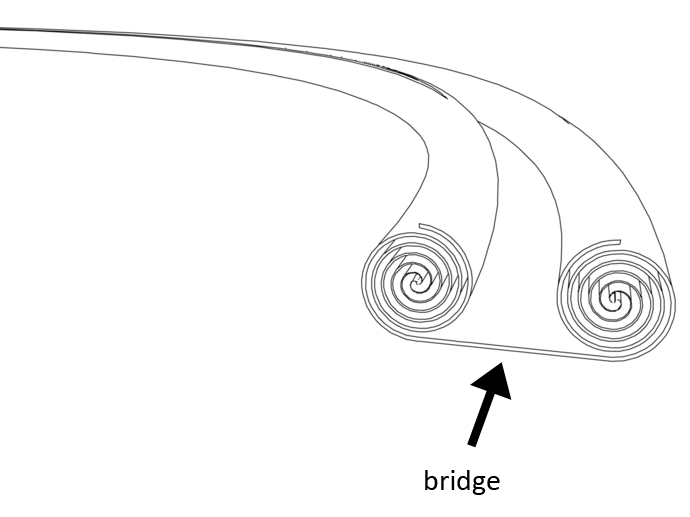
The Outer Bridges
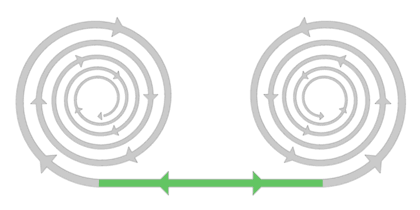
On the previous page we discussed the spirals. Spirals come in three varieties, one of them is the binary variety. A binary spiral consists of two spirals that are connected with an outer bridge, thus a bridge that connects the outer ends of two spirals. Examples were shown of each and every spiral on the previous page but more detail about these bridges will be discussed on this page.
An outer bridge connects the outer end of a left-turning spiral, to the outer end of a right-turning spiral of equal type. Below the central balance point, the bridge connects to the high end of the spiral (disc and swirl). Above the central balance point, the bridge connects to the low end of the spiral (revolute and scroll ring). A bridge has two ends with the same level of dimensionality. In between the dimensionality level also remains the same. The change is in direction of rotation. But the movement does not go from one end of the vortex to the other. Instead the peripheral movement is a movement that starts at the center of the bridge and goes into two opposite directions simultaneously, but there is some doubt whether this is correct. It could be the core that makes this movement, the movement of the periphery could be different, but it does not flow from one end to the other.
This is completely different with the inner bridges. In those bridges, the peripheral movement does flow from one end of the vortex to the other. Inner bridges connect two spiral arms together, not two different spirals. And the spiral arms move in two opposite directions. More about this can be read on the next page, the page about the inner bridges.
So far, five different outer bridges have been found in the positive side of the sequence. All of them have been observed and thus have been confirmed to exist. These are the enexus, the troth, the exobar, the pilaster and the wake belt.
One characteristic of all outer bridges is that they are never seen without the spirals, except when those spirals can not be visible because of them being the state of equilibrium for the medium in which the outer bridge exists (for example, revolutes can not be visible in outer space. This will be explained on the page about state of equilibrium). Apart from that, all outer bridges I have observed so far are connected to a spiral at both ends, I have never observed any of them as a separate vortex without the spirals. This characteristic makes these bridges easier to identify and not easily mistaken with something else. Inner bridges, for example, are most often seen without the spirals, without any of the subsequent vortices attached to them.
Enexus
| Classification | Second outer bridge of the first cycle |
| Dimension | 1.25D (CW<>CCW) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | No |
| Rotational sum movement | No (not 100% sure) |
| Minimum number of movements | 1 |
| States of equilibrium | Organic: Resin |
| Origin of the name | Nexus means 'connection' or 'link'. Nexus is already a name used for a well known smart phone brand, for that reason I added the extra 'e'. |
The vortex that connects the outer end of a left-turning disc spiral with the outer end of a right-turning disc spiral, revealing the presence of a wave with a single constant dimensionality of 1.25D, is called the enexus. The shape of the vortex is somewhere close to a single straight line. In some observations the vortex is bend inwards or outwards. The enexus is most likely a non-rotational vortex, but this is not completely certain. Because the vortex is connected to two discs, it is very likely that it only consists of a core and no periphery.
Below is a photograph of an enexus. In this example, a binary disc is formed by a revolute. The revolute is a vortex 6 dimension levels higher than the disc. The same thing happens when a vortex sheet behind an aircraft, which is a binary scroll, creates a binary swirl (see examples further down). Here again, the scroll is a vortex 6 dimension levels higher than the swirl. So one spiral creates another, less dimensional spiral, whose shape is the cross-section of its own shape. This phenomenon is called 'vortex embedment', and it is discussed on the page titled 'More About Vortices'.

If you look at the photo on the left then you might think that you're looking at a photo of one vortex. But the photo actually reveals two vortices. One is the revolute and the other is the binary disc that is formed by adding the white dye. The white dye is not merely a cross-section of the larger vortex.
How can we be more sure that these are two vortex types and not one? Well that's not too hard. If it is only one vortex that we are looking at and the white dye merely shows a cross-section of that single vortex, than it should also be possible to show a greater part of that vortex using the white dye. You would perhaps be able to show a band or a pie-section of the revolute, instead of a thin line. But I haven't seen any photograph that showed anything like that (if anyone ever achieved doing that, please e-mail me). And I predict that is not possible. The white dye simply forms a new vortex of a specific type within the bigger, less visible vortex. Which is 6 dimension levels lower than the previous. This new vortex is not just a cross-section of the other vortex.
A vortex ring generation geometry that has been cited as a standard consists of the tube exit mounted flush with a wall with the piston stroke ending at the tube exit. We employ this geometry to investigate the effect of the vortex that forms in front of the advancing piston (piston vortex) on the primary vortex ring that is formed at the tube exit. It is shown that when the piston finishes its stroke flush with the wall, and hence forms an uninterrupted plane, the piston vortex is convected through the primary ring and then ingested into the primary vortex. The ingestion of the piston vortex results in an increased ring impulse and an altered trajectory, when compared to the case when the piston motion is finished inside the tube. The photograph, at the instant the piston motion has ceased, shows the primary ring and the piston vortex [Allen, J. J. & Auvity, B. Interaction of a vortex ring with a piston vortex. Journal of Fluid Mechanics 465, 2002, 353-378].
The enexus you see in the picture above is a highmorph enexus. Just like ladders and spirals can morph into subsequent ladders and spirals, so too can bridges morph into subsequent bridges. The two discs the enexus is attached to are also highmorph discs. You can tell that these vortices are highmorphs because these are vortices that have only a core movement, and thus are invisible if they are unmorphed vortices. These vortices are visible, so you know that these discs are a little bit higher dimensional. The discs are partly morphed into swirls.

Formation of a vortex ring from a nozzle. Water is ejected from a sharp-edged circular nozzle of 5-cm diameter into a tank of water by a piston that moves at a constant speed of 4.6 cm/s after accelerating for 0.3 s. The rolling up of the vortex sheet that separates from the edge is shown by dye injected there. The piston stops at 1.6 s, and the vortex ring then induces a secondary vortex of opposite circulation. Didden 1979 [text and image from 'An Album of Fluid Motion' by Milton van Dyke].
Pattern Formation in Electrically Conductive Fluid
Electric and magnetic fields can be used to manipulate the flow movement in a fluid if the fluid is electrically conductive. This can be achieved by inducing a potential difference across electrodes which are placed within the fluid. The field of study that describes the behavior of these kind of magnetic properties is called magnetohydrodamics (often abbreviated as MHD).
What is interesting about this example is that the outer bridges form at both outer ends of each double spiral, thereby the outer bridges and spirals combined form a repeating pattern, going from spiral to outer bridge, to spiral, to outer bridge, and so on. An outer bridge can connect in such a way that it repeats a series of spirals, alternating between left and right-turning spirals. There is also a different type of bridge that can achieve almost the same thing, which is called an s-bridge (s-bridges are discussed on the page page titled 'more about vortices'). The difference between this type of bridge and an s-bridge is that the s-bridge connects spirals that all rotate in the same direction, all left-turning or all right-turning.
Troth
| Classification | Third outer bridge of the first cycle |
| Dimension | 2.25D (CW<>CCW) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | Unknown |
| Minimum number of movements | 1 + 2 |
| States of equilibrium | Organic: Honey |
| Origin of the name | It is named troth so that it represents the connection between two living organisms |
The vortex that connects the outer end of a left-turning swirl with the outer end of a right-turning swirl, revealing the presence of a wave with a single constant dimensionality of 2.25D, is called the troth. The shape of the vortex is close to that of a straight or somewhat bend cylinder. Like the enexus, in some observations it looks bend inwards, in others it looks bend outward. How the path of the individual movements (meridians) look like in a troth is not known. It is also not known wether the sum movement of vortex is rotational or non-rotational. Because it connects to two swirls, it is likely that it has both a core and periphery movement. But if it has a rotational movement in 1 or 2 directions is not known.
Three examples of a troth are: Smoke angels (mesocyclic), hydrogen bubbles in a vortex sheet (mesocyclic) and interacting spiral galaxies (macrocyclic).
Smoke Angel
_PublicDomain.jpg)
Image by Russell E Cooley IV, USAF
This vortex is created by an invisible vortex sheet that forms behind an aircraft. The vortex sheet is a binary scroll. The cloud vortex is a binary swirl. The binary swirl is formed by the smoke trail from the released flares, which form a binary swirl in the cross-section of a vortex sheet. Here the binary scroll (= vortex sheet) is invisible, but the binary swirl is visible. You won't find any real photos of the vortex sheet because the vortex wake sheet is a vortex that is normally not visible in air, it is too high dimensional. There are however simulations of the vortex wake sheet, like in the video below.
Hydrogen Bubbles in a Vortex Sheet
Below are a series of photographs made of vortices that are formed within a vortex sheet behind a rectangular wing taken from 'An Album of Fluid Motion' by Milton van Dyke. Here it's the same story as the binary disc that is formed within a revolute. You might think when you look at these photographs that you are looking at one vortex. If you know that there is one invisible vortex sheet behind the wing then you could assume that this smaller vortex formed by the hydrogen bubbles is a cross-section of that bigger vortex. But that is not quite right. This binary swirl you see here is actually a new vortex of a different type. The scroll ring is a spiral of the tenth dimension level, the swirl is a spiral of the fourth dimension level. So one spiral creates another spiral that is 6 dimensions lower than the first. This is the same principle as with the binary disc formed by a revolute showed in the example earlier on this page.

Cross section of the vortex sheet behind a rectangular wing. The wake rolling up behind a rectangular wing at 9 degree angle of attack is seen at distances behind the trailing edge of 1.0, 1.6, 2.9, 5.5, 11.2 and 21 chord lengths. The wing has a Clark Y section 10-percent thick, a chord of 0.125 m, and a span of 0.3 m, with tips cut off square. It is supported by fine wires and towed through water. The wake is visualized by hydrogen bubbles emitted from a 30um wire located just behind the trailing edge and illuminated by xenon lamps. The vortices separate from the wing surface just behind the mid-chord. The Reynolds number is 100,000 based on chord. The vortex sheet is initially turbulent, but is relaminarized farther downstream. Photograph by H.Bippes [text and image from 'An Album of Fluid Motion' by Milton Van Dyke].
The reason we know that these are two different vortices is because the binary swirl that forms always has the same thickness. If this vortex was really just a cross-section of the vortex sheet than it would be possible to use the hydrogen bubbles to reveal a bigger, wider section of the vortex sheet. Or we would be able to show the entire vortex sheet using these bubbles. But I haven't seen any video or photograph where this is achieved. The vortex that forms is always a thin binary swirl or a series of thin binary swirls.
The reason that hydrogen bubbles gives this effect is because hydrogen is higher dimensional than air (one way you can determine this is by the low weight of hydrogen). Because the hydrogen is high dimensional it has the tendency to contract when the medium around it is lower dimensional, and it finds a chance to do so when it comes in contact with the binary scroll ring, where it contracts as a low dimensional swirl. If the hydrogen bubbles would not have been there, then no swirl vortex would have formed. The reason this also works with clouds behind an airplane must be because these clouds are also higher dimensional than the clear sky around it.

Image by U.S. Coast Guard
Have a moment to look at this professional photo gallery (click). It's a series of stunning looking aviation photos made by Paul Bowen that show vortices that form in the clouds behind an airplane. You can see that the vortices that form behind an aircraft are separate vortices of limited depth. There is no spiral cloud behind the aircraft that stretches further in depth. If you look closely you can almost count the number of swirls that have formed. They all have this same shape and proportions because they are swirls, they are vortices of a specific type, formed within the larger, invisible vortex sheet.
Interacting Spiral Galaxies

All three images by NASA/ESA and Hubble Heritage
Team (STScl/AURA). Images were edited with text
Some interacting spiral galaxies are binary spiral galaxies. A 'binary spiral galaxy' is not a name that existed yet. However, we can introduce that new term here. A binary spiral galaxy are two spiral galaxies connected with an outer bridge, thus as a binary swirl. As far as I know, astronomers haven't named these twin opposite rotating galaxies yet, but refer to them as interacting or colliding spiral galaxies.
There are some spiral galaxies photographed by the Hubble space telescope that are binary swirl galaxies. Unfortunately, in nearly all of the examples the bridge is not fully visible. The only one that almost forms a full bridge is ARP272. To refer to these galaxies as colliding galaxies would be incorrect because these galaxies are not at all colliding. Binary swirls can be found anywhere in our natural world, like for example the swirls on the surface of water, shown in the two videos below (the second video will play right after the first). By observing them we can easily find out that two swirls that rotate in opposite directions never collide, and certainly never merge. Two swirls however can merge if their rotational flow goes in the same direction, both clockwise or both counterclockwise. Same rules apply to these galaxies. You do not need to look in space to find all the answers.
Thread of Honey
A thread of honey is a very viscous fluid whose movement is determined by the movement of a troth. The reason for this is that the state of equilibrium of honey is the troth. This means that honey tends to behave like a troth. A thread of honey can be classified as only the troth itself, thus without the two spirals at both ends. But in that case the ends of the thread do want to behave as two ends attached to the starts of the two spirals.
This spiraling tendency of the end or start of the thread is revealed by the video above. What you see is a thread of a very viscous fluid, like honey, falling on a moving belt. At first the belt moves a fast pace and the thread forms a straight line. At low speeds, the thread of honey zigzags because of its tendency to bend into a spiral. At even lower speeds the thread starts to coil.
Exobar
| Classification | Fourth outer bridge of the first cycle |
| Dimension | 3.25D (CW<>CCW) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 1 + 7 (estimate) |
| States of equilibrium |
Inorganic: Unknown Organic: Pitch |
| Origin of the name | Exo because it is an external bridge, in contrast to the endobar. Bar because of its elongated bar shape |
The vortex that connects the outer end of a left-turning bulb with the outer end of a right-turning bulb, revealing the presence of a wave with a single constant dimensionality of 3.25D, is called the exobar. The shape of the vortex is somewhat like a straight cylinder that is conical at both its ends. Because it connects to two bulbs, it is likely that it has both a core and peripheral movements. But the exact number of movements is unknown. The exobar is a non-rotational vortex.
Three examples of a exobar are binary elliptical galaxies (macrocyclic), creeping flow past two spheres in tandem (mesocyclic), droplets of water in microgravity (mesocyclic) and rotating capillary instability (mesocyclic).
Binary Elliptical Galaxies

Image by Robert Lupton and the Sloan Digital Sky
Survey Consortium
Elliptical galaxies are formed by bulbs. When we look at our universe through the lens of a telescope we sometimes find two elliptical galaxies in close proximity to each other. In between these two galaxies should be a bridge if the pair forms a binary spiral. Unfortunately, while I have found more or less some connections between these ellipticals, I haven't found any image that shows the bridge very clearly. The best is NGC5218 (upper image). The one on the bottom left is called the Hickson Compact Group 90. It looks like it has an incomplete bridge. The one at the bottom right is NGC4676, which are spiral galaxies that are lowmorphs of elliptical galaxies, thus a binary swirl partially morphed into a binary bulb. This is possible because in the morph sequence, the bulb and exobar are subsequent vortices to the swirl and troth.
Creeping Flow Past Two Spheres in Tandem
When two metal spheres are placed close to each other and water flows past these spheres then the flow of water in the space in between the spheres takes the shape of a exobar. The reason for this is because the metal spheres are closely shaped like bulbs, so they act like bulbs. Solid shapes that act like vortices and thus induce the creation of other vortices when a fluid flows past it is something that is observed more often. Other examples are an amplicone created by single metal sphere, a disc spiral created by a cone shaped object and a helicone created by a disc shaped object. These examples can be found on other pages.
_FromAlbumOfFluidMotion.jpg)
With the same spacing and approximately the same Reynolds number as the circles opposite, spheres show no sign of separation. This is consistent with the fact that separation on a isolated sphere appears only above a Reynolds number of 20, compared with 5 for a circle. Aluminum dust is illuminated in glycerine. Tenada 1979 [text and image from 'An Album of Fluid Motion' by Milton Van Dyke].
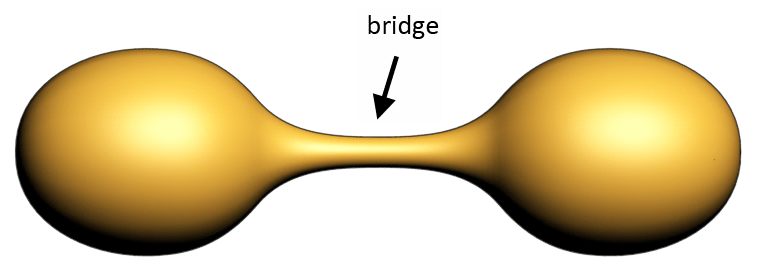
Droplets of Water in Microgravity

Image by NASA
Droplets of water behave somewhat different in the absence of gravity than they do here on earth. Although the shape the water droplet takes on in the image above might be reproduced here on earth, it is less likely to be that easy to create such an symmetrical shape from just water. The photo was taken under microgravity, thus under very low, almost zero gravity. The bridge you see between the two bulbs in the droplet on the right side of the image is an exobar.
Rotating Capillary Instability
This example is one of which I'm not 100% sure if these are indeed exobar vortices. This example is about repeating vortices. Sometimes spirals can repeat themselves in a line which is something that is discussed on the page which is titled 'more about vortices'. These spirals are connected with bridges. I think that the connections you see between the bulbs in the lower picture are exobar vortices, but again, I am not sure about that. It was the best example I could find of two bulbs connected with a exobar at mesocyclic scale here on earth.

Effect of rotation on capillary instability. The instability of the upper jet of water, with excitation at wavelength 4.8 diameters, is increased in the lower photograph by rotating it at 435 revolutions per minute. Rutland & Jameson 1970 [text and image from 'An Album of Fluid Motion' by Milton Van Dyke. Image was edited by adding a zoomed region of the image].
Pilaster

| Classification | Fifth outer bridge of the first cycle |
| Dimension | 3.75D (CW<>CCW) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 1 + 12 (estimate) |
| States of equilibrium | Organic: Petroleum |
| Origin of the name | It is named pilaster because it is shaped like a pilaster |
The vortex that connects the outer end of a left-turning revolute with the outer end of a right-turning revolute, revealing the presence of a wave with a single constant dimensionality of 3.75D, is called the pilaster. The shape of a pilaster is like a long straight cylinder with its two ends being conical and progressively growing in thickness until the cones make a full 90 degree turn. So the shape looks much like a exobar except that in most cases it is relatively longer and thinner than a exobar and both its ends make a greater turn. It is likely that the pilaster has a core, and if so, it is one of the last vortices in this part of the sequence that has one. After the pilaster and pylon the vortices do no longer have an internal core. The pilaster is a non-rotational vortex.
Two examples of pilasters are: the stem of a mushroom cloud (mesocyclic) and central bar in lenticular galaxies (macrocyclic) .
The Stem of a Mushroom Cloud
 Operation Dessert Rock, Nevada Proving Grounds. Screenshot from public domain movie by U.S. Federal Government. Image was edited with text and lines |
 Operation Buster Jangle, Nevada test site. Image by U.S. Federal Government. Image was edited with text and lines |
Mushroom clouds of large explosions are formed by revolutes. The stem of a mushroom cloud is sometimes formed by a pilaster and sometimes it is formed by a pylon. Nearly all explosions that form a mushroom cloud also form a stem, only explosions that take place higher up in the atmosphere do not show a stem. This is because the higher you go, the higher dimensional the air is and thus the state of equilibrium of the air moves from the bulb to the pylon. When the pylon becomes the state of equilibrium of the medium, then that medium can no longer show a pylon because the medium itself already behaves like one big pylon (this is explained on the page about state of equilibrium).

Most explosions only show one revolute with a pilaster or pylon as its stem. Only some explosions show both revolutes. The second revolute forms when the pilaster collides with the ground (something similar happens with the formation of a microburst). Sometimes the two revolutes are not only connected by a pilaster, but also by a cradle. The cradle is currently classified as a tunnel vortex (and discussed on the page about the tunnels), although it looks very much like a bridge as well. Two revolutes can also connect with a cradle without the formation of a pilaster, but this never happens in explosions.

Operation Upshot-Knothole, Nevada test site. Screenshot
taken from movie by U.S. Federal Government. Image
was edited with text and lines
You will never see a full cradle develop in an explosion. In most cases you will see 1/3 of a cradle, the maximum you will see is half a cradle (like in the right image above). The reason for this is that the lower revolute only partially develops or not at all. For a full cradle to form you also need two full revolutes. It is not uncommon for a tunnel vortex like a cradle to form only one half, this is observed more often with tunnel vortices. One other example is a whirlpool vortex in a bathtub, which is also half a tunnel.
Central Bar in Some Lenticular Galaxies
Some lenticular galaxies are shaped like a cradle. And some of these galaxies have a straight bar in its center. This bar is a pilaster. And while most lenticular galaxies are not cradles, those that are shaped like a cradle really are cradles. The two ends of the bar do not connect to a visible revolute, and they do not end with a conical turn. This is logical because a revolute can not appear in outer space. That is because the revolute is the equilibrium of the outer space medium. The entire outer space medium already behaves like one big revolute. And that medium is what the two ends of the pilaster connect to. The same applies to the cradle around this pilaster. The cradle ends in two sharp points instead of connecting to two revolutes.

Image by NASA, ESA, and The Hubble Heritage Team (STScI/AURA)
Image was converted to GIF anim with text, lines and green circles.
The picture above is galaxy NGC 5866, which is described by astronomers as an edge-on disc galaxy. This is a failed observation, because this galaxy does not contain a disc structure at all. The thick line at the center is a long cylinder. If we could look at this galaxy from a different angle than no larger disc structure would reveal itself behind that cylinder. Instead it would remain a cylinder.
I'm not sure what the larger, outer glow is. It could perhaps be a suprabell. But the inner vortices appear to be its nucleus.
Wake Belt
| Classification | Sixth outer bridge of the first cycle |
| Dimension | 4.75D (CW<>CCW) |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 34 (estimate) |
| States of equilibrium | Organic: Slime |
| Origin of the name | Wake because this vortex is part of the vortex wake sheet that forms behind an airplane. Belt because its total shape is like the shape of an asteroid belt or the Kuiper belt |
The vortex that connects the outer end of a left-turning scroll ring with the outer end of a right-turning scroll ring, revealing the presence of a wave with a single constant dimensionality of 4.75D, is called the wake belt. The shape of this vortex is like a very thin, flat annular ring. It is likely to be the thinnest belt that exists within the first cycle. Because this vortex connects to scroll rings, it is unlikely that it has a core. Despite being circular in shape its flow movement is not circular, the wake belt is a non-rotational vortex.
Most wake belts are invisible to the naked eye. The only known example of a visible wake belt is the vortex wake sheet that forms behind an aircraft (mesocyclic), which is only in some cases visible under the right weather conditions, of which one condition is the direction of the incoming sunlight.
Vortex Wake Sheet Behind an Aircraft

The middle section of a vortex wake sheet behind an aircraft is a wake belt vortex. The scrolls to which the wake belt connects are sometimes visible but the wake belt itself is almost never visible. The only times when it is visible is when it forms a rainbow pattern. There is an explanation on the page about the color spectrum as to why this happens. The vortex wake sheet is a type of vortex that has been studied extensively in fluid mechanics. This is not hard to imagine since it plays an important role in aviation. The wakesheet itself is not turbulence but it can cause turbulence when the wakesheet becomes unstable and falls apart (along with the scrolls). Such type of turbulence is called wake turbulence. It is for this reason that I named this type of belt the wake belt.
Since airplanes most often fly in a straight line, the vortex wakesheet most often forms in straight lines in the skies, but the full shape of a binary scroll ring is in fact a circle with a large radius. There are however characteristics about this wake sheet that reveal that it wants to behave like a circle, which was shown on the page about the spirals.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |





