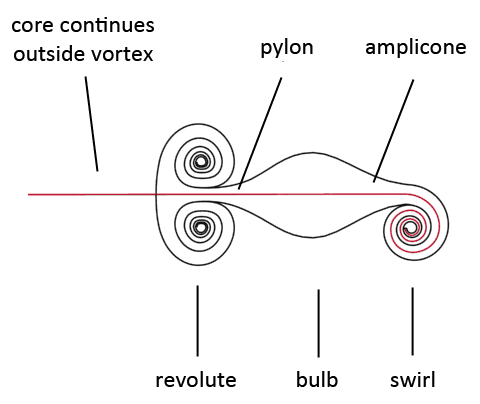
The Spirals

A spiral connects the high end of a ladder to the low end of a subsequent ladder. As an analogy, you can think about spirals as spiral staircases. As you climb the staircase, dimensionality increases. There are several variations of spirals. It is sometimes said that most spirals in nature are logarithmic, but this is likely to be false. The logarithmic spiral might be the type of spiral which we see the most in nature, but many other spiral vortices are not logarithmic. Only the swirl is a logarithmic spiral. So far, five different spirals have been found in the positive side the sequence. All of them have been observed and confirmed to exist.
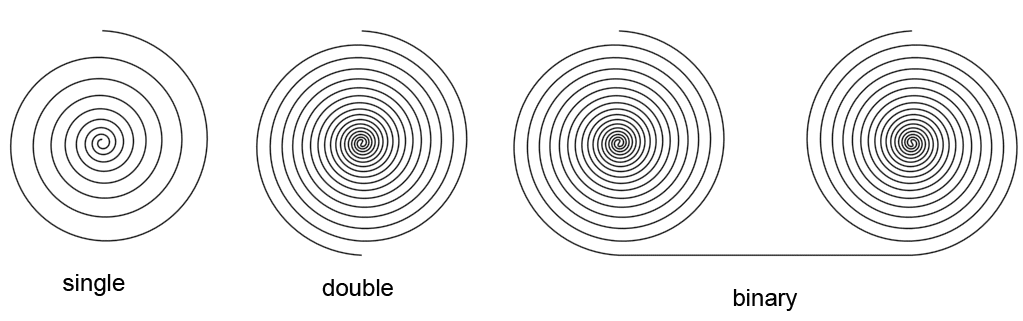
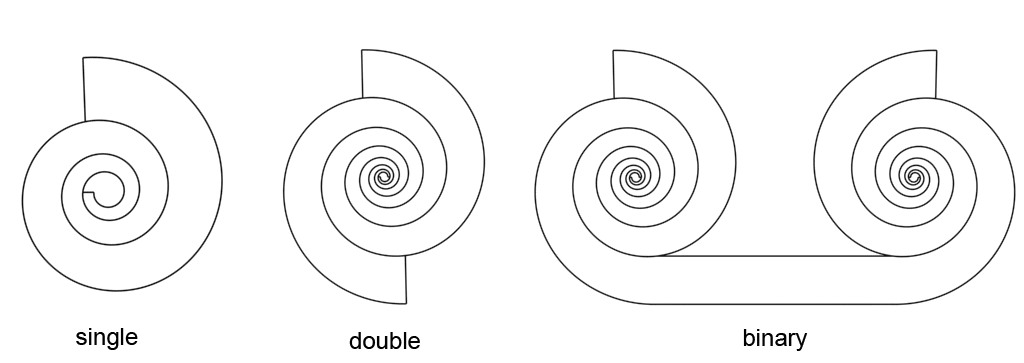
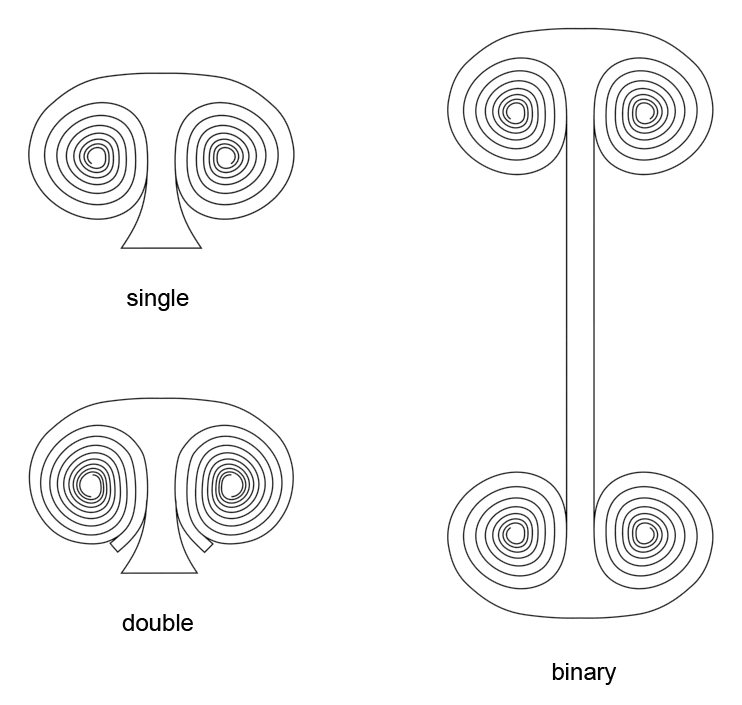
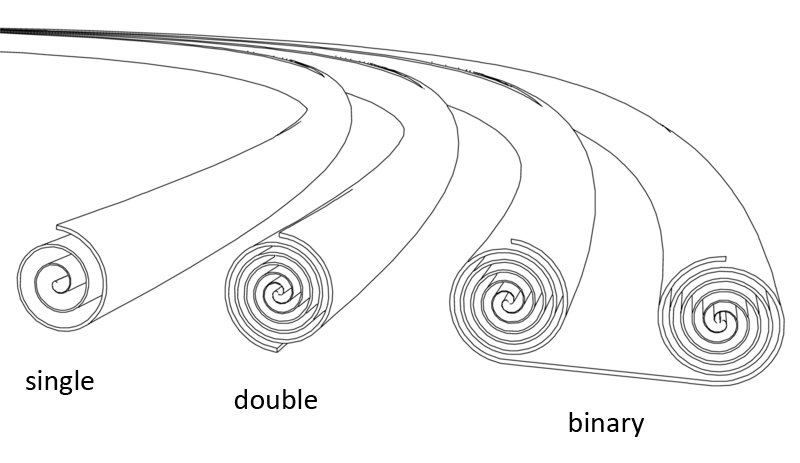
All spirals come in at least three varieties: single, double and binary. If the spiral is a binary spiral, then the vortex consists of two spirals that are mirror images of each other, one left turning, the other right-turning, and which are connected with a bridge. These bridges are also unique vortex types, but I will not discus these on this page but on the next page. The two individual spirals that make one binary spiral can be either single spirals or double spirals. Thus a binary spiral can be a single binary or a double binary. In some of the examples on this page I show a single binary, on others I show a double binary.
| Disc |
 |
| Swirl |
 |
| Bulb |
 |
| Revolute |
 |
| Scroll Ring |
 |
The last double spiral, the one that is a scroll ring, has still yet not been observed, that's why the image is replaced with the image of a puzzle piece. It is very likely that the double scroll does exist, and still is waiting to be found. The one that comes next, the binary spiral on the right, is not one that is completely certain, but likely to be a binary scroll ring.
All spirals that lie exactly on an EM crossing location or a central balance point do not look like spirals, but still very much behave like spirals. It is their characteristics, and their location in the sequence, that confirms that those vortices are spirals. On this page you will only find one spiral that lies on a central balance point, which is the central balance point of the first half-cycle, also called the main central balance point. And the vortex that lies on that central balance point is the bulb.
In most spirals that we observe in fluids the direction of the sum movement goes from the outer end to the inner end, for that it does not matter if the position of the vortex in the transformation sequence lies below or above the central balance point. For that reason, the illustrations on this page show a peripheral movement that goes from the outer end to the inner end, and a core movement that goes from the inner end to the outer end (core and periphery always run in opposite directions). But keep in mind that these directions can also be the other way around. The only condition so far that I've observed where the movement of a spiral goes from the inner end to the outer end is when a second spiral arm forms that moves in the opposite direction of the first arm. And that I've only seen in mushroom clouds that form at nuclear detonations.
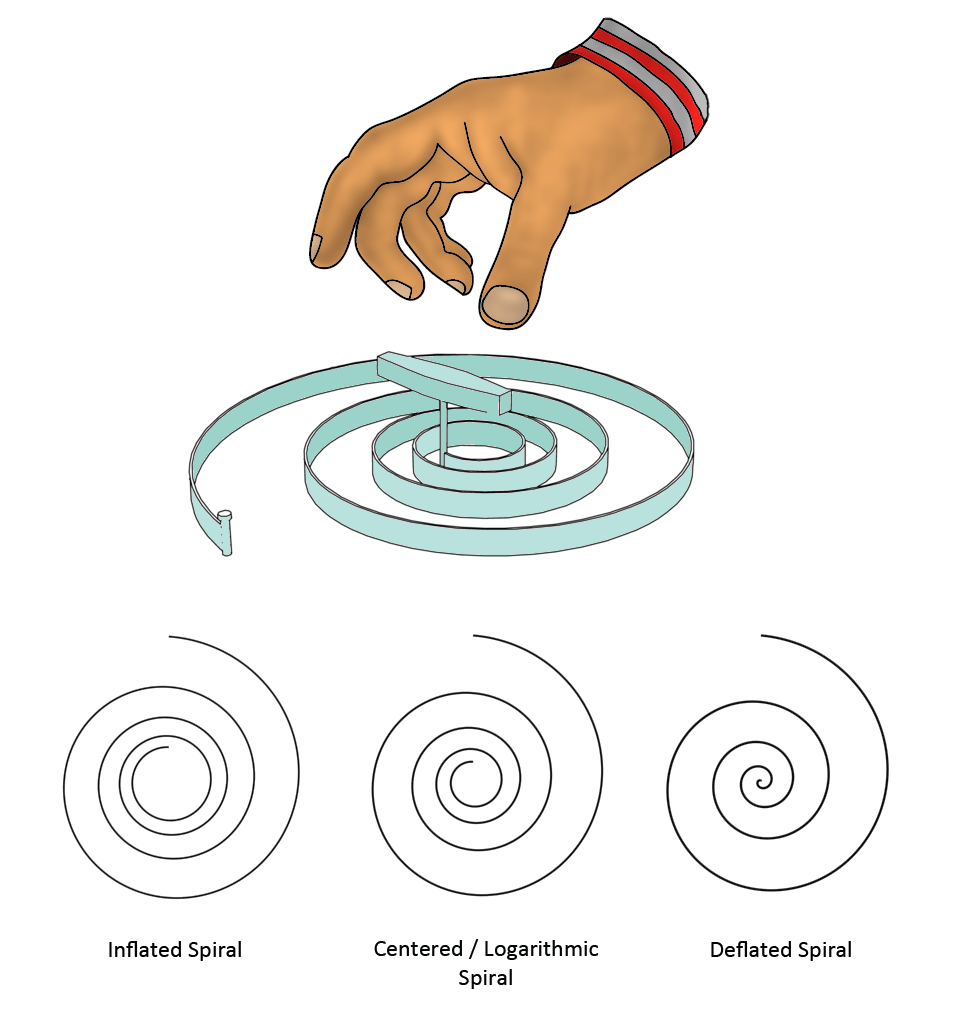
Inflated and Deflated spirals
Imagine you have a logarithmic spiral laying down on the table in front of you that is made of a single metal strip. The outer end of the spiral is fixed to the table and the inner end of the spiral is connected to a handle. Now imagine that you turn the handle of the spiral in the picture below to the right. In that case the spiral will tighten to the center and will no longer be logarithmic. In this case I call the spiral a deflated spiral. If you turn the handle in the other direction the spiral will push to the outside. In that case too the spiral will no longer be logarithmic and in that case I call the spiral an inflated spiral.
When closely examining the spirals in the sequence you will see that the swirl, when it is an unmorphed spiral, thus a vortex that has not morphed, is a logarithmic spiral. However, the disc, when it is an unmorphed spiral is an deflated spiral, and the revolute is an inflated spiral.
There are two spirals of the first half-cycle that I left out of the list, those are the scroll ring and the bulb. The bulb does not apply to these categories because it does not have any spiral arms. And the cross-section of a scroll ring appears to be an archimedean spiral, so that also does not fall into these categories.
Keep in mind that in most cases when you encounter a vortex in our physical world, then you only see a single vortex without a connection to a subsequent vortex. Only in some cases these connections are revealed to us. Examples of these connections can be found all throughout this site but will also be shown on another page later on.
Also keep in mind that binary spirals are mentioned on this page, but not much examples of them are given on this page. This is because binary spirals are connected by outer bridges, and there's a separate page that is devoted to everything about the outer bridges.
Disc
| Classification | First spiral of the first cycle |
| Dimension | 0.75D to 1.25D (second dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | No |
| Rotational sum movement | Yes |
| Minimum number of movements | 1 |
| States of equilibrium |
Inorganic: Gypsum, Some Metals Organic: Wood, Bone |
| Origin of the name | This spiral is flat and shaped like a disc. It can also be called a spiral disc but it is best to keep the name short. Do not confuse this name with 'disk', which is a different classification for a particular vortex class. |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the second positive dimension level is called a disc or a spiral disc. The disc is the first spiral in the positive side of the sequence. It connects to the helicone at the high end, and to the spire at the low end. The disc is a rotational vortex. Most discs encountered in nature come with more windings than a swirl, and their windings are more densely packed. Like any other spiral in the transformation sequence, the disc comes in three varieties: single, double and binary.
A particular feature in which disc spirals visually differ from swirls is that these discs are very flat, having almost no thickness. And the arms have no thickness as well. The disc is the low dimensional antipode of the scroll ring and the positive dimensional antipode of the sun's magnetic field. All vortices in the sequence differ in appearance depending on the medium in which they exist. But they also differ in appearance depending on size, the scale in which they appear. On the microcyclic scale, which is low dimensional (yang), the disc has very thin hard lines. On the mesocyclic scale, which is higher dimensional (more yin), the arms of the disc become wider but the disc remains flat. On the macrocyclic scale, which is more higher dimensional, the disc gradually becomes a closed disc as the seams between the spiral arms get narrower.

A disc that is completely unmorphed can not be seen with the naked eye. This is because it only consists of a core movement, no periphery. All the examples of disc spirals on this page are of partially morphed discs, only the heliospheric current sheet is an unmorphed disc. Some examples of discs in the natural world are: the center of a barred spiral galaxy and the heliospheric current sheet (macrocyclic), vortex on a wedge (mesocyclic) and the Norwegian spiral (mesocyclic), spiral growth on carborundum crystal faces (microcyclic).
Central Spiral in a Barred Spiral Galaxy

Image by HST/NASA/ESA, image was edited with a red circle
Approximately two-thirds of all spiral galaxies contain a central bar-shaped structure. In the center of the bar you will find a smaller spiral. That spiral is a disc spiral, a double disc spiral. But it is likely that there also exist binary disc spirals at the center of other barred spiral galaxies. These have not yet been found, but it is a simple and likely prediction because these binary discs have also been observed in the mesocyclic scale.
In the above picture, of spiral galaxy NGC1300, the central disc is actually not 100% a disc spiral. It is a disc spiral that has partially morphed into a swirl. The reason we know its a morphed disc is because it can be seen with the naked eye. If it would be an unmorphed disc, like the Parker spiral of the sun, then we would not be able to see it.
The Heliospheric Current Sheet
The heliospheric current sheet is the surface around our sun where the polarity of the Sun's magnetic field changes from north to south. This field extends throughout our Solar System on the Sun's equatorial plane. The spiral shape is believed to be caused by the Sun's rotation, which twists its magnetic field into an Archimedean spiral. The Parker spiral is the shape of our Sun's electromagnetic field as it extends through our solar system.
This magnetic field, which can not be seen with the naked eye, is an unmorphed disc spiral. The planets of our solar system are positioned close to the center of this disc spiral, where the central s-curve is located. The movement of these planets is not a direct result of this spiral but all of our planets do move either on or close to same plane as this spiral.

Image by NASA
The heliospheric current sheet does not look the same as a disc spiral that is very small, like the vortex on a wedge in the next example. This could be because of several reasons, none of these is sure. First reason could be because the bigger the scale, the higher dimensional a vortex is. The macrocylic scale level is much higher dimensional than the mesocyclic scale level, so this affects the basic shape of a vortex. So despite that the disc is a low dimensional vortex, it still has quite a complex shape when you encounter one on the macrocylic scale. Second reason could be that the vortex is dilated, thus the vortex is partly morphed into a vortex one cycle higher than this cycle, which could be a disk (vortex class in the third half-cycle). Third possible reason is that the polarity of the magnetic field of a disc always has this shape, and is different than the shape of the flow movement of the vortex.
Vortex on a Wedge
When fluid flows past a wedge under the right angle of direction, it forms a disc. The reason for this is that the disc is the vortex that connects to a helicone. The more an object in water is shaped like a helicone, thus a conical shape, the more likely it will spawn a spiral in the form of a disc. Thus the wedge acts like a helicone.

Image by Pullin & Perry 1980
Starting vortex on a wedge. Here, water is driven by a piston with almost constant speed to the axis of a wedge of 30 degrees semi-vertex angle. Black dye is injected into the water from small holes in the wedge surface [image and text taken from 'An album of fluid motion' by Milton van Dyke].
Norwegian Spiral
The Norwegian spiral anomaly was an event that took place in 2009. A greyish spiral of light appeared in the sky that connected to a blue glowing helix. The spiral could be seen all across the north of Norway. Unlike what the experts tried to tell you, this spiral was not caused by the trails of a rotating rocket. It was created by the rocket, but the spiral arms you see are not the trails of the jet engine. Other videos supposedly showing the same effect with other failed missile launches never show anything near of this perfect flat spiral above Norway. I do not know for sure what caused this spiral. The explanation for why this spiral appeared in the sky could be that the path of the rocket formed a helix tunnel, which is a tunnel vortex that connects to a disc spiral at its end. More about this will be explained on the page about the tunnels. What I do know is that the spiral was a single disc spiral at first and then progressed into a double disc spiral, although the second arm never grew strong.
This spiral provided me with a better understanding of how a larger mesocyclic scale disc spiral looks like. I do not know if HAARP facility EISCAT influenced the conditions of the environment so that it made it possible for this spiral to appear, but if so it was unintentional and I do not believe there was any kind of cover-up. I think it comes down to a misunderstanding resulting from scientists being forced to come up with a quick and rational explanation for something that could not be explained. In the days after the incident, tons of UFO, black-hole, secret-government-experiment and end-of-the-world theories popped up in the media. A normal and understandable response from the science community was to put an end to those extreme theories. If you don't know all you need to know to come up with a perfect answer, and you are forced to come up with a quick explanation, then the rotating rocket is the most rational explanation one could give. But it is inadequate, too easy to point at facts that contradict. The best thing to do was to say 'we don't know', yet in most cases that is not the answer that people give.
Spiral Growth on Carborundum Crystal Faces
Microscopic spirals sometimes appear on the surfaces of solids grown slowly from solution. The picture below shows spiral growth on carborundum crystal faces. There are proposed theories as to why these spirals grow on these surfaces, but none of them are certain. The shape of this spiral does look most like the shape of a disc spiral. That it appears on the surface of crystals would be a logical consequence of the state of equilibrium of the medium. The state of equilibrium for crystals is the spire, which is the vortex that is very close in the sequence to the disc. Thus for that reason a disc is likely to appear within crystal, more likely than a higher dimensional vortex.

Crystallographic Laboratory, Geological Institute,
University of Ghent
Swirl

| Classification | Second spiral of the first cycle |
| Dimension | 1.75D to 2.25D (fourth dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | 1 + 2 |
| States of equilibrium |
Inorganic: Water Organic: Unknown |
| Origin of the name | It is named swirl because of its spiral shape movement |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the fourth positive dimension level is called a swirl. The swirl is a rotational vortex which is the second spiral in the transformation sequence. It connects to the amplicone at the high end, and to the helicone at the low end. Its shape is the classic logarithmic spiral which we often see in nature. Unlike the disc, which is nearly flat, this spiral has arms whose thickness grows at a linear rate. It's appearance is that of a rolled up cone. The thickness of the swirl depends on the medium in which it exists. The swirl is thicker in high viscosity fluids. Like any other spiral in the transformation sequence, the swirl comes in three varieties: single, double and binary.
You need at least 3 movements to make a swirl. There's a core through the center of the vortex and two opposing peripheral movements (meridians) rotating around the core in opposite direction. The swirl contains fewer windings than the disc. The swirl is the low dimensional antipode of the revolute. Some examples of swirls are: spiral galaxies (macrocyclic), hurricanes (mesocyclic) and swirling vortex behind an airplane (mesocyclic).
Spiral Galaxy

Image by European Space Agency & NASA, (ESA/Hubble)
All spiral galaxies are swirls. Nearly all of them appear to be double spirals. Because these galaxies lie in the outer space medium, which is high dimensional (yin), they are also quite thin when we look at them edge-on. This is because those swirls are diffused. The spiral arms split into multiple spiral arms as they extent outward from the center of the spiral. These swirls are less thick than swirls found in denser mediums, but they have substantial thickness nonetheless.
A spiral can flow, or a spiral can rotate. Both movements are substantially different. When a spiral flows, the spiral arms do not move, instead the movement flows in the direction of the spiral arms. When a spiral rotates, the spiral arms do move, and the entire spiral rotates around the center of the core. The movement that these galaxies make might be a combination of these two movements. This is because of the likely comparison of spiral galaxies with hurricanes. Satellite views of hurricanes show spirals that appear to both flow and rotate. I say 'appear', because I'm not completely certain of this. A flow movement does look somewhat like a rotational movement and be mistaken for one.
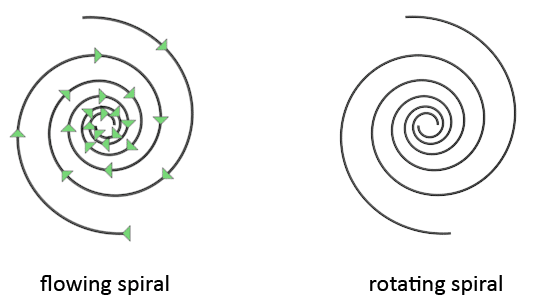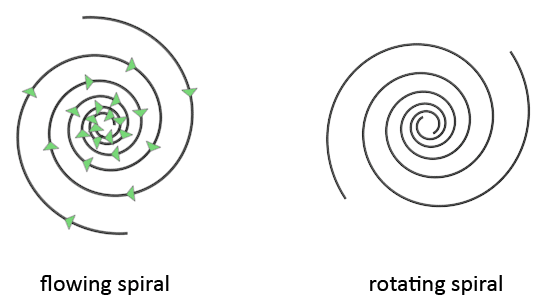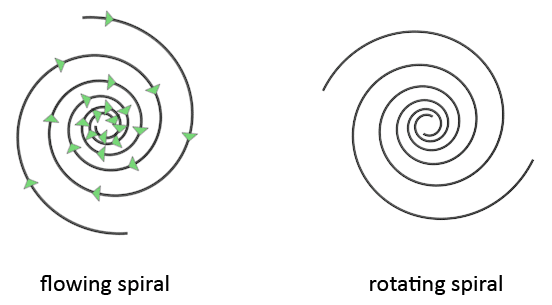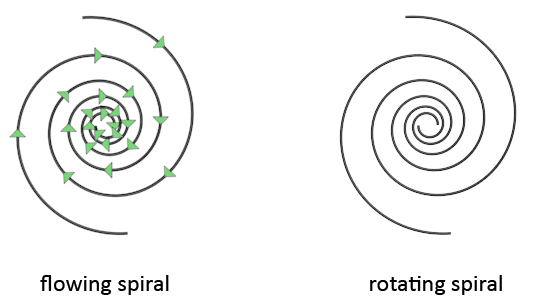
The consequence of the flow movement of the galaxy is that stars continuously disappear at the center of the galaxy, and new stars continuously form at the other edge of the galaxy, at the start of the spiral arms. The comparison with hurricanes might not be completely valid, because of the difference of what is located at the center of the spiral. Spiral galaxies have spiral bars and a central disc spiral. Hurricanes do not. It might be that these inner vortices also influence how the spiral as a whole rotates, or not rotates. The answer to this can not be given at this moment because there are no observations of swirl spirals here on earth with a spiral bar and disc at the center. Only in space so far we observe these vortices, and unfortunately, we can only see their static image. We can not see these galaxies move.
A spiral that is connected to a tunnel vortex does not rotate. And that might be a consequence of what's located at the center of the spiral.
Hurricane
 Image by Nasa |
 Image by U.S. National Oceanic and Atmospheric Administration |
Hurricanes in our atmosphere are what spiral galaxies are in space. We can learn from any of them by looking at the other. We cannot see how spiral galaxies move. Telescopes provide us mostly with static images of outer space. Spiral galaxies move way too slow to be able to study their movement. But we can understand a lot about their movement by looking at hurricanes.
The movement of a hurricane is not caused by gravity. Nor is the movement of a swirling vortex behind an airplane caused by gravity. The orientation of the hurricane is influenced by gravity. And the direction of rotation depends on what hemisphere of the earth the hurricane is located on. But the force that creates these hurricanes is not gravity, instead it are the weather conditions on earth that form these hurricanes. So too do similar space weather conditions cause a spiral galaxy to form and creates a movement that pushes the stars along with the flow of the vortex.
Swirling Vortex Behind an Airplane

Image by Langley Research Center of the United States
National Aeronautics and Space Administration (NASA)
The air flow from the wing of this agricultural plane is made visible by a technique that uses colored smoke rising from the ground. The swirl at the wingtip traces the aircraft's wake vortex, which exerts a powerful influence on the flow field behind the plane. Because of wake vortex, the Federal Aviation Administration (FAA) requires aircraft to maintain set distances behind each other when they land [text from Wikipedia].
We see only one vortex in this image, but there are actually three vortex types present behind the wing of the airplane. These three vortices are a consequence of one another. The first vortex is the wingtip vortex which extends from the tip of the wing. That vortex is a spire. Around the vortex a scroll spiral forms, the spire becomes the center axis vortex of the scroll. And then when that scroll comes in contact with the colored smoke, a swirl spiral forms at the cross-section of the scroll.
The scroll is not visible because it is too high dimensional. The spire is not visible probably because it is unmorphed. A spire that is unmorphed is not visible, but if the spire is unmorphed then it does not have a periphery, a vortex without a periphery can not push matter around, it is only electromagnetic. A spire that is upmorphed does have a periphery and should be visible.
Bulb

| Classification | Third spiral of the first cycle |
| Dimension | 2.75D to 3.25D (sixth dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 1 + 7 (estimate) |
| States of equilibrium |
Inorganic: Air Organic: Unknown |
| Origin of the name | It is named bulb because of its bulbous shape |
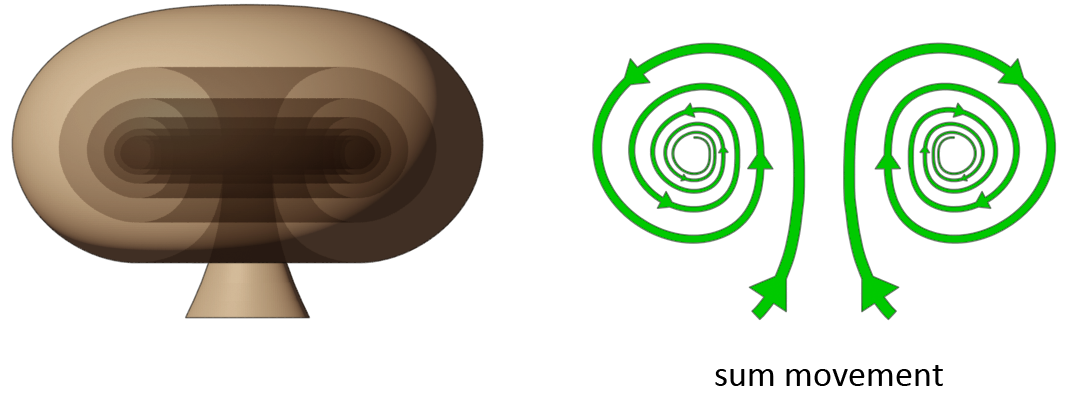
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the fifth dimension level is called a bulb. The bulb is the third spiral in the transformation sequence. It connects to the pylon at the high end, and to the amplicone at the low end. The center of the bulb lies exactly on the central balance point, thus at 3.0D. Anything above the bulb is high dimensional (yin), anything below the bulb is low dimensional (yang). Because the bulb lies on the central balance point it has no high dimensional or low dimensional antipode.
Because the bulb lies on the central balance point, the sum of contraction and expansion is zero, thus in stasis. The consequence of this is that the vortex has a bulbous shape without visible spiral arms, and therefore it is a non-rotational vortex despite being a spiral-type vortex. Below you see an image of how the bulb connects to its upper and lower ladder, which is the pylon and the amplicone.
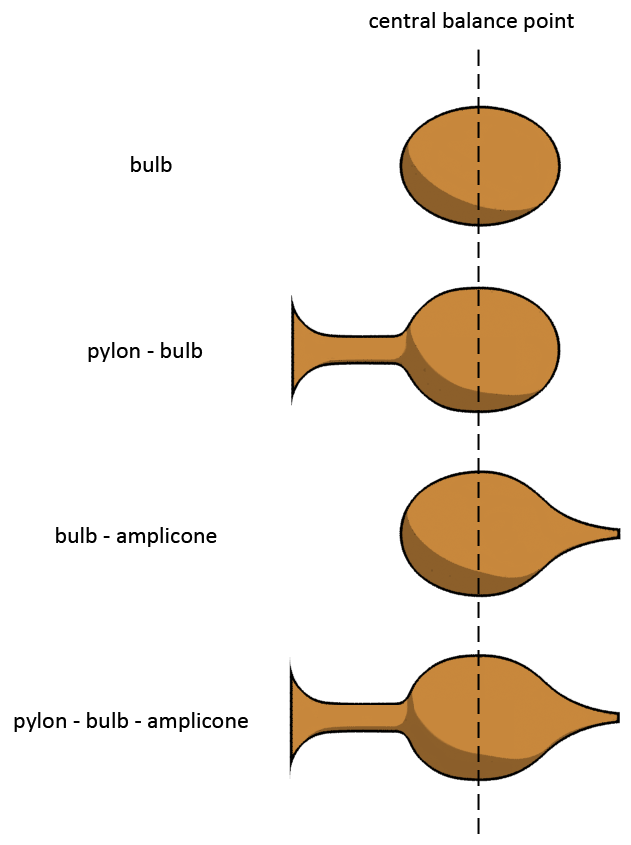
The bulb is the odd one out of all the spirals on the positive side of the sequence, this is because unlike all other positive dimensional spirals, this spiral-vortex does not have visible spiral arms. For this it took me a long time to figure out that this vortex is actually a spiral. It is a spiral because of its location in the morph sequence and because it behaves exactly like a spiral in several different ways. For a long time I believed that the pylon, bulb and amplicone were one and the same vortex, one big ladder. But then I got stuck when I tried to solve the entire puzzle of the morph sequence which did not fit with the logic in that way. Only when I understood that the bulb was a spiral and not part of a ladder I was able to complete the puzzle. It only takes a little bit of thinking to come up with a possible reason as to why the bulb does not have any spiral arms. The previous spiral, at the low side of the sequence, is the swirl. The swirl has spiral arms that rotate inward (when coming from the direction of the bulb), making a contractive movement. The spiral that comes after the bulb, at the high side of the sequence, is the revolute. The revolute has spiral arms that rotate inward (again when coming from the direction of the bulb), but this inward flow rotation is an expansive movement. It looks like they rotate inward but you need to analyze the situation carefully, and especially look at how the movement starts. The vortex makes an expansive movement, not contractive. In between these two spirals is the bulb (separated by two ladders), which lies exactly on the central balance point. So logic tells us that its spiral arms should not rotate inward nor outward, because its position determines that the tendency of the arms to rotate either inward or outward is precisely balanced.

THE BULB IS A SPIRAL WHOSE SPIRAL ARMS ARE IN STASIS, NOT ROTATING INWARD OR OUTWARD, BECAUSE OF THE VORTEX LOCATION ON THE CENTRAL BALANCE POINT
Another consequence of this is that both the inner end and outer end of the spiral lie on the same distance from the center. All these unique characteristics are a consequence to the fact that the bulb lies exactly on the central balance point, which is why its appearance is different from the other spirals.
Some bulbs that we observe in fluids are stretched out along their directional axis, others are flattened, and some are almost perfectly spherical. These different proportions are the result of the vortex being stretched and deformed by external forces, like environmental pressure or gravity. When those vortices are removed the bulb takes on its basic shape.
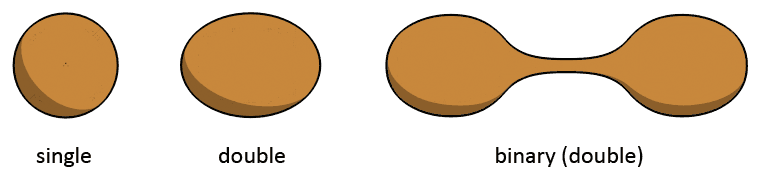
Just like with any other spiral, this one too comes in three varieties. Here too it was quite hard to find the right puzzle pieces. The single nor the double version does not look like a spiral. There are two versions, a round bulb and an ellipsoidal bulb. One is the equivalent of a spiral with one arm, the other is the equivalent of a spiral with two arms. There is no hard line between a single spiral and a double spiral. A spiral can be something in between a single and a double when one of the two spiral arms has not fully formed and thus is shorter than the other arm. So too can a bulb be something between a single bulb and a double bulb by appearing in a shape that looks like something in between.
A spiral can also be a morphology between a swirl and a bulb. The drawing below shows how a lowmorph bulb looks like, thus a bulb that is partly morphed into a swirl. Why it has this shape will be shown later on.

Some examples of bulbs are: Elliptical galaxies (macrocyclic), vortex in rotating flow through a tube (mesocyclic) and water droplets (mesocyclic).
Elliptical Galaxies

Image by NASA
There are two types of elliptical galaxies, one of them are bulbs and the other are vessels (a bell vortex). And it is not always easy to determine which one is which. If you see an elliptical galaxy that is soft, with no hard edges, and that gets progressively brighter towards the center, then that elliptical galaxy is a bulb. If you see one that is very bright, with hard edges and the same white color all the way from its edge to the center then those elliptical galaxies are vessels. Above is an image of giant elliptical ESO 325-G004 which lies in the cluster of galaxies Abell S0740. This galaxy is shaped by a bulb vortex. Vessels are discussed on the page about the bells.

This is sort of like the same idea when you work with Photoshop and you can select a soft or hard brush. A soft brush is a bulb, a hard brush is a vessel. What we cannot see in these photos is that the hard elliptical galaxies are hollow, and the soft ellipticals are not. There is no, or relatively little star formation, or a different kind of star formation inside a vessel elliptical galaxy as compared to its outer shell.
Besides these two different types of elliptical galaxies, one hollow and the other non-hollow, an elliptical galaxy can also be an almost perfect sphere, instead of an ellipsoid. The first one is an equivalent of a spiral with one arm, the second is the equivalent of a spiral with two arms. Some elliptical galaxies appear to be spherical, the only problem is that this can also be the consequence of its orientation in the direction that the photo was taken. In most cases one can not be sure if the elliptical galaxy is a spherical galaxy.
Interacting Galaxies
A swirl that connects to a bulb is something that you will not find in fluids, at least not in air or in water. The reason for this is that the swirl is the state of equilibrium for water, thus a swirl can not be seen in water. And the bulb is the state of equilibrium of air, so a bulb can not be seen in air. So a full swirl-bulb connection can not be seen in those two media. That is why I haven't found any other examples here on earth of this vortex pair. The good thing is that we can look in outer space to find this vortex connection.
|
ARP94
|
AM1316-241
|
Messier 51

Image by NASA & ESA
Above are three images of interacting galaxies. They are called interacting galaxies because it is believed that these spiral galaxies and elliptic galaxies are colliding. That these two galaxies are seen so close together is thus believed to be pure coincidence, thus as chaos, not because of any logical pattern. But even when you don't know anything about the transformation sequence, and you look at these three images then one detail that do not fit with the word chaos. And that is that in all these three images, the elliptic galaxy lies in the same plane as the spiral galaxy. The reason for that is that these three images are images of a swirl-bulb connection, thus a logical follow-up in the sequence, these are not galaxy pairs that are formed by random chance.
But one thing that is inconsistent with this theory is that there is no amplicone in between the swirl and the bulb. There are no known observations of an unmorphed amplicone in outer space. It could be that that type of ladder vortex can not be visible in outer space. It still could be that the amplicone is present in both ARP94 and AM1316-241, but that it can not be seen. Still, the location of the bulb and its distance to the swirl suggests that the amplicone is there, in between the two vortices.
I am not completely convinced that Messier 51 actually shows a swirl - bulb connection. It could be that we are looking at a binary spiral. The last part of the spiral arm that connects to the bulb could be a troth, thus an outer bridge vortex. I do not expect that to be so because then I would expect both spirals to be bulbs or both spirals to be swirls, but it could be that in some cases a bridge can connect two different spiral types in the case that only one of the two spirals morphs upwards. We need to find more examples to be sure.
Vortex in a Rotating Flow through a Tube
The bulb is one type of vortex that has already been studied in fluid mechanics. Only it does not have an official name, only here on this site its called a bulb. It is important not to mistake a bubble with a bulb and vise versa. A bubble is hollow, filled with a gaseous substance, a bulb is not hollow but it's density is different from the water around it. Here it is easy to determine that this vortex is a bulb because it also shows its subsequent vortices, the pylon and the amplicone, at either side. In this example the revolute hasn't formed, but there are more examples later on that show this same kind of setup with a fully formed revolute.

Water to which rotation [text edited to avoid confusion due to conflict of terms] has been imparted by vanes upstream flows through a slightly diverging tube. Dye is injected upstream. A smooth, almost axisymmetric body of fluid is formed. Sarpkaya 1971. [Text and image taken from 'An album of fluid motion' by Milton van Dyke. Image was edited with text and arrows].
The video below shows a similar type of example, but this time the revolute does have formed. This vortex actually shows four different subsequent vortices in the sequence being connected to each other simultaneously. Two of which are ladders, and two are spirals. These are the amplicone, the bulb, the pylon and the revolute.
 |
Water Droplets
Unlike the vortex in a rotating flow through a tube, which was discussed previously, one can not tell at first glance that a water droplet is a bulb. This is because a water droplet, when at rest, does not show the connections to its subsequent vortices, the pylon and the amplicone. But it are these two ladder vortices that here as well reveal that droplets are bulbs, because they do form when you start to play around with them. A water droplet that drips down from a sharp tip forms an amplicone as a tail. A water droplet that drips from a blunt solid forms a pylon (right image).
 |
 |
Interestingly, to make the photo on the left, I had to place the water droplet on a leaf. I wasn't able to form a water droplet on a metal, wood, or stone surface, because the surface tension would not hold and the droplets instantly fell apart.
The movement of the bulb can be seen at its best in this slow motion video here below. Not all of the movement of the water seen in this video is movement of the bulb. Some of it is movement of the pylon, some is movement of the exobar, and other is higher dimensional movement.
Video by the Slow Mo Guys
Droplets of quicksilver are also bulbs. Some, but not all liquids can form bulbs as droplets when surrounded by air.
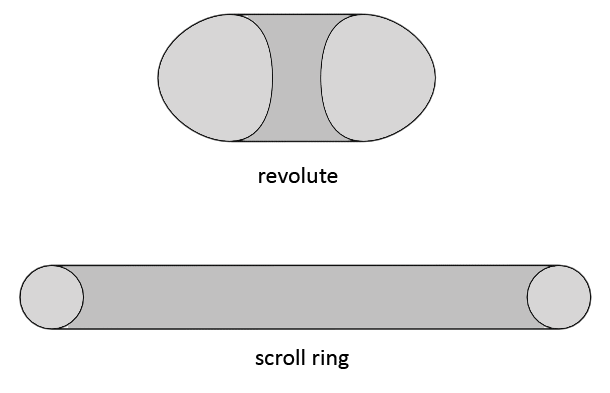
Revolute
| Classification | Fourth spiral of the first cycle |
| Dimension | 3.75D to 4.25D (eighth dimension level) |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | 21 (estimate) |
| States of equilibrium |
Inorganic: The outer space medium (at macrocyclic scale) Organic: Gelatin |
| Origin of the name | Revolute means 'curved' or 'curved back'. It also refers to the word 'revolving' |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the eighth dimension level is called a revolute. It is the third spiral in the positive side of the transformation sequence and one of the more complex. The revolute is a rotational spiral vortex. Its shape can be determined by studying smoke rings in the first few seconds when they form. The revolute connects to the aureole belt at the high end, and to the pylon at the low end. Like any other spiral in the transformation sequence, the revolute comes in three varieties: single, double and binary. The picture below shows these three varieties. Note that in the picture above I also added the pylon. The pylon is not part of the revolute but I added it because without it its a bit harder to see what you're looking at. The same I did in the illustration below (left two images)
The revolute is the first vortex in the sequence that produces ultrasound (when the medium in which it exists is air). The revolute is also the first vortex in the sequence that does not have a core. The pylon is the last vortex with a core. After the pylon, the core proceeds in a straight line. Presumably this core runs all the way to infinity. The red line in the picture below is the core.
The cross-section of the donut shape is not spherical, although it does appear to be spherical if you don't look carefully. When examining a revolute vortex closely one can find out that its section is flatter on one side than it is on the other. When a revolute morphs into a scroll ring this non-uniform shape disappears and its cross-section become more and more round. A large thin torus has sections which look completely round.
The revolute is a standard inflated spiral. It spirals progressively slower in proportion to its turning radius as it spirals inward to the center. So the more it spirals to the center, the less it looks like it will ever touch the center. This is why there must be other vortices after the revolute that cross the gab towards the infinity ring.
I call it a revolute because of the way that the movement of the revolute starts from the low end of the vortex. I also chose to use a unique new name instead of using the name 'vortex ring', because in fluid mechanics, both a revolute and a scroll ring are called a vortex ring. Until now no one knew that these were two different vortex types.
Some examples of revolutes are: large explosions (mesocyclic), volcanic eruptions (mesocyclic), smoke and water rings at their early stage (mesocyclic), reaction diffusion system (microcyclic).
There are no examples of revolutes in the macrocyclic scale level because the revolute is the equilibrium of the outer space medium, thus the outer space medium behaves like one big revolute, but no revolute can appear in the outer space medium. This is something you will read about on the page about the state of equilibrium.
Large Explosion
 Image by U.S. military or Department of Defense |
 Image by Jon Sullivan |
Large, intense explosions in air often form revolutes. Some small explosions sometimes also do. We are all familiar with the well-known mushroom cloud shape that we see with nuclear detonations. But at first glance, we would not expect these giant mushrooms to be anything like a spiral. Yet these mushrooms are spirals. If we would be able to see how the movement progresses inside the vortex, then we would known that the movement is like a spiral, a complex spiral.
Volcanic Eruption
_UnderCCBY3.0.jpg)
Image by Paginario (Wikimedia), under CC BY 3.0 license
Volcanoes produce, just like explosions, large mushroom clouds. These mushroom clouds are revolutes. This is pretty much the same as with explosions. Except the difference here is that in some of these volcanic eruptions the mushroom cloud is lower dimensional then with explosions, this occurs when there's a large amount of heavy debris within the cloud. In that case mushroom cloud is a lowmorph revolute. Thus a revolute that is partially morphed into a bulb.
Smoke and Water Rings at their Early Stage
Smoke and water rings have been studied in fluid mechanics. In the last couple of decades our understanding about the structure of these vortices has grown significantly. Below are two images that show the inner structure of the vortex. One in air, and one in water. Notice that in air the revolute has more windings, spiraling in smaller steps to the center. In water, the revolute has less windings, spiraling in larger steps to the center.
When you first look at a mushroom cloud or a vortex ring in water, you don't see that its a spiral because the windings are hidden inside. It are images like this that reveal the spiral shape to us. It is a spiral, but not flat like we are used to in common mathematical spirals. This one is circular, because it is more complex, higher dimensional.
 Image by T. T. Lim |
 Image by Ali Olcay and Paul S. Krueger, National Science Foundation |
left - Structure of a smoke ring. Photograph taken by T. T. Lim.
right - Vortex ring formed by sudden ejection of fluid from a tube. During ejection, the jet rolls up into a toroidal spiral (ring) and in the process, entrains some of the ambient fluid into the spiral. This process is easily visualized by dying the fluid in the tube with a fluorescent dye and illuminating it with a laser sheet (known as planar laser induced fluorescence or PLIF) to obtain a cross-section of the flow as shown in the image. source: http://lyle.smu.edu/~pkrueger/vrentrainment.htm
From these images we can see that the revolute is not a logarithmic spiral. The distance between the windings does get smaller as the spiral arms progress to the center, but the more the arms rotate to the center the less it appears to be reaching that center. Eventually it clearly wants to form a donut shape, it does not want to reach the central ring. However, other vortices can take over at those deeper winding locations and bring the movement closer to the infinity ring, eventually it is the last ladder that can reach the central ring.
Note that not all smoke and water rings are spirals, some smoke rings and most water rings (called bubble rings) are bell vortices, those vortices do not have the windings of spiral arms. You will read more about those vortices on a page further ahead.
Ink Dropped into Water
This video shows a revolute being formed by ink being dropped into water. You can clearly see the inner windings being formed in this video.
Reaction Diffusion System
The picture below I found by browsing the web. It is the three dimensional computer simulation of a reaction diffusion system. I do not know what a reaction diffusion system is and you might be someone who does not know either. But its shape suggests that we are looking at a revolute. Notice that the word 'scroll' in the text does not imply a vortex type. The word just happens to conflict with the terminology introduced on this site.

Image by Arthur Winfree
Winfree and Strogatz (1984) have studied the 3 dimensional behavior of reaction diffusion systems. They find that reaction diffusion waves commonly appear as involute spirals or scrolls radiating from tiny rotating activity patterns called "organizing centers." The scrolls emanate from their central organizing axis which typically forms a closed ring or toroidal vortex. The origin of the waves is defined as a phase singularity whose immediate neighborhood is a rotating pattern of chemical activities, the pivot of the rotating spiral wave from which it radiates. The ostensibly flat spiral is actually a cross section of a three dimensional wave shaped like a scroll which emerges from a filament of singularity in 3 dimensions [image and text from Ultimate Computing: Biomolecular Consciousness and NanoTechnology By S.R. Hameroff].
Scroll Ring
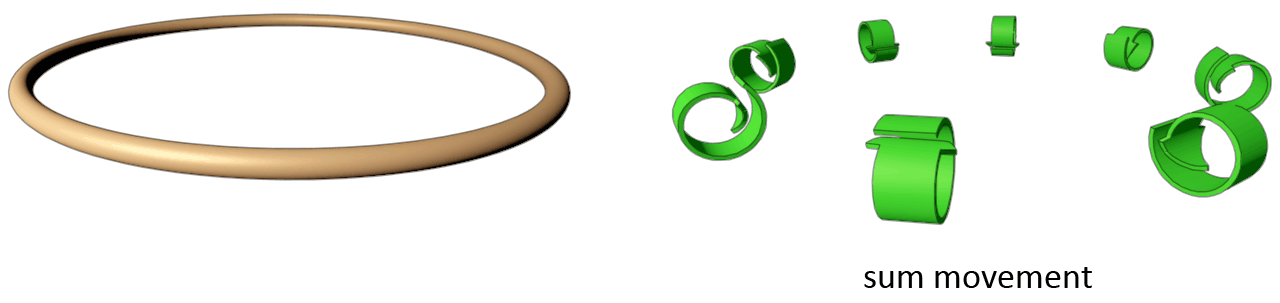
| Classification | Fifth ladder of the first cycle |
| Dimension | 4.75D to 5.25D (tenth dimension level) |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | 55 (estimate) |
| States of equilibrium |
Inorganic: Unknown Organic: Saturated Fat |
| Origin of the name | Its inner windings are shaped like a scroll. The total shape is that of a ring |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the tenth positive dimension level is called a scroll ring, or simply 'scroll'. Its shape resembles something like a thin circular scroll. The scroll ring is the fifth and last spiral in the positive side of the sequence. It connects to the aureole belt at the low end and to the omega ladder at the high end. As is the case with most other spiral-type vortices, the scroll ring is a rotational vortex. It is not known whether it is a standard inflated or a deflated spiral. The cross-section of the vortex might be something close to an Archimedean spiral.
The most common name for this vortex is scroll ring. But because this vortex most often does not appear in a full circular form, I will in those cases simply use the word 'scroll'. This is one of the characteristics in which this vortex differs from a revolute vortex. A revolute can only appear in a full ring form, while the scroll can appear as only a section of a ring. And it is not always circular but can bend in all directions. This might perhaps be possible because of the many peripheral movements (meridians) that a scroll ring has.
So whenever a scroll is a full ring, I use the name 'scroll ring'. Whenever the vortex is not a full ring, I use the shorter name 'scroll'. It is still the same type, with the same characteristics.
We can observe this same characteristic in other vortices that are higher dimensional than a revolute and circular in shape. One such vortex is the wake belt. It is likely that the laminar belt, aureole belt, omega bridge and are all vortices that share this same characteristic. They can all appear as either a straight or deformed section of a circle and not per see in a full circle form. This can make it harder to identify the correct vortex type. You always need to look for the right clues to be able to determine whether a scroll ring or wake belt really is a scroll ring or wake belt when it does not appear in circular form.
Above you can see an image of the three varieties of the scroll ring, single, double and binary. Below is a cut-through model image that shows how the scroll ring is positioned deep within the revolute when connected in a sequence. The image shows how these vortices look in the transformation sequence, but this part of the sequence hasn't been observed yet. People who study fluid mechanics have never seen a setup like this deep within a vortex ring. But if you've read all the pages until here, then you must already be starting to understand the logic as to why a setup like this is to be expected. You've seen all the other of the 4 turns, 5 ladders and 4 spirals on the positive side of the sequence, and what you see in the image below is the logical continuation of the sequence.
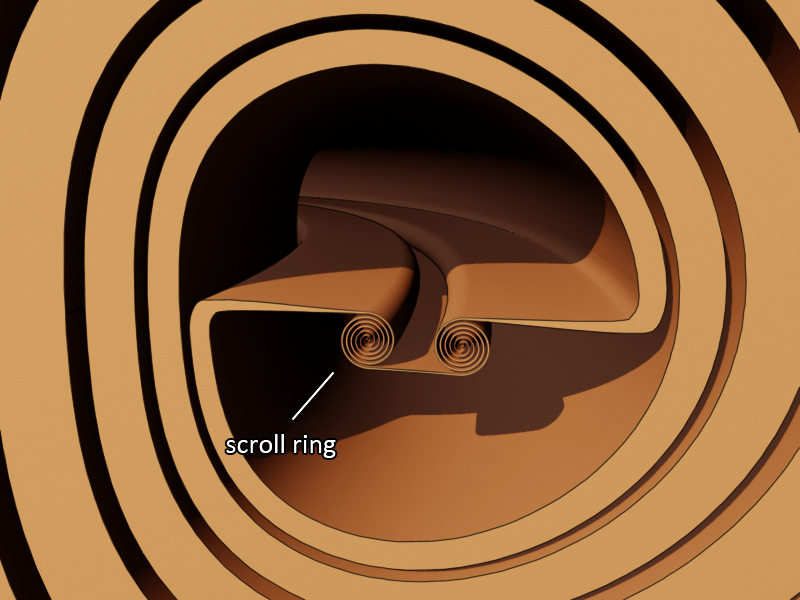
A possible reason that we don't see these vortices all together in explosions and vortex rings (at their early stage) is that one arm of the spiral makes an inward movement and the other arm of the spiral (if it forms) makes an outward movement. I think that for the belt to form within a revolute both spiral arms must make an inward movement. Otherwise an inner bridge will form instead of two opposing ladders. So it could be that in spiral galaxies, both spiral arms move inward, and thus a spiral bar in the form of two opposing ladders can form inside the swirl, which is almost similar in how the vortices form inside a revolute. It is unknown at this point how such a movement and thus a vortex like in the image above can be produced in experiments here on earth. We can however produce all the vortices in the picture separated from each other, but not all connected like in the picture above.
Some examples of scroll rings in nature are: horseshoe vortices (mesocyclic), contrails in a vortex wake sheet (mesocyclic) and plunging breaking waves (mesocyclic).
Horseshoe Vortices
Below is a photo showing three horseshoe vortices. These horseshoe vortices are scroll rings that have not formed a complete circle. There are two reasons why I show this example. The first reason is that this example is the closest one we have so far that shows how the scroll ring connects to a belt. The flow of the smoke is flat / planar, just like the movement of the belt. But the flow of the smoke is in one direction, while the movement of the belt should be circular. That is the reason that these scrolls do not form full circles. In this setup, the flow comes from a single direction. For a complete scroll ring to form the flow must be circular coming from all sides simultaneously. The two outer rings could perhaps be a binary scroll ring. But it is hard to see how they are connected so it cannot be confirmed if that is so.

A horseshoe vortex system is visualized with smoke in the cross-flow laminar boundary layer, whose displacement thickness is approximately 0.1 in. The jet, at the left side of the photograph, issues directly at the viewer. Three horseshoe vortices are seen to wrap around the jet. Such a horseshoe vortex system is somewhat similar to what is observed in the near wall flow around a wall-mounted circular cylinder. Picture taken from 'A Gallery of Fluid Motion', Cambridge University Press.
This also confirms that the belt vortices inside the revolute are those vortices that are responsible for the occurrence of laminar flow in fluids. Laminar flow occurs when a fluid flows in parallel layers, with no disruption between the layers. This is not that surprising since the shape and movement of laminar belt strongly suggest that laminar flow is induced by those vortices. The laminar belt is named after this phenomenon, because it is the vortex that is most likely to be the one responsible for most of the laminar flows that occur in fluids.
LAMINAR FLOW = MOVEMENT INDUCED BY THE LAMINAR BELT
I do must add here that the type of laminar flow that is linked to movement of the laminar belt is a non-rotational type of laminar flow. When the laminar flow is a rotational flow then that movement is caused by some other type of vortex movement, which is not the laminar belt.
The second reason I show these horseshoe vortices is seen in this video below. Here is another example of a scroll ring using a setup that is somewhat like the one used in the previous photo. Again, not a full one. This one is formed by hydrogen. This video shows the inner windings of a scroll. It was this video that made me suspect that the cross-section of a scroll ring is close to that of an Archimedean spiral. I'm not sure because it is hard to tell, but this video shows that studying these horseshoe vortices could lead to important answers.
movie © ONERA, converted
from Quicktime
Contrails in a Vortex Wake sheet

Contrails are artificial clouds that are the visible trails of condensed water vapor made by the exhaust of aircraft engines. As the hot exhaust gases cool in the surrounding air they may precipitate a cloud of microscopic water droplets. I have to be a bit careful here in saying that contrails are scrolls, because that is not entirely right. The trails that come out of the engines are not scrolls. There is an invisible vortex behind the airplane called the vortex wake sheet, this vortex is a binary scroll that is stretched out in a straight line. When the trails made by the engine's exhaust come in contact with this wake sheet, they take the shape of the wake sheet, thus revealing the vortex that is otherwise invisible. If you look at the photo above, you can see 4 engine trails directly behind the aircraft, but further to the back they become two large trails because they take the shape of the vortex wake sheet.
This vortex wake sheet consists of two scrolls that are connected with a bridge. The trails made by aircrafts are mostly stretched out in a straight line. But we know that the scroll ring is a circular vortex. A consequence of this can be seen in the image below. The picture shows a vortex trail of an aircraft. The trail deforms, breaks open then forms a series of rings. This is called the Crow instability. The reason that this happens is that the scroll ring is stretched out in a straight line, which is an undesired state for this type of vortex. A scroll ring wants to be circular. That is why the trailing vortices break up and form rings.

Instability of a pair of trailing vortices. The vortex trail of a B-47 aircraft was photographed directly overhead at intervals of 15 sec after its passage. The vortex cores are made visible by condensation of moisture. They slowly recede and draw together in a symmetrical nearly sinusoidal pattern until they connect to form a train of vortex rings. The wake then quickly disintegrates. This is commonly called Crow instability after the researcher who explained its early stages analytically. Crow 1970, image by Meteorology Research Inc. [Image and text from 'An Album of Fluid Motion' by Milton van Dyke].
The name 'crow instability' is a misleading term. It suggest that the vortex becomes unstable and falls apart. But it is actually the other way around. The vortex was unstable at start, because it existed in a undesired state, an undesired shape. Then when it fell apart and formed these rings it entered a more stable state, in which the vortex wants to exist.
This next video shows a good demonstration of the crow instability.
Spiral Formation in Cigarette Smoke
_UnderCC0.jpg)
Image from Geofreund (Pixabay)
Not all types of smoke are similar when it comes to vortex movement. Smoke from a burning cigarette is higher dimensional than smoke from burning wood, you can see this by looking at the patterns that emerge within the smoke. Cigarette smoke tends to create patterns that are more visually appealing, making it a good source for spectacular professional photography. The scroll ring is one vortex that occurs quite often in cigarette smoke, although it most often does not form full rings but does show well defined scrolls. The photo above shows one such example of a scroll spiral in cigarette smoke.
Plunging Breaking Waves

Footage taken from & Again, by Blake Vincent Kueny
& John John Florence
Plunging breaking waves generally appear at the coast lines, where the water depth is shallow. As the wave progressed towards the coast line, the water depth lessens, and underneath the wave a force builds up in the opposite direction of the traveling wave. This enables the wave to overturn itself at its highest point.
The rolling water vortex that is created by this motion is not a scroll ring, but only a scroll. It is only a section of a ring. And the scroll itself does not make more than one flow rotation, it forms only the first flow rotation of a spiral arm. Because of the force of gravity, it is not possible for an ocean wave to form a scroll spiral with multiple windings.
This vortex also looks a lot like a tubular ring, which is a vortex of a different class. I believe it is more likely that this vortex is a scroll with only one winding and not a tubular ring because of the way that it connects to the water surface. A tubular ring is a stand-alone vortex that does not visibly connect to any other vortices.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |






_ByNASAAndESAAndSTSclAndWKeel_PublicDomain.jpg)
