The Transformation Sequence
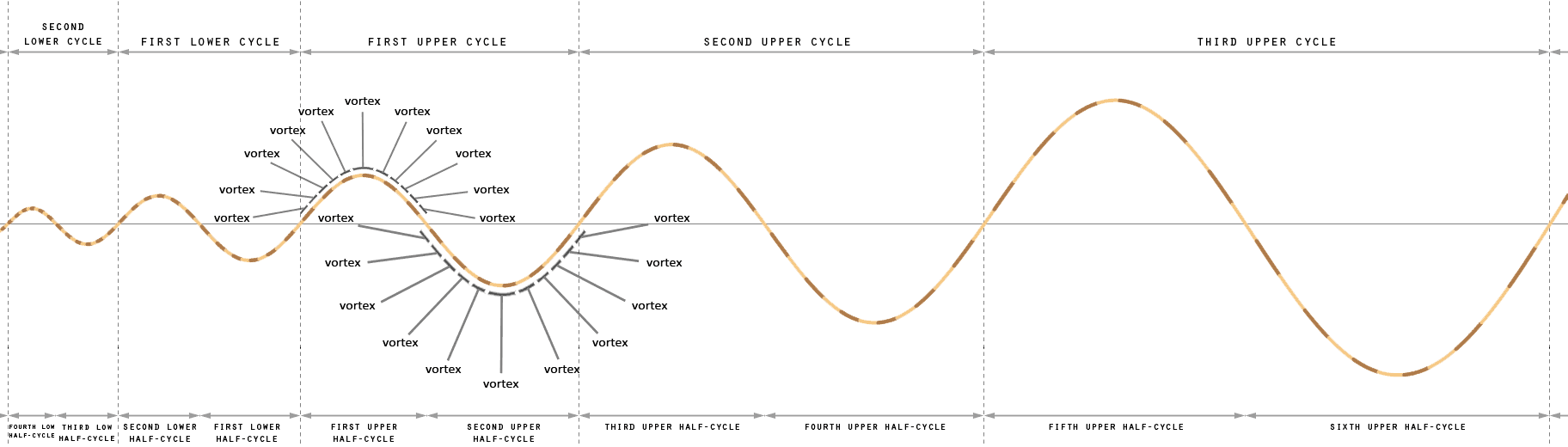
What you see in the image below is a huge vortex that is composed of many different smaller vortices. Most of these vortices have been known for a long time (fluid mechanics is a field of science that studies them, but only the ones that have a rotation are called vortices). But some of the vortices in the sequence were unknown until now, or have not prior been classified as vortices. The existence of some of these vortices are revealed from similarities found in other parts of the sequence. What was also unknown until now is that all these vortices fit together like a great puzzle, in which their order follows a logical pattern. The strong continuity of the transformation sequence is one of the reasons that I was able to solve this puzzle and fill in some of the gabs prior to finding the actual pieces.

Try to picture an imaginary mirror line through the center of the image. The left and right side look identical, only mirrored. There are two versions of each vortex, one being a mirror image of the other. In one the movements are left-turning where in the other these same movements are right-turning, and vice versa.
The line through the center of the image above is not the only line that divides left-turning vortices from right-turning vortices. There are more of these mirrors and they always run through one vortex that is classified as a bridge vortex. These bridges are what connects these two halves in various locations within the sequence. Because there are multiple mirrors, a vortex can be mirrored twice, the consequence of this is that some vortices have four of these mirrored version of themselves instead of just two (one such vortex is the called the scroll ring).
The EM Crossing Locations
There are multiple locations in the transformation sequence where it almost seems that the sequence has a beginning or an end (it does neither, the sequence is infinite). One of them is called the zero point, another is called the infinity ring. Do not let yourself be misled into thinking that the vortices end there. These locations are transition spots between the positive and negative side of the sequence, and they are locations in the sequence where the vortex movement is purely electromagnetic. For this reason these locations are called EM crossing locations (EM = electromagnetic). In these locations some of the wave characteristics either cross from small positive to small negative values or flip from positive high number to negative high number. (The name infinity ring is a bit misleading because values become large there not infinite). The zero point you will find by zooming in on the swirl, it is the EM crossing location that connects to the spire. The infinity ring you will find by zooming in on the revolute, it is the EM crossing location that connects to the omega ladder (there is actually one more unknown vortex between the omega ladder and the infinity ring). The zero point is a (volume-less) point and the infinity ring is a (volume-less) circle. In the image below you only see one half of each infinity ring, that is because you are looking at a cut-through model of the sequence.
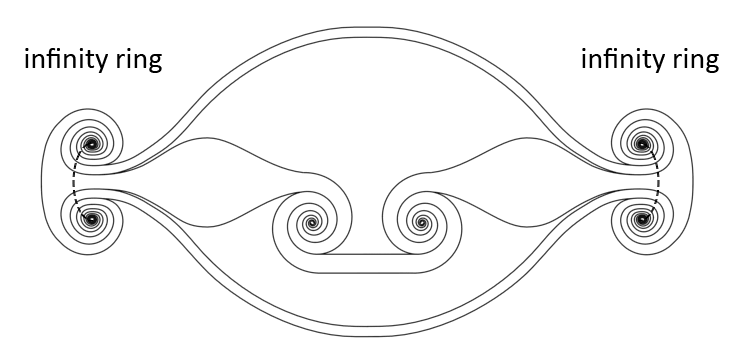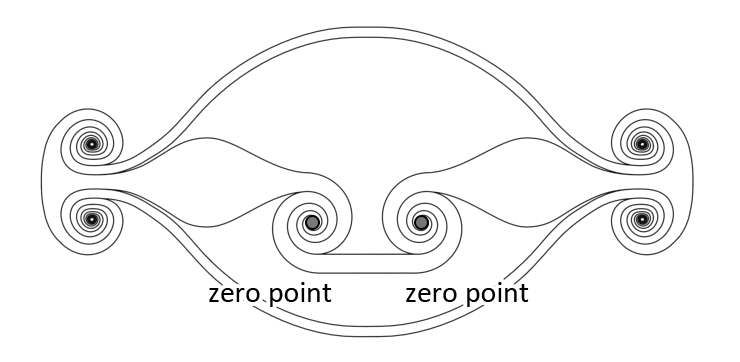
Do not confuse these two locations with vortices. The zero point and infinity ring are locations within the sequence, they are not physical objects. Same as the south pole in Antarctica, which is a geographic position, not a physical object.
There are vortices right before an EM crossing location, and there are vortices right after an EM crossing location. Yet the vortices that lie after a crossing location have different characteristics from the vortices that lie before the crossing location. At the same time they also share characteristics with the vortices on the other side of the EM crossing location. The EM crossing locations are almost like mirror points. Yet this mirror, unlike the one that reflects the left and right turning side of the sequence, is not a mirror that creates an exact mirror image of the shapes. The vortices look different on both sides of the EM crossing location, yet the characteristics are transformed, reversed or inverted, into a new form. One could say that the EM crossing locations are transformation transition spots. Two of these spots are the zero point and the infinity ring.
The Cycles of the Transformation Sequence
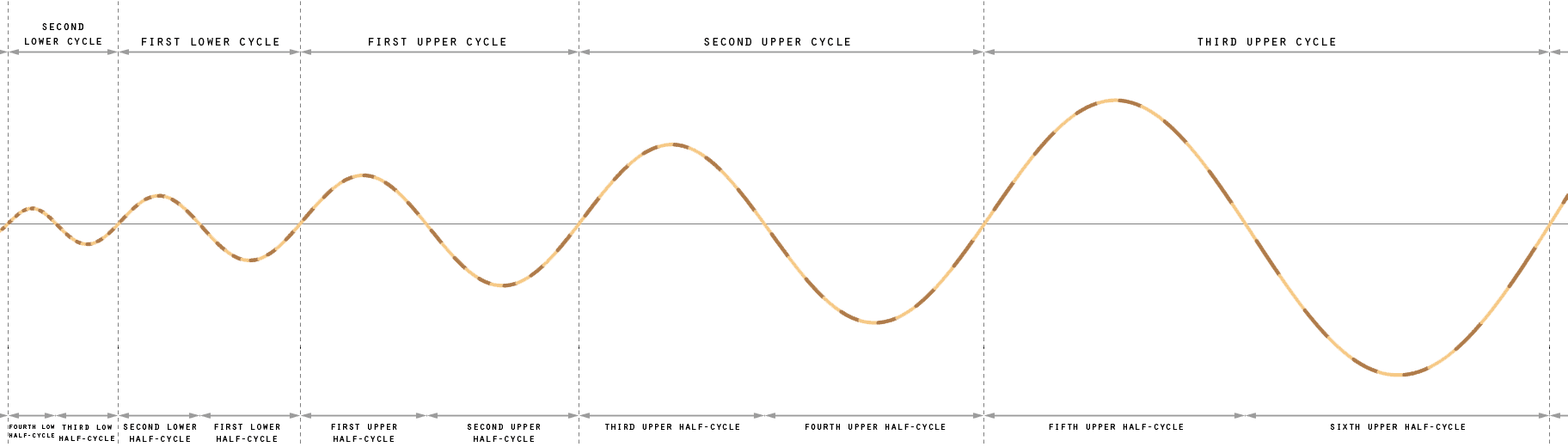
The transformation sequence is arranged into multiple cycles. The image at the top of this page only shows vortices from one cycle. There are more cycles beyond and prior to this cycle that can be plotted out as a progressively growing sine curve. Each cycle of the sequence is unique and the vortices in each of these cycles look completely different. You can click on the image below to get a bigger view.
The image at the far top of this page actually only shows the vortices from one half-cycle. The other half-cycle is located below the centerline and has different looks and characteristics than the half-cycle above the centerline. A half-cycle forms the half of one sine curve, from one position where it crosses the centerline to the next position where it crosses the centerline.
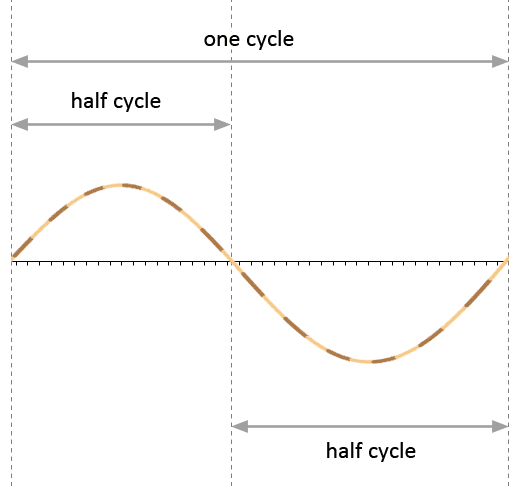
The electromagnetic spectrum is located on the centerline itself, this is also the line on which the EM crossing locations are located. Both the zero point and the infinity ring are positions where the curve crosses the centerline. Both these locations succeed each other at the start and end of the first half-cycle.
On the path that this transformation curve follows lie many different vortices that succeed one another. Together they can form a connected sequence. The image below gives an indication on which position vortices might be within one single cycle of the sequence. It is not known at this moment exactly how many vortices exist in each sequence. It could be that the number is equal in all cycles, yet it is more likely that the number increases with each progressive cycle.
The distance from the centerline to a position of a vortex indicates the volume of that vortex. As the transformation curve progresses, the vortices go back and forth between becoming larger and smaller in volume but in each cycle the overall volume of the vortices becomes larger.
![]() At any time when you are browsing through the pages on this website you can view these same transformation cycles in a pop-up screen within your browser. All you need to do is click on the far left icon at the upper right corner of this page. It will be useful later because more details about these cycles will be explained and at time you might need the help of this graph to enable you to understand or remember all the information.
At any time when you are browsing through the pages on this website you can view these same transformation cycles in a pop-up screen within your browser. All you need to do is click on the far left icon at the upper right corner of this page. It will be useful later because more details about these cycles will be explained and at time you might need the help of this graph to enable you to understand or remember all the information.
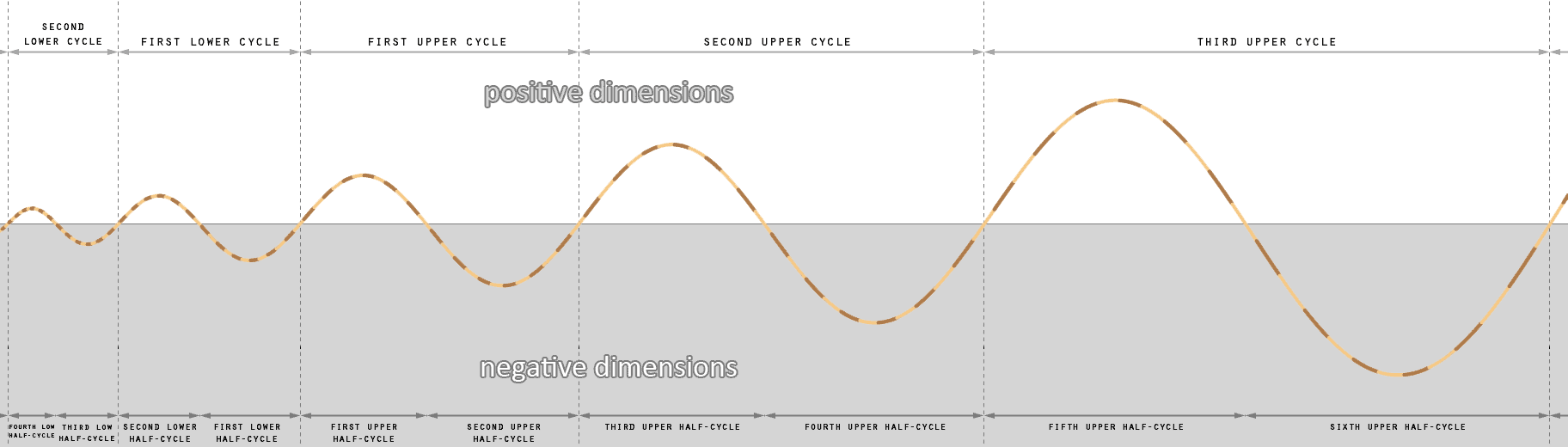
Negative and Positive Dimensions
There is a significant difference between the sequence above the centerline, and the sequence below the centerline. The region above the centerline is where we find the positive dimensions. The region below the centerline is where we find the negative dimensions. The characteristics of matter, waves, and vortices are different in both these opposite sides. The sine curve of the transformations sequence forms a continuous movement between this positive and negative side of the sequence. The centerline is called the EM spectrum line (the line is actually a plane, but we will get to that later).
When a vortex movement in the positive dimensions crosses the EM spectrum line then that movement becomes negative dimensional. Negative means that some of the characteristics becomes negative, and that matter behaves according to those negative conditions. The EM spectrum is the location in the sequence where the values on one side are positive and the values on the other side are negative. On the EM spectrum line itself the values are either zero, or flip from a high value to a low value or vise versa. Two properties of a vortex that are opposite of each other in both sides of the sequence are the volume of a vortex, and time velocity. The positive dimensions have a positive time velocity, the negative dimensions a negative time velocity. The consequences of this and what it means will be explained on the page about time.
The volume of a vortex is positive on the positive side of the sequence, and negative on the negative side of the sequence. The size of a vortex is something different then the volume of a vortex. For the size of a vortex there does not appear to be a value below zero. Scaling down means that values become smaller and smaller on a logarithmic curve that can go on for ever. But the volume of a vortex does have a value that can go to zero and beyond.
There is no method to measure a negative volume. We can measure the size of a negative dimensional vortex, but our ways of measuring to not distinguish between a positive and a negative value. We can only detect positive values, we have no physical tools to do determine that a volume is negative. Determining whether matter or movement is negative dimensional is achieved by other observation methods. By looking at visual appearance and other characteristics. Negative dimensions is where we find plasmas. If we know that something is made of plasma, we know that its volume is negative (inverted). The positive dimensions is where we find the solid, liquids and gases. When something is made of a solid, liquid or gas, we know that its volume is positive (not inverted).
If we go back to the image of the sequence at the start of this page, the connected vortices in that image are all positive dimensional vortices. All those vortices belong to the first forward half cycle. This was only a short introduction to the negative dimensions. In the first coming seven pages the focus will be most on the positive dimensions, after that the topic will shift to the negative dimensions.
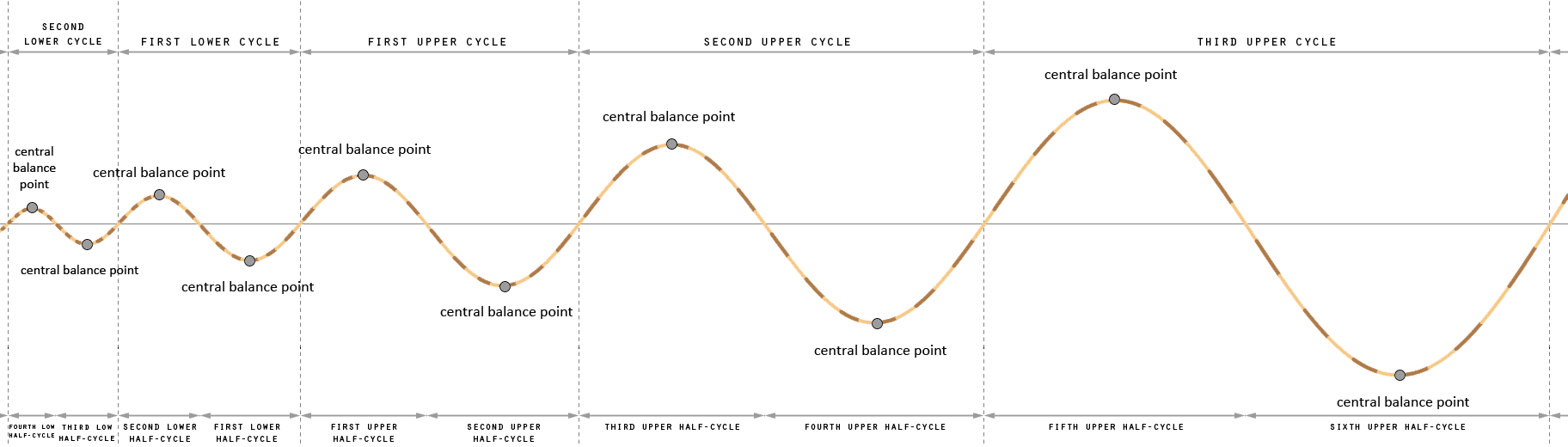
Central Balance Points
The transformation sequence also has a center, a middle, two for every cycle, one in the center of each positive half cycle and one in the center of each negative half cycle. These are are called central balance points. One of them is located at the middle of the bulb vortex, which is the central balance point on the positive side of the sequence, which is also called the main balance point. The other is located in the next half cycle at the middle of the inward dimensional antipode of the bulb, which is on the negative inward side of the sequence.
The Main Balance Point
The central balance point within the first positive half cycle of the sequence lies at the center of the bulb, at 3.0D, where its periphery (thickness of the vortex) reaches the largest radius. This point is also called the main balance point of the sequence. This main balance point is the precise center of that part of the sequence. This is where the dimensionality level is neither high or low. There can be two versions of that balance point because they can be mirrored by a bridge, but these two still classify as the same balance point.
Thus on the main balance point itself lies the center of one vortex, and this is also true for all the other balance points. Those locations are located on the center position of a vortex.
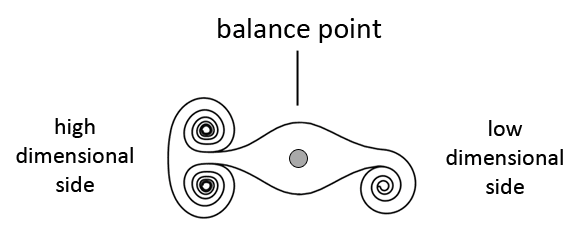
Once I understood that this was the precise center of the sequence, it became easier for me to determine how many dimension levels there were on the higher side of the sequence and which vortices were still missing. This is because once you know all the dimension levels on one side of the bulb, you also know a lot more about the vortices that are supposed to be on the other, opposite side of the bulb. Both these are opposite images of each other, antipodes. Both located within the same half cycle.
Contraction and Expansion
An increase in dimensionality is called expansion. A decrease in dimensionality is called contraction. Dimensionality is determined by the total amount of field that is included in the projection of the onefield. And this amount of field is determined by the scale size, cycle number, and the number of dimension levels that are included in the projection, plus other properties.
These two words will be used continuously throughout this website. Contraction and expansion is one of the key principles taken from the yin yang theory, although this link with dimensions has only been established within the infinity theory.
CONTRACTION AND EXPANSION = A CHANGE IN THE STATE OF PROJECTION SO THAT A SMALLER OR LARGER REGION OF THE ONEFIELD IS PROJECTED ONTO A SPECIFIED REGION WITHIN OUR PHYSICAL WORLD
At all times you should be aware that when an extra axis is added to the projection, in most cases it grows steadily until the axis is fully added in the projection. This is not possible in the Cartesian coordinate system, where you can only add or remove an axis instantly. So in the projected universe, a dimensional axis can be added partially to the other axes, in fractional numbers.
This contraction and expansion is also called the yin yang movement, where contraction is yangization, and expansion is yinization. The words yangization and yinization are not found in dictionaries, but those words are used on this website.
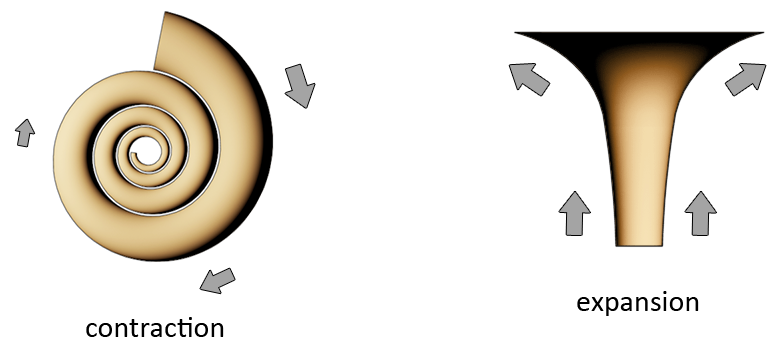
Above you can see two vortices. One is called a swirl, the other is called a pylon. Both these vortices belong to the same half-cycle. The swirl is rotational vortex and the pylon is a non-rotational vortex. The swirl makes a flow movement from the larger end to the small end while the pylon makes a flow movement from the small end to the larger end. In both these examples, the larger end is where dimensionality is the highest. The movement of the swirl is called contraction, while the movement of the pylon is called expansion. There are also rotational vortices where the movement is an expansion instead of a contraction. And there are also non-rotational vortices in which the movement is a contraction instead of expansion.
By looking at the shape of the vortex we can in many cases identify which type of vortex it is. When we know that the first vortex is a swirl and the second vortex is a pylon, we also know that one is low dimensional, thus linked to a tight wave, and the other one is high dimensional, thus linked to a more flexible wave. High and low dimensionality also influences how vortices move, and how matter behaves.
| Contraction | Expansion |
| Decrease in amount of field that is projected from the onefield (either by decrease in angle of projection, decrease of scale size, decrease of cycle number, or change of another property) | Increase in amount of field that is projected from the onefield (either by increase in angle of projection, increase of scale size, increase of cycle number, or change of another property) |
| Peripheral movement from high end to low end of vortices | Peripheral movement from low end to high end of vortices |
| Tightning, hardening | Loosening, softening |
| Increase in velocity | Decrease in velocity |
| Fusion of peripheral movements | Diffusion of peripheral movements |
| Pulling force | Pushing force |
| Acceleration of time | Deceleration of time |
The table above lists a few characteristics that apply for when dimensionality increases or decreases. This table is about the direction of movement. This direction of movement determines whether the attributes on the left or right side of the table come into play. If you look at the top right corner of the screen, you will find an orange icon in the shape of a yin yang symbol. You can click any time you want on this icon and it will open a small window that shows the same table as the one above, plus more. Do use that icon whenever you need to, it will help you understand better what's to come.
The Yin Yang Theory
Some of the basics of the infinity theory has been derived from the yin yang theory. This ancient philosophy is more than 2000 years old and lies at the origins of many branches of classical Chinese science. Not that much has changed about the theory since it was developed, and part of it is kept in a void because of some of the missing scientific explanations of the nature of yin and yang. The infinity theory now brings a wider understanding of what the scientific explanation of yin and yang is. It brings our understanding of these two fundamental universal opposites to a whole new level of understanding and adds new insights to the theory that can help it merge with a more modern approach of science.
One of the things you might be aware of is that the yin yang theory is still used today as a primary guideline of traditional Chinese medicine. But there are different versions of the yin yang theory, and the version that I chose to use on this website is not the version used by Chinese medicine. The version I use was devised by George Ohsawa early in the 20th century and it is a version that is less known than the Chinese version. This variation of the yin yang theory focuses on contraction and expansion which is not the main focus in the Chinese version. Not all of Ohsawa's version correlates with the Chinese version, some of it is the reversed opposite to that of the Chinese version. I have not found a person that can explain these differences, but there should be a logical reason for this. That reason could perhaps be found in the scale levels, which are mentioned further down on this page. This website could one day possibly lead the way to an understanding of these differences.
The reason I started out with this version is simply because that is the only version that I've learned. It would take me too much time to learn a whole other version of the yin yang theory before the launch of this website, and secondly, I did not want people to think that the purpose of this website is to promote Chinese medicine. I do not oppose to Chinese medicine, but I simply know nothing about it. So I chose to use this lesser known version, which is hardly used today. Nevertheless, I do invite people who are familiar with the Chinese version of the yin yang theory to join the forums on this website, so they can attempt to translate all the knowledge on this website to the Chinese version of the yin yang theory, so that it fits with the theory just as Ohsawa's version. There's a great chance that we will find more clues and more puzzle pieces once we know how the infinity theory correlates with the Chinese yin yang theory.
The yin yang theory does not mention different basic types of vortices or fluid motions or anything about the transformation sequence, those findings are new. This could make a significant difference in how we are now able to apply the theory of yin and yang to both scientific approaches and everyday situations. Nearly all the findings that are presented on this website are new, yet in some occasions the origin of a finding is closely connected to existing knowledge from the yin yang theory. Whenever possible I will mention the yin yang theory to explain the origin of a particular idea or finding.
If you already posses some knowledge about the yin yang theory, and you read something on this website that is inconsistent with what you think you know about the yin yang theory, then remember I'm using Ohsawa's version, not the Chinese version. In this version yangization is contraction, yinization is expansion. Something that is yang is contracted, something that is yin is expanded. Those are some of the most important things to know. I will write a page about the yin yang theory one day to explain some more issues. If you do not yet know anything about the yin yang theory then you can still understand what is written on this site. The infinity theory is written in a way that anyone can understand contraction and expansion, without the use of the words yin and yang. But it does give you a fast start when you're already familiar with these concepts.
What is important to know is that the main balance point, at the center of the bulb, is the yin yang balance point. This is where movement is neither yin or yang (actually, it can still be yin or yang relative to something else). This location in the sequence is determined by our human perception. For other lifeforms this point can be located somewhere else. There are more phenomena within the infinity theory that correlates or explains the theory of yin and yang, these will be pointed out later.
|
George Ohsawa
George Ohsawa (Yukizaku Sakurazawa, 1893-1966) is recognized as the founder of macrobiotic principles and lifestyle practices. By the time that he was eighteen years old, three of his family members, his mother, younger brother and younger sister, had all died of tuberculosis. At that time he was told by the doctors that there was not much they could do to stop his illness, there was little chance that he would survive. Determined not to succumb to the same fate as his beloved ones, Ohsawa began searching for alternative theories of health. He started eating a diet of brown rice and cooked vegetables, based on Sagen Ishizuka’s (1850-1910) theory of balancing mineral salts, the early heaven’s sequence of the I-Ching, yin and yang, and other ancient Eastern concepts. Soon the tuberculosis disappeared. He lived to the age of 73, devoting his life to teaching macrobiotic theory and writing on science, ethics, religion, and philosophy from a macrobiotic point of view. George Ohsawa introduced the oriental concept of health to Westerners in the mid-20th century, writing about 300 books in Japanese and 20 in French during a 40-year period. He was a scholar, healer, businessman, educator, and poet.
But most of all, he was a Far Eastern philosopher who taught his version of the ancient Chinese philosophy of yin and yang. When he was in France, he first applied his philosophy to physical science. Later, he worked to apply it to many areas such as nutrition, diet, medicine, chemistry, ethics, religion, education, and business, as well as lifestyle. Ohsawa also collected many of the great thoughts from East and West, from ancient to modern, and applied them to various aspects of living. His interpretations, based on the unifying principle of yin and yang, were devised to guide people in a practical way towards improvement of health. |
George Ohsawa should be mentioned here because it is his version of the yin yang theory that is used as a basis for the infinity theory, as a starting point. The yin yang theory itself is thousands of years old, yet different from the one devised by George Ohsawa. George Ohsawa developed an adapted version of the yin yang theory that focuses on contraction and expansion. Ohsawa's version of the yin yang theory is significantly different from the Chinese version, some of it even seems reversed. What is yin in one version is yang in the other version. Some call Ohsawa's version the physical version and the Chinese version the metaphysical version.
There are different ways one can find the correct answer. There are different routes one can take to solve a puzzle. It is not completely required to know the yin yang theory to be able to solve the puzzle of the transformation sequence. But I myself, having no degree in physics or mathematics, would never have been able to solve it without knowing the yin and yang theory of George Ohsawa. There were too many puzzle pieces to be found in there that I would not be able to interpret correctly without.
High and Low Dimensional
The words 'high dimensional' and 'low dimensional' are pretty straightforward when we look at the cycles of the sequence. High dimensional is anything above a central balance point. Low dimensional is anything below a central balance point. When we talk about the negative dimensions, however, then low dimensional is anything above the central balance point, and high dimensional is anything below a central balance point. Thus high dimensional is either a high positive number or a high negative number, and not just solely a high positive number.
Characteristics of Dimensionality
Below is a table that sums up the most basic characteristics of high and low dimensionality. I will often refer back to this table when explaining certain phenomena. The table is short and simple, it won't be long before you will understand the logic of why something is high dimensional and something else is low dimensional. Only in the beginning you will need the help of this table.
| High dimensional (Yin) | Low dimensional (Yang) |
| General Characteristics | General Characteristics |
| Expanded | Contracted |
| Loose | Tight |
| Sensitive to external motion | Insensitive to external motion |
| More projected field | Less projected field |
| Number of dimensions being projected is higher than that of our human perception (greater than 3D). Thus complexity is concentrated over a smaller volume by projection. | Number of dimensions being projected are lower than that of our human perception (lesser than 3D). Thus complexity is spread out over a larger volume by the projection. |
| More asymmetry | More symmetry |
| Slower movement | Faster movement |
| Time runs slower (macrocyclic effect) | Time runs faster (macrocyclic effect) |
| Vortex Characteristics | Vortex Characteristics |
| Diffused | Fused |
| High number of meridians | Low number of meridians |
| Complex movement | Simple movement |
| Less friction | More friction |
| Long vortex lifespan | Short vortex lifespan |
| Curved | Angular |
| Large scale size | Small scale size |
| Wave Characteristics | Wave Characteristics |
| Loose | Tight |
| Slow propagation | Fast propagation |
| High frequency waves | Low frequency waves |
| Short wavelength | Long wavelength |
| Directional peripheral waves | Spherical peripheral waves |
| Short range | Long range |
| Characteristics of Matter | Characteristics of Matter |
| Lighter | Heavier |
| Soft | Hard |
| Intangible | Impenetrable |
| Flexible / non-constricted | Rigid / constricted |
| Less friction | More friction |
| Higher compressibility | Lower compressibility |
| High Reynolds number | Low Reynolds number |
Some of the entries in the table above were taken from the book Makrobiotiek,
by Michio Kushi (dutch edition).
When something is high dimensional, that does not mean that all of its characteristics are described in the left side of the table, and when something is low dimensional, not all its characteristics are found in the right side of the table. Only some characteristics match with the table, not all simultaneously. A vortex or a volume of matter can be low or high dimensional in different ways. There are different forms of yin, and different forms of yang.
![]() If at any time during reading the pages on this website you wish to view this table you can click on the yin yang symbol at the upper right corner of the page. It might be useful to do so at times because you will encounter many phenomena on this website that are influenced by these properties. The table will help you understand better what the difference is between high dimensional and low dimensional.
If at any time during reading the pages on this website you wish to view this table you can click on the yin yang symbol at the upper right corner of the page. It might be useful to do so at times because you will encounter many phenomena on this website that are influenced by these properties. The table will help you understand better what the difference is between high dimensional and low dimensional.
Lets take one quick example so you get a bit of a feel as to how the logic behind this table works. Lets consider the states of matter. When you look at table one and consider these three states of matter: gas, liquid and solid, then it is quite easy to conclude that liquids are lower dimensional than gases and solids are lower dimensional than liquids. Solids are harder, less penetrable, heavier, water is more flexible / loose, gas is intangible and lighter, etc. The states of matter are easy to arrange in the correct order in terms of dimensionality. It is too early to add the fourth state of matter, plasma. Plasma belongs to the negative side of the sequence and will be discussed later.
This example works because there's no mention of organic life and organic matter. The characteristics that are summed up in the table above strongly apply to all inorganic matter, but the rules do not seem to fully coincide with the characteristics of organic matter. Those characteristics are harder to determine because organic matter appears to be a combination of several dimension levels. But for now this table is sufficient for most of the examples found on this site.
Spirals vs Helices
Most people know the difference between a spiral and a helix. Still it happens sometimes that a helix is mistaken for a spiral. There are many pages on the internet on which observations are made in which a certain shape is called a spiral, while it is in fact a helix. Spirals and helices are mentioned often on this website, so it is important to avoid mix-up.
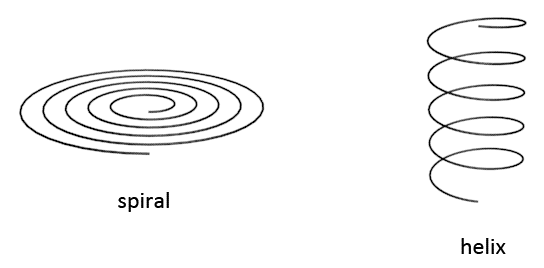
The vortex whose shape most resembles a helical shape is called the helix tunnel, which will be introduced later. The two shapes above are the most basic shapes of a spiral and a helix, yet there are more complex spiral and helix shapes found in nature that at first glance do not appear to be spirals and helices. It is only when the spiral or helix becomes more complex that its shape becomes harder to classify. A shape can sometimes also be a blend of a spiral and a helix.
Scale of Vortices
The scale of a vortex is a very important factor to consider and you need to be constantly aware of this factor whenever you try to understand phenomena that are the result of vortex movement and the waves that connect to these vortices. But the consequences of the scale of a vortex are not that hard to understand. I already mentioned how different waves in the onefield that have a very different dimensionality cross over each other without colliding with one another. One way to determine how high dimensional (yin) a vortex is, and thus how high dimensional the wave is that connects to the vortex, is by observing the shape of the vortex. Determining its type gives a first important indication of its dimensionality. But another factor that you need to know on top of that is what size the vortex is.
When you compare two vortices of the same type, then you should know that the bigger the vortex, the higher the dimensionality. Smaller vortices of the same type have lower dimensionality. Thus dimensionality varies on every scale and even when two vortices are of the same type, they can still differ greatly in dimensionality if their size is very different. One way you can find out that this rule about the scale of vortices is correct is by observing the speed of movement of different vortices of the same type.
 |
 |
 |
| Image by Langley Research Center of the United States National Aeronautics and Space Administration (NASA) | Image by National Ocean and Atmospheric Administration | Image by European Space Agency & NASA, (ESA/Hubble) |
One of the things you will notice when you observe vortices in our world is that the larger a vortex is, the slower it moves, and the smaller the vortex is, the faster it moves (this comparison applies to two vortices of equal type). Large scale is higher dimensional thus time runs slower, small scale is lower dimensional thus time runs faster. One example of this is a swirling vortex behind an airplane vs a hurricane vs a spiral galaxy. All three of these vortices are of the same type (the swirl), but they all move at very different speeds. The airplane vortex makes a couple of centripetal rotations in just a few seconds, a hurricane makes a couple of rotations in a full day and a spiral galaxy makes a couple of rotations in millions of years. The large and small scale also correlates with all of the other attributes in the table of properties.
Macrocyclic, Mesocyclic and Microcyclic
Because of the importance of different scales, I had to come up with a scale system so that with just one word people know enough about the scale of an object or phenomenon so that they can understand a certain situation. It is not a method for describing the exact size of an object, but only to describe by category so that important features can be explained. For this I came up with a simple system. What I've done is divide the universe into three levels: macrocyclic scale, mesocyclic scale and microcyclic scale. We want to use only the number of categories that we need to explain things, not more than that. And often these three categories are sufficient.
| Macrocyclic Scale | Anything that is astronomically large |
| Mesocyclic Scale | Anything between macrocyclic and microcyclic |
| Microcyclic Scale | Anything too small to be seen with the naked eye |
The scale of these three different levels refers to the transformation sequence, and how the exact same movements that occur within the different cycles of the sequence can occur at different sizes. A vortex that is observed at a small cyclic scale level can also exist in a larger cyclic scale level. The cycles of the transformation sequence can exist at a small scale, or at a large scale, and basically any size in between. So far there does not appear to be restrictions in particular sizes or ranges of scales. For the transformation sequence, all sizes are possible.
Basically you could say this: the mesocyclic scale is where we ourselves are. It is the size of things that are relatively close to the size of our own human bodies, but within a very wide range. Both the microcyclic and the macrocyclic scale belong outside this range. The microcyclic scale is that which is much much smaller than us. And the macrocyclic scale is that which is much much larger than us.
The table below shows the relation of these three new scale levels with current conventions to indicate a particular size. Currently there does not exist a good system that is arranged in steps and with which one can categorize any random size. Therefore the only solution was to come up with a new method.
| Astronomical | Extremely large, that which is studied in astronomy | Macrocyclic Scale |
| Megascale | At least 1000km in length | Macrocyclic Scale |
| Macroscopic | Visible with the naked eye | Mesocyclic Scale & Macrocyclic Scale |
| Mesoscopic | Typically in the range of 100nm to 1000nm | Microcyclic Scale |
| Microscopic | Not visible with naked eye, visible with microscope | Microcyclic Scale |
| Quantum Realm | Distances of 100 nanometers or less | Microcyclic Scale |
| Nanoscopic | Usually cited as 1-100 nanometers in size | Microcyclic Scale |
These scale levels are equivalent to each other. Each level is just as important to understand when trying to understand the infinity theory, and each scale level exists under the same set of rules. The rules of the infinity theory apply to the macrocyclic scale in the same way as they would apply to the mesocyclic scale and the microcyclic scale. The different scale levels might look and behave different, because smaller sizes are lower dimensional than that which has a larger size, but both still operate under the same set of rules. We can learn a lot from the macrocyclic scale by observing the mesocyclic scale, and vice versa.
One of the rules that applies to the different scale levels is that movement in one of the major scale levels has a tendency to result in an opposite movement in a subsequent scale level. This is because dimensionality always seeks a balance. For instance, when dimensionality increases on the mesocyclic scale, then at the same time, dimensionality decreased locally on the microcyclic scale. This is true except for when certain conditions do not allow this to happen, for example when the pressure of the medium is too high or too low to allow the change in dimensionality. In those cases, something else will change that will result in a (apparently somewhat less favorable) balance. Some examples of this are presented on the page about temperature. But there are many more examples spread out through these pages that show this rule in action. Another example of these opposite movements on subsequent scale levels are the negative dimensions vs the positive dimensions. When dimensionality on a mesocyclic scale is positive (which is true in most cases when looking at inorganic matter here locally on earth) then dimensionality on a microcyclic scale has a tendency to be negative. By looking at the examples mentioned on this website it appears that these opposite movements of different scale levels only apply to the three major scale levels: microcyclic scale, mesocyclic scale and macrocyclic scale, and not to more than three levels. But there are some cases where it is required to divide either the macrocyclic or the microcyclic scale level into more levels so that the rule applies correctly. There are more than three scale levels, we need to acknowledge this before we can understand all the phenomena that occur as a result of the existence of these different scale levels.
EVERY MOVEMENT (ACTION) COINCIDES WITH AN EQUIVALENT OPPOSITE MOVEMENT (REACTION)
When you look at a single or a few elements, then what one could observe is imbalance. But when you look at the whole picture, and include all the elements, then there's always balance. You might for instance observe an imbalance in the mesocyclic level, but this observation of balance becomes an observation of balance when one would include the observations of the microcyclic level. The mesocycles could be where the action takes place, and the microcycles where the reaction takes place, or the other way around. This law of action and reaction is always effective in our universe. But it is not always so that the reaction movement is clearly visible or easily understood.
There is a possibility that these three major scale levels form the missing link between the Chinese version of the yin yang theory, and the version devised by George Ohsawa. It could be that the differences between the two theories can be explained with these scale levels. George Ohsawa's version appears to focus on movement on the mesocyclic scale, while I suspect that the Chinese version of the yin yang theory focuses on movement on the microcyclic scale, without that people were aware of that. The first one focuses on the visible movement, and alterations in form and shape, while the latter one focuses on the non-visible movement, thus being dependent on other factors like color and temperature for observation (but this microscopic world is to some extent visible today using microscopy and other methods). This would also explain the contrary directions of the movements in these two theories. If this proves to be true than both these theories could be joined together, and thereby grow into one larger, more complete theory.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |