Vortices and Dimension Levels
At this present-day it is not known how many dimension levels in our universe can be observed or detected by us humans. The total is assumed to be infinite, but it is likely we can only find a limited number of them. A limited number within a limited range have been found and classified, but there are way more vortices that are still waiting to be discovered.
The vortices are divided into types and classes. A type is a vortex with a unique shape and movement. And a class is a list of types which share similar characteristics. There are many more vortex types than vortex classes. Each vortex can be addressed by a unique name, and so does every vortex class have a unique name.
Most vortices that we know exist today did not have a specific name, yet there are clearly basic types of vortices that should be identified as a basic type and therefore should be named. So I gave a name to each of the vortices in the sequence so that it is easily understood which vortex I'm referring to at any given moment. There are a few names that are already in use today.
The vortex that I call the 'revolute' and the vortex that I call 'scroll ring', are both often called a 'vortex ring'. I renamed them because I needed to have one name for each of them, to identify them as separate types. The word 'vortex ring' can still be used at situations where a clear distinction between the two types is not necessary. Helicones are sometimes called 'tornado-like vortices'. The aureole belt and the laminar belt are under some conditions called 'condensation rings' (here too, there's no distinction between the two types, yet this distinction is required). Some scroll rings that are not fully formed are called 'horseshoe vortices'. Sometimes the vortices are given a specific name when they are found in a specific medium. For example, a suprabell made of water is called a liquid bell.
The names that I came up with are not all permanent. Some I'm pretty content with and some might need to be replaced with better alternatives later. For now they are all right to work with. Only time will tell whether each of these naming conventions will remain. It is not me alone who will decide how these vortices will be named. Anyone who can come up with an adequate name for a particular vortex can submit his/her idea in the forums. Perhaps the best thing for me to do is to start a poll one day in which anyone can participate in naming the vortices.
Below is a table that lists all the vortices and their dimension levels that have been found so far, including some of the gabs that indicate the locations of unknown vortices that still need to be found. Every vortex is linked to a specific dimension level. The vortices are listed from high dimensional (yin) to low dimensional (yang).
The 5th column within the table tells if the vortex is either rotational or non-rotational. Although all these different shapes of movement are called vortices, only some of them are visibly rotational. They are only indicated as rotational if the sum movement, which is the visible movement of the vortex, is truly rotational. They are not indicated as being rotational if there are hidden roational movements that when added together form a non-rotational observable movement. They are also not called rotational if the movement does not show a rotation but it still expresses some of the same characteristics as a vortex that has a rotation. Do not worry yet about what state of equilibrium is, that will be explained later. I will discuss each of these vortices in detail.
| Type | Dimension | Cycle | Class |
Rota- tional |
State of Equilibrium |
| Level3 Fallback | -4.75D to -4.25D | 2nd | Unknown | no | Unknown |
| Level2 Fallback | -5.75D to -5.25D | 2nd | Unknown | no | Dye |
| Unknown | -6.0D to -5.75D | 1st | Half a spiral | Unknown | |
| Electricity | 6.0D <> -6.0D | 1st | EM Spiral | yes | - |
| Unknown | 5.75D to 6.0D | 1st | Half a Spiral | Unknown | |
| Unknown | 5.75D (CW<>CCW) | 1st | Outer Bridge | Unknown | |
| Unknown | 5.75D | 1st | Exterior Tunnel | Unknown | |
| Unknown | 5.75D | 2nd | Bell | Unknown | |
| Omega Ladder | 5.25D to 5.75D | 1st | Ladder | no | Unknown |
| Omega Bridge | 5.25D (Inw to Outw) | 1st | Inner Bridge | no | Unknown |
| Ultraduct | 5.25D (Inw to Outw) | 1st | Interior Tunnel | yes | Unknown |
| Mirage | 5.25D | 2nd | Disk | no | Silver |
| Scroll Ring | 4.75D to 5.25D | 1st | Spiral | yes | Saturated Fat |
| Wake Belt | 4.75D (CW<>CCW) | 1st | Outer Bridge | no | Slime |
| Bubble | 4.75D | 1st | Exterior Tunnel | no | Soap |
| Tubular Ring | 4.75D | 2nd | Bell | yes | Unknown |
| Aureole Belt | 4.25D to 4.75D | 1st | Ladder | no | Unknown |
| Laminar Belt | 4.25D (Inw to Outw) | 1st | Inner Bridge | no | Unsaturated Fat |
| Gyroduct | 4.25D | 1st | Interior Tunnel | yes | Vulcanized Rubber |
| Capillion | 4.25D | 2nd | Disk | no | Tin |
| Revolute | 3.75D to 4.25D | 1st | Spiral | yes | Gelatin |
| Revodome | 3.75D | 2nd | Bell | yes | Unknown |
| Cradle | 3.75D | 1st | Exterior Tunnel | no | Chicle |
| Pilaster | 3.75D (Outw to Inw) | 1st | Outer Bridge | no | Petroleum |
| Pylon | 3.25D to 3.75D | 1st | Ladder | no | Unknown |
| Lentillion | 3.25D | 2nd | Disk | no | Gallium |
| Exobar | 3.25D | 1st | Outer Bridge | no | Pitch |
| Bulb | 2.75D to 3.25D | 1st | Spiral | no | Air |
| Vessel | 2.75D | 2nd | Bell | no | Unknown |
| Exoduct | 2.75D | 1st | Exterior Tunnel | no | Natural Latex |
| Endobar | 2.75D | 1st | Inner Bridge | no | Unknown |
| Amplicone | 2.25D to 2.75D | 1st | Ladder | no | Dust |
| Mercury Belt | 2.25D | 2nd | Disk | yes | Mercury |
| Troth | 2.25D (CW<>CCW) | 1st | Outer Bridge | Honey | |
| Swirl | 1.75D to 2.25D | 1st | Spiral | yes | Water |
| Unknown | 1.75D | 2nd | Bell | Unknown | |
| Whirlpit | 1.75D (Inw to Outw) | 1st | Exterior Tunnel | yes | Clay |
| Helibar | 1.75D (Inw to Outw) | 1st | Inner Bridge | yes | Earth |
| Helicone | 1.25D to 1.75D | 1st | Ladder | yes | Marl |
| Hyperbelt | 1.25D | 2nd | Disk | yes | Unknown |
| Enexus | 1.25D (CW<>CCW) | 1st | Outer Bridge | no | Resin |
| Disc | 0.75D to 1.25D | 1st | Spiral | yes | Gypsum, Some Metals, Wood, Bone |
| Unknown | 0.75D | 2nd | Bell | Unknown | |
| Helix Tunnel | 0.75D | 1st | Exterior Tunnel | yes | Baked Clay |
| Monolith | 0.75D (Inw to Outw) | 1st | Inner Bridge | no | Rock |
| Spire | 0.25D to 0.75D | 1st | Ladder | no | Crystal |
| Unknown | 0.25D | 2nd | Disk | Titanium | |
| Amberon (perhaps) | 0.25D | 1st | Outer Bridge | Amber | |
| Hyperkone | 0.0D to 0.25D | 1st | Half a Spiral | yes | Diamond (when angular) |
| Amberon (perhaps) | ~0.0D | 1st | Exterior Tunnel | Glass | |
| Visible Light | 0.0D | 0 | EM Spiral | no | - |
| Photosphere | ~-0.0D | -1st | Exterior Tunnel | no | Unknown |
| Amplipole | -0.25D to 0.0D | -1st | Half a Spiral | no | Unknown |
| Corona | -0.75D to -0.25D | -1st | Ladder | no | Unknown |
| Sun Magnetic Field | -1.25D to -0.75D | -1st | Spiral | Unknown |
![]() There is a spiral shaped icon at the top right corner of this page. If you click on it it will open a small window that contains almost the same table as the one shown above. Try to open it for a moment. This is one of those tables that you want to click on every now and then to find the position and dimension level of a specific vortex in the sequence.
There is a spiral shaped icon at the top right corner of this page. If you click on it it will open a small window that contains almost the same table as the one shown above. Try to open it for a moment. This is one of those tables that you want to click on every now and then to find the position and dimension level of a specific vortex in the sequence.
When reading the pages on this website, keep in mind that the word 'vortex' is used in somewhat of a different context than it is used by many other sources. Unlike other descriptions of a vortex, the vortices described on this website do not all have a visible rotational flow, only some. In the infinity-theory, a vortex can be characterized by many shapes of movement, yet it is recognizable and can be reproduced in different environments under similar conditions.
Also keep in mind that some of the things that are going to be discussed on this page are going to be discussed in greater detail on other pages. There are some topics I need to address here briefly to avoid confusion a little later on.
Core and Periphery
A vortex can have a core, a periphery or both a core and a periphery. The core lies at the center of the movement of the vortex and is volume-less and can not be seen. The periphery is the volume around the core, which is in many cases visible, and often its movement can be seen.
If a vortex only has a core then the energy and waves are only electromagnetic. If the vortex has a periphery, then the vortex emits or receives waves of which its type are dependent of the location within the transformation sequence, in particular which half cycle. For instance, if the vortex is located in the first half cycle, then it will emit pressure waves when formed in air, most often in the form of acoustic waves, sound. One of the simplest examples of this is a drum, which creates a bulb vortex. The frequency of the acoustic waves, emitted by the periphery, becomes higher when dimensionality increases and becomes lower when dimensionality decreases. (For instance, this can be influenced by the size of the drum. Larger size is higher dimensional, smaller size is lower dimensional).
If the vortex has both a core and a periphery then the periphery also emits or receives waves, but if the core emits and receives waves as well is something I'm unsure about. And the vortices that appear to have only a periphery might still have a core that is no longer internal but runs outside the body of the vortex. This is also something I'm not sure about yet. If you look at the first half cycle of the sequence for example, then the lowest dimensional vortices (most yang), the disc and spire, only have a core and no periphery. The high dimensional (yin) vortices, the revolute, belt and scroll ring, only have a periphery, thus no core. The vortices in between these, the helicone, swirl and bulb, have both a core and a periphery.
I believe that the core within a vortex that also has a periphery, is an electromagnetic movement along a given path, and only a single line with no volume that can not be detected. But this is quite uncertain. Logic tells us that when we see a periphery that rotates like a helix around an axis, that there must be something at the center of that movement that influences the rotation of the vortex. The periphery however, is physical and is made of matter. These peripheral movements can be seen with the naked eye if the vortex is not too high dimensional. A vortex without a periphery can not exist as matter.
Some high dimensional vortices can still keep on existing when they're cut in half, or when a section of the vortex is cut away from the vortex. This does not seem to be possible with low dimensional vortices. The ability for a vortex to be able to survive as a partial version of itself depends on whether the vortex has a core. A vortex with a core can not be cut in a smaller piece and keep on existing. A vortex without a core can. You will see several examples of this later on with vortices like the scroll ring and the wake belt.

Let us look at a helicone as an example, one of the ladder vortices within the first half cycle of the sequence. A helicone with the minimum number of movements is made of only two movements. There´s one straight core at the center, and there's one movement rotating around the straight core. Other vortices that have a periphery have movements which rotate in two opposite directions simultaneously. These movements are braided. When these movements are braided then the rotation in the movement is no longer visible, because these two opposite movements result in one single movement. Thus while in the helicone the rotational movement is always visible to the eye, in other vortices this movement can not be seen because of the braided pattern. It is only in some cases that we can see this braided pattern in organic matter, and there is at least one phenomena that reveals the existence of these braids. There will be examples later on that demonstrate this.
Sum Movement and Meridians
The movement of the periphery can often be seen with the naked eye. In non-turbulent vortices this appears to be one movement, which can also be an outward or inward movement. What is not obvious when you look at this peripheral movement is that it is often composed of multiple smaller movements added together. The result that we see is called the sum movement. This is all the smaller movements added together that form the peripheral movement. These individual smaller movements are called 'meridians'. These meridians are only revealed to us in organic matter. So far, there hasn't been a way to determine that they exist within inorganic matter.

By looking at growth patterns that can be found in organisms, we can determine that these individual movements are braided. Living organisms are like vortices that are frozen in time. The bark of a tree or the cross-section of animal horns reveals the zigzag pattern that is formed by these individual movements. Only some tree barks show these individual left and right turning movements. But even on a tree where this pattern is not so clearly visible, the path of one of its left or right turning meridians can become visible when lightning strikes the tree.
.jpg) Image by Christopher J.Earle from Gymnosperm Database |
 |
 Image by US Fish and Wildlife Service |
| Helical pattern on a bark | Weave pattern on a bark | Weave pattern in a mammoth tusk |
In all cases when you are looking at the movement of a vortex, then what you'll see is the sum movement. You cannot spot the individual movements with the naked eye. In vortices that appear in fluids you cannot see the braided patterns. We only see the sum movement. It could be perhaps that these individual movements are visible when a fluid or vortex starts to resonate. It could be that that the patterns that appear on a resonating fluid is what reveals to us how the movements are braided.
People who study fluid mechanics and read the pages on this website will probably scratch their head a couple of times when they hear me talk about these individual movements. This is understandable because all they know about is the sum movement and it was unknown until now that this sum movement is made up out of multiple individual movements. It will also take some time for me to convince the science world that these individual movements are really there. The clues are all there, but not everyone will be easily convinced.
Ladders, Spirals, Bridges, Tunnels, Disks and Bells
A vortex class is a collection of vortex types that share some of the same characteristics. Each vortex belongs to one of eight classes. Spiral, ladder, outer bridge, inner bridge, disk, tunnel, bells or suprabells. Each vortex class also forms a morph sequence of its own, where one vortex within the class can change into another subsequent vortex within that same class.
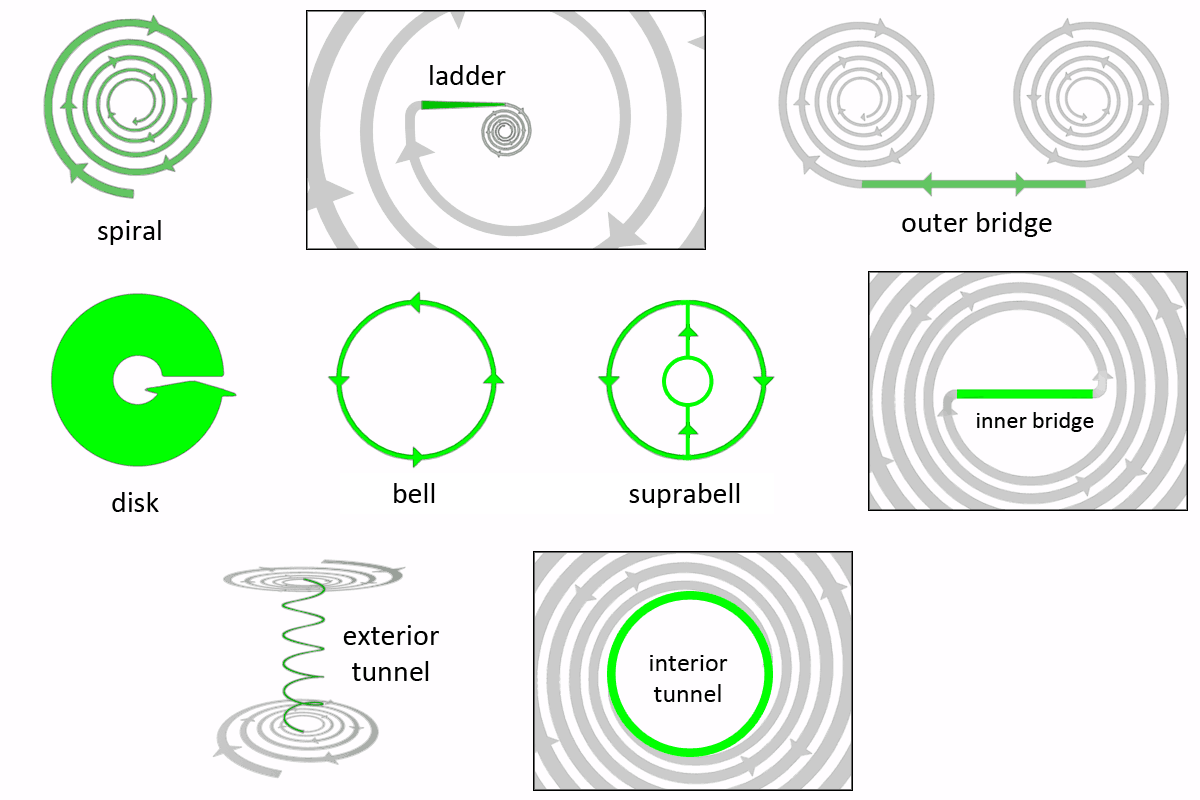
Ladders and spirals are vortices that have two ends each with a different dimensionality. Movement along the path of a spiral or a ladder involves an increase or decrease of one dimension level. Bridges and tunnels are vortices where dimensionality does not increase or decrease, but they have two ends with both a different direction of movement. There's also a class called bells, which are vortices that do not have a start or end but are looping onto itself.
Now think of a ladder that you climb as a vortex where dimensionality increases, and a spiral staircase that you climb as another vortex where dimensionality increases. Then there are bridges that connect either the large end or small end of two spiral staircases representing a vortex in which dimensionality stays the same, but of which both ends lead to two different directions of rotation thus two staircases that rotate in directions opposite of each other. At the bottom of a spiral staircase you will sometimes find a tunnel instead of a ladder or inner bridge. The tunnel will lead to a spiral in which the direction of movement is opposite of the first spiral. Thus outward vs inward or inward vs outward.
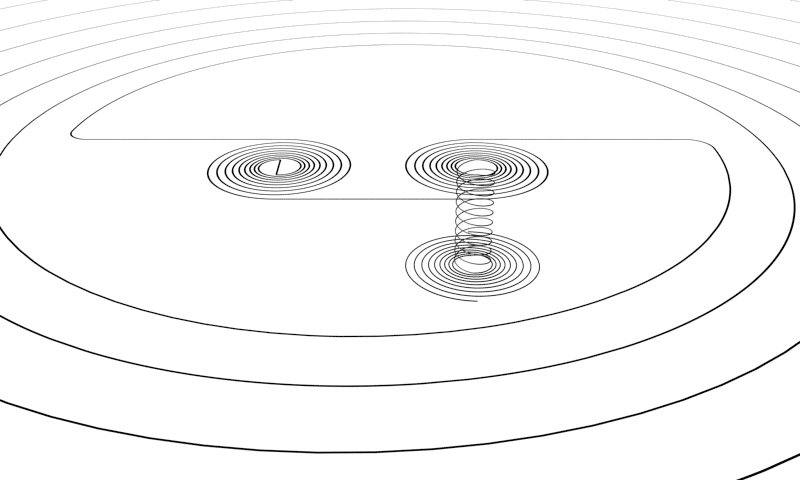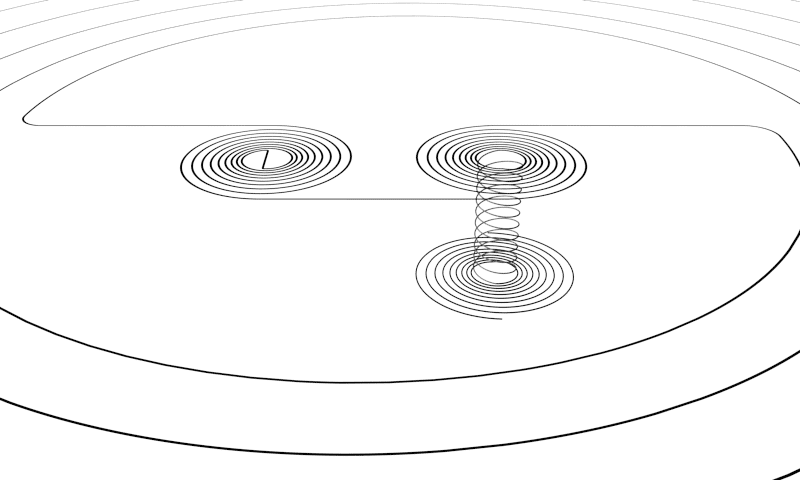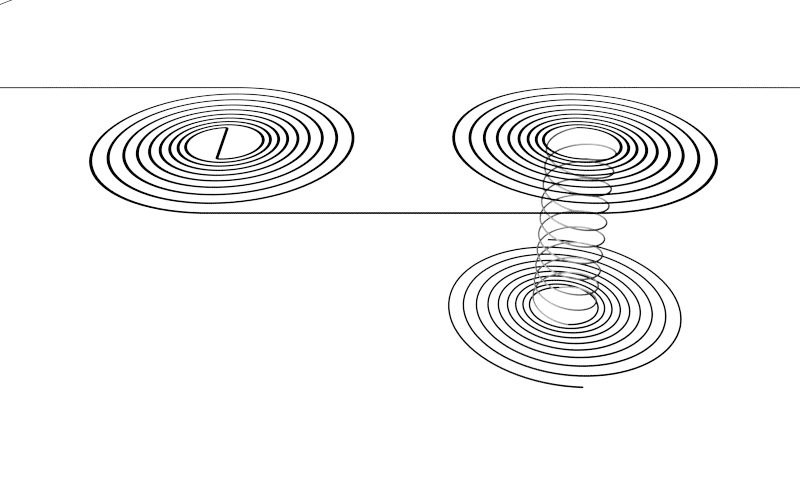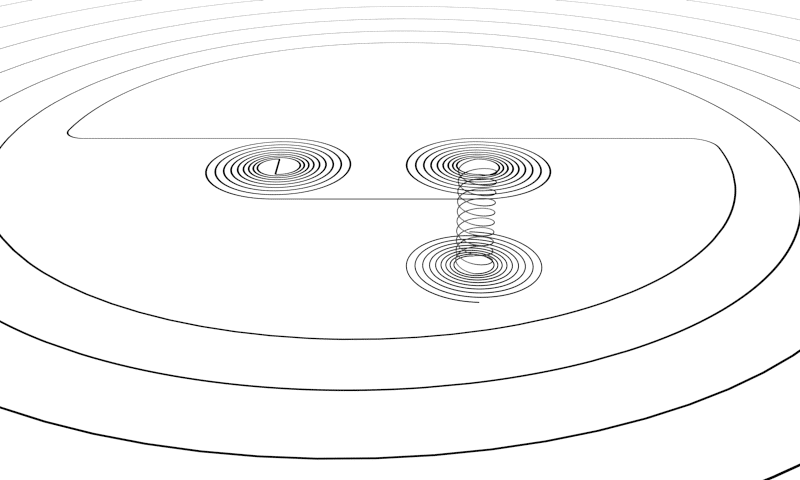
A spiral connects two non-equal ladders (non-equal in dimensionality), a ladder connects two non-equal spirals. A bridge connects the ends of two equal spirals that are mirrored. A tunnel also connects two spirals that are equal but have a different direction of movement.
When you fit these puzzle pieces together to make an entire sequence of the first eleven dimension levels that is fully connected without any gabs, than that movement is mostly dictated by the spirals and the ladders. The order of the sequence is: ladder - spiral - ladder - spiral - ladder - spiral - ladder, and so on. And then in between bridges and tunnels can also connect these vortices. Bells do not seem to connect to other vortices within the sequence, but it could be that there are hidden lines that do connect to other vortices.
Dimension Levels
The definition of a dimension level is determined by the spirals and the ladders. These vortices have a different dimensionality at both ends, so the dimensionality of the vortex alters over a range of dimensions. This range for both ladders and spirals is 0.5D, in simple terms this means that:
one dimension level = ∆0.5D
and
two dimension levels = ∆1.0D = one axis
and
one ladder + one spiral = one axis
and
2D + one ladder + one spiral = 3D
Needless to say, everything that we see is 3D, we humans are made to see in only three dimensions, because our eyes project everything to three dimensions. But that what is projected is in most cases not perfectly 3D. Only the vortices that lie on the central balance points are 3D in both our human perception and in the number of dimensions that are being projected.
On each dimension level within the first forward half cycle lies either one ladder or one spiral. You should remember that one dimension level is a range of 0.5D, thus half an axis. Two of these dimension levels, thus one ladder plus one spiral forms one axis. Why this is so is not certain at the moment. It could be because each of these vortices belongs to one of two possible directions of movement on this axis, or it could be that one vortex incorporates the movement along the axis (the ladder) and the other incorporates the rotation around this axis (the spiral).
Low End and High End of Vortices
When I mention the low end of a vortex, I refer to the lowest dimensional end of that vortex. And the high end is used to refer to the highest dimensional end of a vortex. This only applies to ladders and spirals, not for vortices that have two ends with an equal dimensionality level. This term is not used for bridges, tunnels or bells.
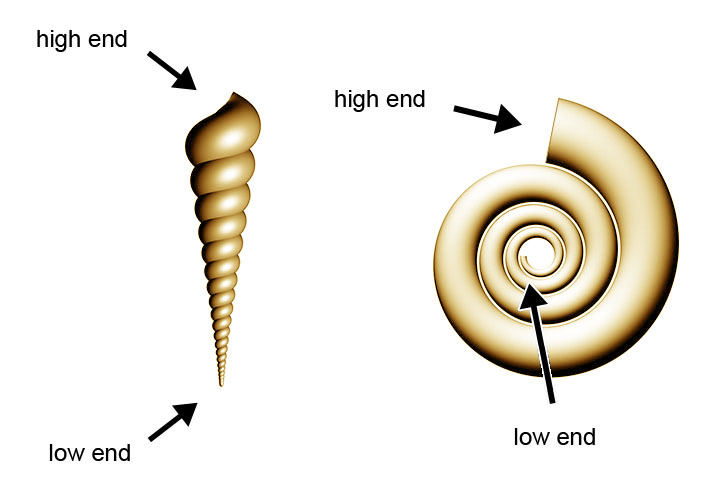
You have to stay alert when this term is used for spirals. In the lower two spirals, the disc and the swirl, its centers are the low ends and the outer part is the high end. But in the other two spirals this is reversed, the inner part of the spirals are the high ends and the outer parts the low end. This is quite obvious if you think about it but you´ll be tricked if you don't pay attention. When you apply this term to ladders you also need to be aware that the larger end of a vortex is not always the high end. It all depends on whether the vortex lies below or above the central balance point.
High and Low Bridges
Besides that a bridge can be either an inner bridge or outer bridge, these bridges can also be grouped into high and low bridges. An inner bridge connects to the smaller inner end of a spiral while an outer bridge connects to the larger outer end of a spiral. A high bridge connects to the highest dimensional end of spiral while a low bridge connects to the lowest dimensional end of a spiral. A high bridge is not always an outer bridge, because the large end of a spiral is not always the highest dimensional part of the spiral. And a low bridge is not always an inner bridge, because the small end of a spiral is not always the lowest dimensional part of the spiral.
All the existing bridges can be grouped into inner and outer bridges, and all existing bridges can be grouped into high and low bridges. High and low bridges are not a new or separate class of vortices. Making inner and outer bridges an official vortex class and not the high and low bridges was a decision I had to make at some point. The other choice could have been favorable as well. But the high and low bridges can still be considered to be a sub-class. One that tells in a different way to which end of the spiral the bridge connects.
Inner End and Outer End of Spirals
The inner end of a spiral is the small end that lies in the center. The outer end of a spiral is the large end that lies furthest away from the center. In some spirals the inner end is the low end of the spiral (like in the swirl, shown below, left) and in other spirals the inner end is the high end of the spiral (like in the revolute, shown below, right). The same holds true for the outer end.
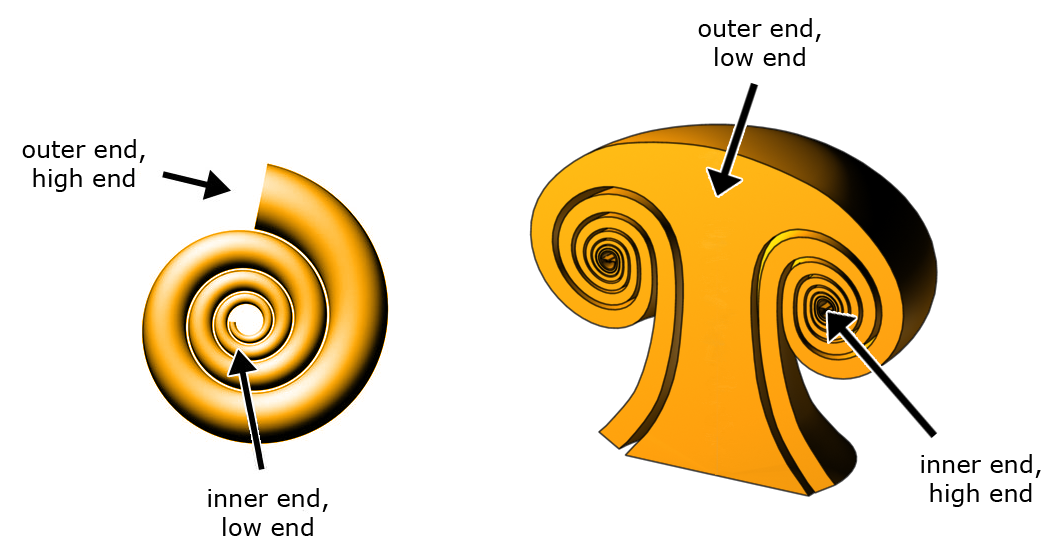
In the upper right picture, the image of the revolute, I've drawn both the revolute and the pylon, which is what looks like the stem of the mushroom and is connected to the revolute. You need to be aware that these are two different vortices, the pylon is a ladder and the revolute is a spiral that starts at the center top of the stem, thus the spiral does not start at the bottom of the stem. The revolute is somewhat easier to visualize when you include the pylon.
Belts

There's also a collection of vortices that are called belts. A belt is not a vortex class but are vortices from different classes. The name for this collection of vortices is derived from the asteroid belts, which have a similar annular shape. Some of these belts look somewhat alike but they are either different in shape or have different paths of movement. The trajectories of their meridians are always unique for each type of belt. Two belts are disks, one belt is an inner bridge, one is a ladder, and one is an outer bridge.
Orbs

And there's another collection of vortices that are called orbs. Orbs are in most situations not that hard to identify because their shape is that of a near perfect sphere. But despite that their shape is always a near perfect sphere they can be different types of vortices and also belong to different classes. So an orb, like a belt, is not a vortex class but a vortex from a collection of vortices from different classes. Some orbs can be be spirals, some orbs are outer bridges, some are tunnels combined with spirals. In the lower dimensions an orb is made up of one vortex type. In the higher dimensions orbs can be made up of more vortex types. Orbs can also be nested into other orbs, as layers. Orbs are always negative dimensional and they sometimes form an entire sequence of orbs. Orbs from a different type can look very much alike in shape, but just as with different types of belts, they have different paths of movement. The trajectories of the meridians are unique for each type of orb.
Spiral Arms
Some spirals are single spirals, other spirals are double spirals. When two spirals form a double spiral than that spiral is still called a 'spiral', it is not called 'two spirals'. Instead, this spiral is called a double spiral with two spiral arms. So these individual spirals that make the whole spiral are now called 'arms'. This is a naming convention which is used throughout this site and is an important one to introduce at the start because otherwise it might be confusing to understand which spiral I'm talking about, the whole spiral or one of the two individual spiral arms.
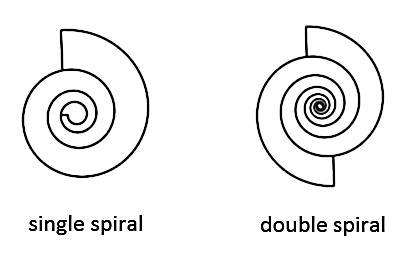
In a swirl spiral or a disc spiral this naming convention is a logical one. In astronomy the words 'spiral arm' are already used for spiral galaxies, which are called 'swirls' in the infinity theory. This naming convention is pretty obvious for swirl spirals or disc spirals. For such spirals, most people already know what is meant when when the words 'spiral arm' are used. But for a revolute spiral or a scroll ring, this naming convention might not be so obvious. In those spirals, the two individual spirals that are nested into each other and make out the larger spiral do not look like arms, but they are still called arms. So be aware of that. It is best to use the same terms for all of the spirals because the characteristics of these phenomena are very much the same.
Turns within the Sequence
There are five locations within the first half cycle of the sequence, at the inner end of the spirals, where the movement makes a 90 degree turn when progressing from spiral to ladder. I'm not sure if the turns belong to the spirals or to the ladders or that they should be classified as separate vortices. The vortex space these turns take into is small compared to the sizes of the adjacent vortices. For now I've decided to keep them unclassified.

Three of these turns have not been observed yet. Only the turn between the swirl and helicone, and the turn between the bulb and the pylon has been observed (second and third from the left in the image above). The others were found by looking at the gaps in the puzzle and determine what piece would be needed to fit there. Logic is what revealed them. It is possible that these turns can also be found within other cycles of the sequence besides the first half cycle. This is a question that still needs to be answered.
The Medium
A vortex of one type can appear in more than one medium. The medium is the substance in which the vortex forms. This can be a liquid, solid, gas or plasma. The type of medium influences how the vortex looks like, both in proportions, and texture/color. In all of the coming pages I drew the vortices in one single color, which is in most cases orange/yellow. This color is unrelated to how the vortex looks like in real life. The images only show the shape of the vortex in its most simplified geometrical form. Color can be diverse depending on the medium.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |



