The Ladders
A ladder connects the high end of one spiral with the low end of another, higher dimensional spiral. The movement from one end of the ladder to the other involves an increase or decrease of one dimension level. Six different ladders have been found within the first forward half cycle. The spire, helicone, amplicone, pylon, aureole belt and the omega ladder. All of them have been confirmed to exist, except one of them, the omega ladder, has not fully been observed. How it has been determined to exist is explained on both this page, and on the page about morphing and shifting.
The basic shape of movement that dominates in all of the ladders is a movement that continuously progresses in a constant direction of one axis or in the direction of two or more axes simultaneously, sometimes combined with a helical movement, but does not involve a spiral-type of movement. Spirals tend to align themselves horizontally under the influence of gravity. But the ladders that move along a single axis tend to align themselves vertical under the influence of gravity.
The sum peripheral movement in a ladder can go from the low end to the high end, or from the high end to the low end, yet I still haven't seen all the ladders move in both directions. In most ladders we see a movement that goes from the low end to the high end. The helicone is one ladder which I've seen move in both directions. It is not fully understood what the conditions are for a ladder to flow in the opposite direction, thus from the high end to the low end.
Keep in mind that in most cases when you encounter a vortex in our physical world, then you only see a single vortex without a connection to a subsequent vortex. Only in some cases these connections are revealed to us. In most real-world examples shown in photographs or videos, you will only see a single ladder. But examples of ladders connected to subsequent vortices will also be shown throughout these pages.
Spire

| Classification | First ladder of the first cycle |
| Dimension | 0.25D to 0.75D (first dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | No |
| Rotational sum movement | No |
| Minimum number of movements | 1 |
| States of equilibrium |
Inorganic: Crystal Organic: Unknown |
| Origin of the name | Spire as in the sharp tip on top of a building, which shape closely resembles this vortex. If you play video games then you might know that in Myst III there is a crystal age named Spire |
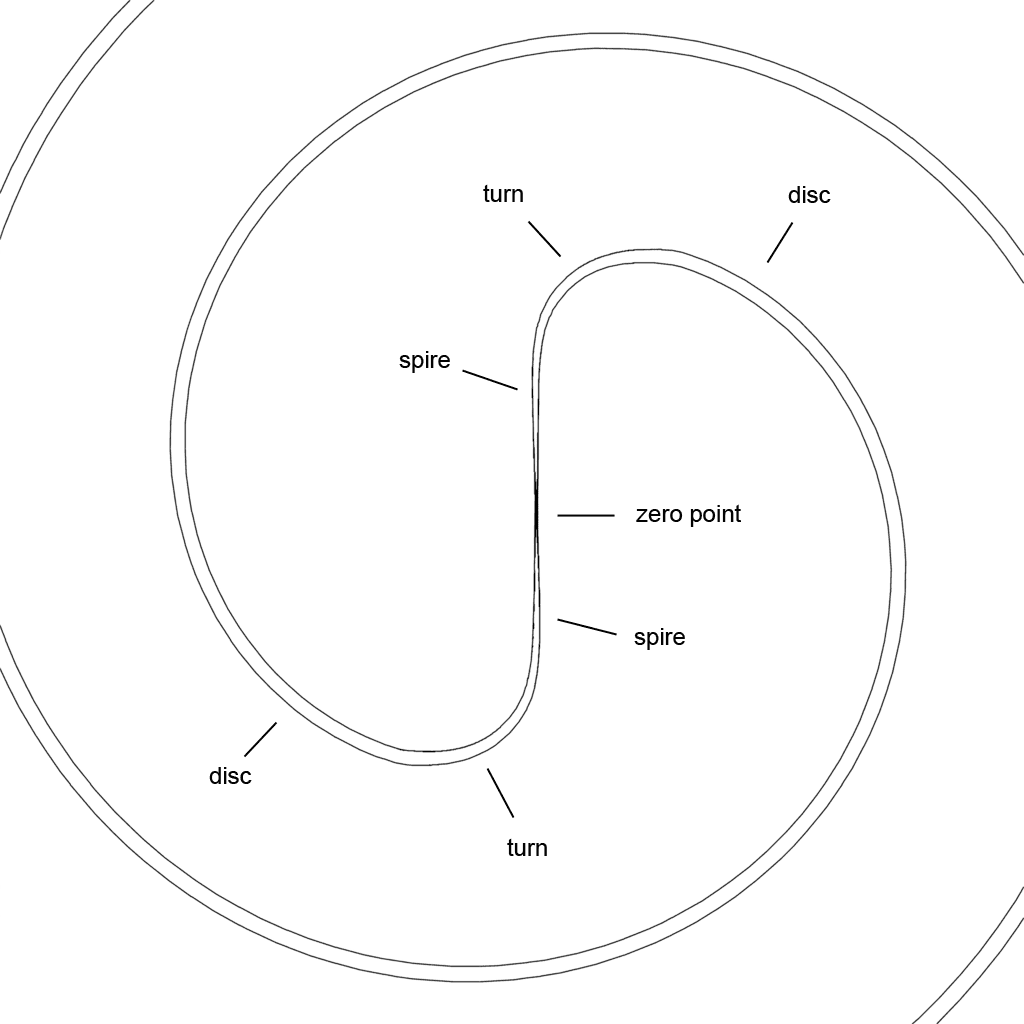
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the first dimension level is called a spire. A spire is nothing more than a single movement in a straight line, with an acceleration in the direction of the low end (and thus a deceleration when the movement goes in the direction towards the high end). The spire is a non-rotational vortex.
Note that the acceleration of the vortex flow is only relative to the size of the diameter of the vortex at the location along its length axis where the speed is measured. The real measured speed is equal at all locations along the length axis. This applies to all ladders and all the spirals as well. With spirals for instance, when you see a vortex flow spiraling inward to the center of the vortex, the speed of flow appears to increase towards that center, because the rotations succeed one another faster and faster. But when the speed is measured at any given location in the spiral those speeds come out as equal everywhere. When a large explosion is viewed from a distance its movement appears to go slower than a smaller explosion that is viewed from a distance. But when we measure the speed of the shock wave then that speed is equal for both explosions. That speed is the speed of sound. The speed that is mentioned here is thus a relative speed, a speed relative to size.
When a spire is unmorphed it does not have a periphery, only a core. This means that the spire can not be visible when it is not morphed. In all the drawings of a spire I deliberately drew a highmorph spire, thus a spire that is partially morphed into a helicone. I choose to illustrate the spire in this way so that you get a better feel of what a spire is, in a more recognizable form, which i think is better than what you would get if I had only shown a straight core line.
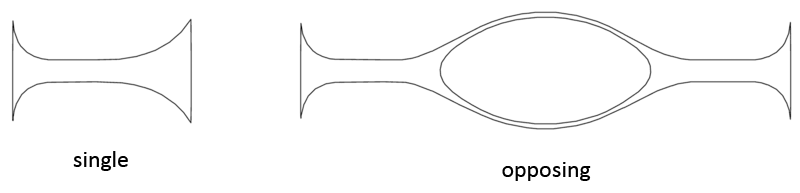
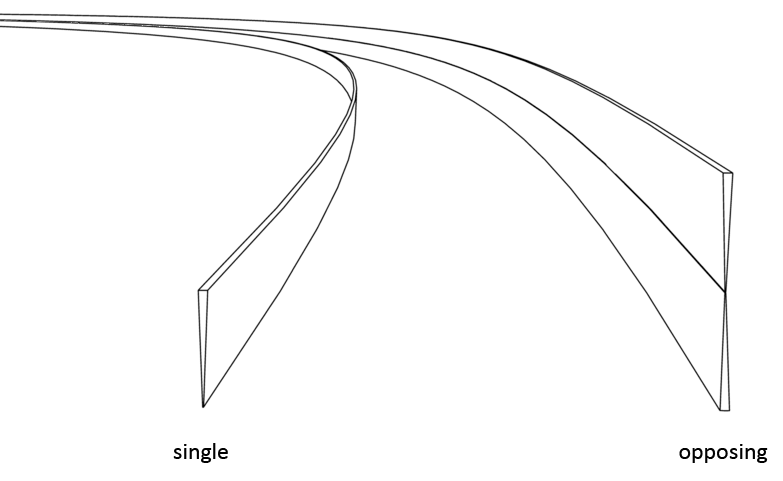
Every ladder in the sequence can be connected to a spiral at its low end and its high end. When a ladder is connected to the inner end of a double spiral, then one ladder connects to one spiral arm, and the other ladder connects to the second spiral arm, and the two ladders are opposing each other with a gab in between. That gab is then filled by a double spiral, or a binary spiral (on all the examples on this page I've used double spirals). This spiral connects these two ladders at their other two ends.
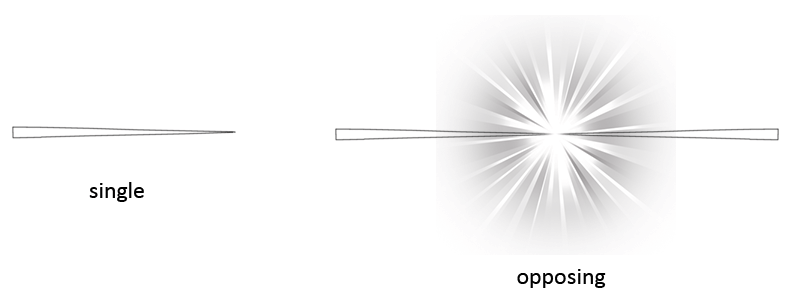
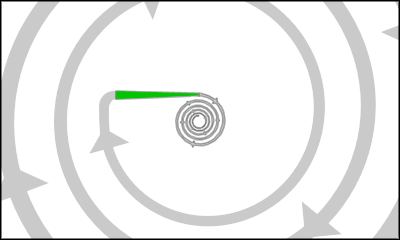
So too can the spire form as part of two opposing ladders. This is what is shown in the illustration above. At the center of the two opposing spires you see a burst of light. In the case of a spire that is what you can expect to find between two spires. Light is actually a spiral too, which will be explained on the page about the EM vortices.
 |
 |
| Image © NRAO/AUI | |
| Single | Opposing |
The spire in the images above is a highmorph spire, thus a spire that is partially morphed into a helicone. Because this spire is a highmorph, it also has a small periphery around it, and so it has a visible shape.
The spire connects to the disc at the high end, and to the zero point at the low end (the zero point is where light comes from). In the image below you again see two opposing spires, and how they connect to the disc when they form a sequence with the disc and other vortices. The spire is the low dimensional antipode of the omega ladder and the double negative antipode of the corona.
Because the shape of a spire is so simple, there are many observations that look like spires. But only some of them probably are. I will mention two of such observations here. These are relativistic jets (macrocyclic) and wingtip vortices that form at high velocity flight (mesocyclic).
Relativistic Jets
AndWFPC2TeamAndNASA_Edited.jpg)
Image credits: HH1/HH2 - J.Hester (ASU),WFPC2 Team, NASA;
Cygnus A - C.Carilli, NRAO. Image was edited with text and arrows
Relativistic jets are extremely powerful jets of plasma which emerge from presumed massive objects at the centers of some active galaxies, notably radio galaxies and quasars. Their lengths can reach several thousand or even hundreds of thousands of light years.
The photo above shows two such jets. These two jets are spires, two ladder vortices. The light source in between them is where the zero point is at. If you look carefully at these jets, you will see that there's a slight helical rotation in them. This is because these jets are highmorph spires, spires that are partially morphed into helicones. When a spire is only a little bit upmorphed then it looks like a sharp needle without a helical rotation in it. When the spire upmorphs a bit more it starts to show a helical rotation.
Still there is some inconsistency here and thus some doubt. The reason that I doubt if these jets really are spires is that some of the relativistic jets appear to be made of plasma, and plasma is something we normally only encounter within the inward dimensions. Although the spire lies very close to the inward dimensions, it still lies one step away from it. And if this spire would be a lowmorph spire, its shape would look different.
Wingtip Vortices during High Velocity Flight

Image by U.S. Air Force, U.S. federal government
Wingtip vortices appear quite often on the tip of the wings of airplanes. When the aircraft flies at high speed then the wingtip vortices that form are spires. When the aircraft flies at lower speed then the wingtip vortices that form are helicones. Fast movement is low dimensional (yang), thus low dimensional vortices form. Slow movement is high dimensional (yin), thus high dimensional vortices form.
Helicone
![]()
| Classification | Second ladder of the first cycle |
| Dimension | 1.25D to 1.75D (third dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | Yes |
| Minimum number of movements | 1 + 1 |
| States of equilibrium |
Inorganic: Marl Organic: Unknown |
| Origin of the name |
Heli because of its rotational helical movement Cone because of its cone shape |
![]() The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the third dimension level is called a helicone. It's shape is a conical helix with a straight core running through. In the image above I deliberately drew a helicone with thick windings. This is only to illustrate its helical shape. In real observations the windings of a helicone are finer and less evident, but the rotation around the core is in most cases detectable if you can observe its movement. The helicone is the second ladder in the sequence, it connects to the disc at the low end and to the swirl at the high end. It is the first vortex in the sequence that has both a core and a peripheral movement even when it is unmorphed. The helicone is the low dimensional antipode of the aureole belt.
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the third dimension level is called a helicone. It's shape is a conical helix with a straight core running through. In the image above I deliberately drew a helicone with thick windings. This is only to illustrate its helical shape. In real observations the windings of a helicone are finer and less evident, but the rotation around the core is in most cases detectable if you can observe its movement. The helicone is the second ladder in the sequence, it connects to the disc at the low end and to the swirl at the high end. It is the first vortex in the sequence that has both a core and a peripheral movement even when it is unmorphed. The helicone is the low dimensional antipode of the aureole belt.
The rotation around the core is always in only one direction and in most cases it is detectable. The helicone is thus a rotational vortex. This makes helicones easy to distinguish and identify. Because the helicone is the first vortex in the sequence with a periphery, it is also the first vortex in the sequence that produces (inaudible) sound (when its medium of existence is air). The disc and spire only have a core movement, thus only produce electromagnetic waves, unless they are highmorphs.
Like any other ladder in the sequence, the helicone can stand opposed to another helicone, by connecting with a double spiral in between. The spiral that connects to the lower end of the helicone is the disc. Below you can see how this combination of vortices looks like.
![]()
For a helicone, the minimum number of meridians is 2, one core movement and one peripheral movement, which rotates around the core. Some examples of helicone vortices are: the bar of a spiral galaxy (macrocyclic), most tornadoes (mesocyclic), wingtip vortices and tornado in a bubble (mesocyclic).
The Bar of a Spiral Galaxy
![]()
Image by NASA/JPL-Caltech, image was edited with text and arrows
Approximately two-thirds of all spiral galaxies contain a central bar-shaped structure. In the center of the bar you will find a smaller spiral. The two straight arms that connect the larger spiral with the smaller spiral are helicones. The above image is a picture of NGC1097. Its shape is a bit disordered but the two bars are clearly visible and you can see these ones are somewhat conical. You can also see the sharp 90 degree turn that the sequence makes from the swirl to the helicone.
Tornadoes

Image by U.S. National Oceanic and Atmospheric
Administration
Tornadoes provide a great deal of information about helicones because the majority of them are helicones. Note that tornadoes often form at the center of hurricanes. A hurricane is formed by the same type of vortex as a spiral galaxy (swirl). When a spiral bar develops it forms a helicone. The same thing happens here on earth when a hurricane becomes strong enough and forms a helicone in its center in the form of a tornado. Except here the tornado is pulled to the ground thus the disc and second helicone never forms. Tornadoes are low dimensional vortices, which is apparent by their characteristics. They are strong, relatively fast and are shaped by simple movement. There's not much freedom of movement inside a tornado, there's more friction, that is why objects in its path are pushed away by the flow of the vortex.
Water Vortices
Water vortices are like tornadoes underwater. To create one all you need to do is pull the plug in your bathtub. A water vortex does look a lot like a helicone but there are two things that conflict with what we know about helicones. Thirst thing is that this vortex is hollow, its an aircore vortex, and a helicone is not. Second thing is that at the top it connects to a whirlpool, which is a swirl. But it connects to the center of the swirl in a very different way that a helicone connects to the center of a swirl.
This vortex is in fact a different type of vortex, of a different class, a so-called tunnel vortex. What a tunnel vortex is will all be explained on the page about the tunnels.
 Image by Robert D Anderson, under CC BY-SA 3.0 license |
 |
Wingtip Vortices at Low Velocity Flight
Wingtip vortices that form at low velocities are helicones. At higher velocities the wingtip vortices become spires. If there is a rotational movement in the wingtip vortex then you know that it is a helicone. Not always are these vortices visible to the naked eye. Below is a video that shows a method of detecting the rotational movement in these wingtip vortices.
One characteristic that low dimensional vortices share is their short lifespan. They disappear quickly unless there's a force that keeps them flowing. When there are white trails visible behind an aircraft that stay in the air for a long time then they're not helicones or spires but some other vortices. These could for example be contrails, which are scrolls, a spiral vortex higher in the sequence. Sometimes you can see both contrails and wingtip vortices behind one airplane. The scrolls can form around the spire, thus with a spire at its center axis.
Tornado in a Soap Bubble
This is a nice one. See how this person makes a tornado inside a soap bubble. Neat trick, well performed. This is the same vortex as a tornado over land, except much smaller and upside-down.
 |
Amplicone
![]()
| Classification | Third ladder of the first cycle |
| Dimension | 2.25D to 2.75D (fifth dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 1 + 4 (estimate) |
| States of equilibrium |
Inorganic: Dust Organic: Unknown |
| Origin of the name | Ampli as in 'amplify', refering to its progressive increase in width along its axis. These first 5 letters are also used for the amplipole. Cone because of its cone shape |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the fifth dimension level is called the amplicone. The amplicone is the third ladder in the sequence and connects to the swirl at the low end and to the bulb at the high end.
Just as with the other ladders, two amplicones can connect in a way that they stand opposing to each other, in this case when connected with a double swirl. The image below shows how these opposing ladders looks like.
![]()
While most vortices are visible in outer space, and their shapes can be identified in various large objects that can be observed in space telescope images, the amplicone is most often not visible. Its location can be determined by finding a swirl that lies close to a bulb, an amplicone should connect these two in between, but the vortex itself remains in most cases (but not all) invisible. It is not clear why most amplicones are not visible in space, the vortex itself is not that high dimensional, and it does have a peripheral movement, so one would expect it to be visible.
Just like a helicone, the amplicone has a conical shape. But in its appearance there are two major differences when compared with a helicone. A helicone is straight, while the amplicone is curved, its thickness does not increase linearly but exponentially (ampli means increase). A helicone also has a rotation in a single direction around its directional axis, left or right depending on whether the vortex is left or right-turning. An amplicone does not show a rotation around its directional axis, nor seems there to be a movement in the direction of the axis, or only a slow movement. This is because the amplicone's left and right turning meridians, which are braided, are almost or completely horizontal and forms a sum movement that cancels each other out. For this reason the amplicone is known to be a non-rotational vortex.

To understand the logic of the direction of movement of the amplicone you need to look at the other ladders. The spire has only a straight movement along its axis, when it morphs to a helicone the angle becomes tilted, and the flow of the vortex begins to form a rotation. Then when the vortex morphs further the angle becomes close to zero.
I'm not sure if the angle of movement of an unmorphed helicone is 45 degrees. It could be somewhere around 30 degrees. In that case the amplicone probably does have a slow upwards movement along its axis. After the amplicone the movement suddenly changes back to 90 degrees. This is because it morphs past the central balance point, the location of the bulb, which is transition point. Whenever movement passes a that point, the movement changes into a perpendicular direction.
The amplicone has a completely or almost horizontal sum movement at its high end, and thus little or no upwards flow at that high end. But at the low end of the amplicone the upflow is significantly larger, which becomes progressively smaller as the peripheral movement flows from the low end to the high end.
The amplicone is the low dimensional antipode of the pylon. The amplicone is also the first vortex in the sequence that produces audible sound (when its medium is air). Some examples of amplicones are: some tornadoes (mesocyclic), the flow of water past a metal sphere (mesocyclic), the spiral arms in NGC 1365 (macrocyclic).
Tornadoes
 |
 |
Most tornadoes are helicones. But the helicone is a vortex that can morph into an amplicone. This is because the helicone and amplicone are subsequent ladders. One ladder in the sequence can morph into the next ladder. When a tornado is partially morphed into an amplicone, then its rotational movement is slower and weaker then it would be when the vortex was an unmorphed helicone. The vortex is also wider, and grows exponentially at the top.
Flow of Water past a Metal Sphere
When water flows past a metal sphere, then the water that flows away from the sphere forms an amplicone. A metal sphere is of course not a vortex, it is not a bulb. But it has the shape close to that of a bulb, for this reason the water that flows past the sphere connects to it as if it would connect to a bulb. One other such example is when we let water flow past a cone shaped object, that will produce a disc spiral. And another such example is when we let water flow past a disc shaped object, that will produce a helicone/helibar. Those examples will be shown later on.
_FromAnAlbumOfFluidMotion.gif)
Sphere at R = 25.5. Although it is not obvious, the flow is believed just to have separated at the rear at this Reynolds number, in contrast to the unseparated flow of figure 27. Aluminum dust is illuminated in water. Taneda 1956b [image and text taken from An Album of Fluid Motion by Milton van Dyke. Image was converted to GIF and text and lines added].
The spiral arms in NGC 1365

Image by European Southern Observatory (ESO), under CC BY 3.0 license
Image was edited with text and arrows
This is a picture of NGC 1365, also known as the Great Barred Spiral Galaxy. Here, the shape of the helicones is more prominently visible. But their width grows more exponentially, while a helibar should have linear growth. This is because these helicones have partially morphed into amplicones, which is the next ladder in the sequence.
Pylon

| Classification | Fourth ladder of the first cycle |
| Dimension | 3.25D to 3.75D (seventh dimension level) |
| Positive / Negative | Positive |
| Core | Yes |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 1 + 12 (estimate) |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | Pylon because the shape is almost like an upside down road pylon. The vortex also is linked to the buildup of an electrical discharge, hence an electricity pylon |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the seventh dimension level is called the pylon. The pylon is the fourth ladder in the sequence and connects to the bulb at the low end and to the revolute at the high end. The pylon is the high dimensional antipode of the amplicone. The sum movement at the low end flows along the path of one axis towards the high end. Then close to the high end the movement makes a turn sideways in all horizontal directions. In some cases the pylon can be quite long. The pylon is a non-rotational vortex.
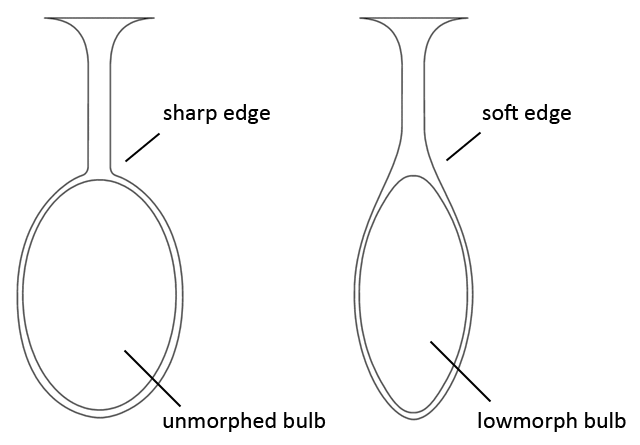
Just as with any other ladder, the pylon can connect to a double spiral that has another pylon connected to the other spiral arm, so that both pylons stand opposing each other. In this case, that spiral is the double bulb (the bulb is the spiral that at first glance does not look like a spiral). The bulb is a vortex that lies exactly on the central balance point and is discussed on the next page.
It makes quite a significant difference if the pylon connects to an unmorphed bulb or a lowmorph bulb. When the pylon connects to an unmorphed bulb then it connects with a sharp edge that makes a large angle. When the pylon connects to a lowmorph bulb it connects with a soft edge that makes a small angle.
Three examples of a pylon are: fluid ejected from a nozzle (mesocyclic), plunger retracted from water (mesocyclic) and falling water jet which dissolves in droplets (mesocyclic).
Fluid Ejected from a Nozzle
Below are two photographs of a dyed fluid ejected through an orifice. The first part of this vortex, the stem of the mushroom, is a pylon vortex, thus a ladder. The next part is a revolute, which is a high dimensional spiral. The revolute is the vortex that connects to the high end of a pylon.

Vortex rings can be formed by sudden ejection of fluid from a tube or orifice. During ejection, the jet rolls up into a toroidal spiral (ring) and in the process, pushes some of the ambient fluid into the spiral. This process is easily visualized by coloring the fluid in the tube with a fluorescent dye and illuminating it with a laser sheet (known as planar laser induced fluorescence or PLIF) to obtain a cross-section of the flow [images and text by A.B. Olcay, and P.S. Krueger. Two images were combined into one GIF and yellow markings added].
Plunger Retracted from Water
The video above shows a pylon that forms underneath a plunger when retracted from water. The device used is called a Filament Stretching Rheometer, which can move at very high speeds by using magnets instead of mechanical gears to generate motion. This video, made by Pedro M. Reis, Sunghwan Jung, Jeffrey M. Aristoff and Roman Stocker, was filmed with a high speed camera at 1.000 frames per second.
Falling Water Jet which Dissolves in Droplets
This photo is from Zumthie from Wikipedia. A falling water jet dissolving into droplets. The vortex is an example of both a lowmorph bulb (spiral) and a lowmorph revolute (spiral), connected with a pylon (ladder) and an exobar (outer bridge). The revolute is very lowmorph. It is actually more of a highmorph bulb than a lowmorph revolute because it has not formed spiral arms yet.
Aureole Belt
| Classification | Fifth ladder of the first cycle |
| Dimension | 4.25D to 4.75D (ninth dimension level) |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Rotational sum movement | No |
| Minimum number of movements | 34 (estimate) |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | Aureole because the vortex has the same shape as a person's aureole (aura) is portrayed in illustrations. Belt because it has the same annular shape as an asteroid belt or the Kuiper belt |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the ninth positive dimension level is called the aureole belt. Its appearance is something close to a large, almost flat ring. Its cross-section is slightly tapered, thus one end is thicker than the other end. In mathematics, the overall shape of the aureole belt is called an annulus (if you disregard the tapering). The aureole belt connects to the revolute at the low end, and to the scroll ring at the high end. The aureole belt is circular in shape but its sum movement is not circular, the aureole belt is a non-rotational vortex.
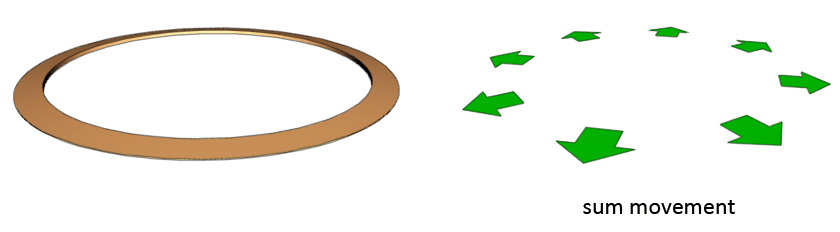
Initially I did not find this vortex through observation but by logical thinking. We know how the helicone connects to the disc and swirl. This vortex should be the high dimensional antipode of the helicone. One lies three dimensions above the central balance point (yin), the other lies three dimensions below the central balance point (yang). But here its shape is not linear but circular. What we get when we put these clues together is a flat ring with possibly a triangular cross-section.
The sum movement is illustrated in the first image with green arrows and is suppose to indicate a flow movement. The arrows to not indicate that the vortex is growing. The aureole belt can grow however, when it morphs into a an omega ladder, such morphing is a different kind of movement then the normal flow movement of a vortex.
The image below shows how the aureole belt looks like deep within the revolute when it connects in a sequence (image is a cut-view of the inner windings of the revolute).
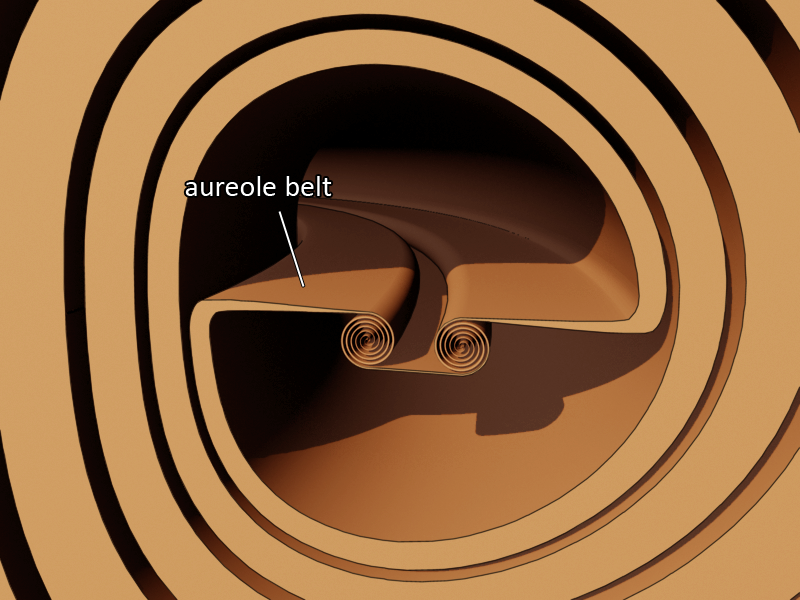
The above image is how the revolute, aureole belt and scroll rings look like in a full transformation sequence, but while most of the vortex connections in the sequence have been observed, this one has not. We have never seen an aureole belt inside a revolute. Anyone who has studied vortex rings and sees the image above will scratch his head the first time seeing this. But if you read all the pages on this website, then slowly bit by bit you will start to understand the logic as to why this setup is to be expected and that one day we should be able to find this. The reason for this is that this setup is the logical continuation of the rest of the sequence, with a 90 degree turn, followed by a ladder and then followed by a spiral. There are many other clues spread out over this website that reveal that the aureole belt and scroll ring are likely to be the two vortices that come after the revolute.
It is not clear whether the low end of the aureole belt is connected at the small radius or at the large radius of the revolute. So it is not clear whether an expansive movement in an aureole belt goes from the small radius to the large radius or the other way around. In the image above I chose the small radius as the low end of the aureole belt.
There are several vortices that have an annular shape, and thus also several observations of belt-shaped vortices. But only one so far is likely to be an aureole belt, and those are the condensation rings which we see around some nuclear detonations (mesocyclic).
Condensation Rings

Some nuclear detonations produce circular vapor clouds. The number of these clouds differs for every detonation. Some have none, some have one, others have multiple rings. These clouds are belts, but not all of them are aureole belts. Sometimes the rings around a nuclear mushroom cloud are aureole belts and sometimes they are laminar belts (see page about inner bridges), and some nuclear detonations even show both types of belts simultaneously. How one is able to see which one is which is by its proportions. Laminar belts are twice as wide measured from inner radius to outer radius as aureole belts. The reason why they are seen here around a revolute (mushroom cloud = revolute) is not completely understood. It is expected that they're supposed to appear inside the revolute, not outside.
When both types of belts appear simultaneously, then the aureole belts are always located above the laminar belts. This is because aureole belts are higher dimensional than laminar belts, thus they appear higher in the sky where the air is higher dimensional than the air at lower altitudes.
 |
Above you see a picture and a video of an aureole belt appearing at the British nuclear detonation named Grapple-Y. It is almost certain that this belt is an aureole belt because it is morphing into an omega ladder, which is the next ladder in the sequence.
Omega Ladder

| Classification | Sixth ladder of the first cycle |
| Dimension | 5.25D to 5.75D (eleventh dimension level) |
| Positive / Negative | Positive |
| Core | No |
| Periphery | Yes |
| Minimum number of movements | 89 (estimate) |
| States of equilibrium |
Inorganic: Unknown Organic: Unknown |
| Origin of the name | The greek letter Omega means 'great O', refering to it being one of the highest dimensional vortices in the first cycle and its ring shape. Ladder because this vortex is a ladder type vortex |
The vortex that reveals the presence of a wave that is the result of an alteration in dimensionality within the range of the eleventh dimension level is called the omega ladder. The omega ladder is the highest positive dimensional ladder in the sequence, and the only one that has never been fully observed. It is the vortex that connects to the scroll ring at the low end and to the infinity ring at the high end (this is not completely correct, there should still be half a spiral in between the infinity ring and the scroll ring, but that vortex hasn't been found yet).
Its shape is that of a very short hollow cylinder / tube. When connected in a sequence it lies at the very center of a scroll ring. The tube is so short that it looks like a ring. There are several ring shaped vortices within the sequence, but this is the thinnest, and the smallest in volume. The illustrations below shows the omega ladder as an extruded circular version of the spire, but its exact shape is still not certain and thus still can only be based on the logic found in the continuity of the sequence. All I know for sure is that it's circular.
The omega ladder requires the highest number of meridians of all vortices in the first half-cycle. Just as with the other highest dimensional vortices in the same part of the sequence, the path of these movements is still unknown. The sum of these movements does not flow in a circular path as the shape of the vortex might suggest, the omega ladder is a non-rotational vortex. The omega ladder is the high dimensional antipode of the spire and probably the positive dimensional antipode of an orb.
Below is a cut-through model image that shows where the omega ladder is positioned deep within a scroll ring when it is connected in a sequence. The illustration looks similar to the illustration of the spire at the center of a disc spire which you've seen at the top of this page. The scroll ring and omega ladder is like an extruded circular version of the disc and the spire. The omega ladder lies at the very center of the spiral and is nothing more than a very thin short tube. The reason why I know that its shape is that of a tube and not annular like the belt is explained on the page about morphing and shifting. The image below actually shows two omega ladders, one below the infinity ring and one above.

Two examples of an omega ladder are ring formations at Grapple-Y nuclear test, and circular cloud formations.
Grapple-Y Ring Formations

I've already mentioned that the aureole belt that appears at Grapple-Y, the British nuclear detonation, is morphing into an omega ladder. This is the only observation of an omega ladder that is almost certain. The omega ladder is higher dimensional than the aureole belt, thus less visible. When morphing from aureole belt to omega ladder the vortex fades out and that makes the omega ladder difficult to observe.
Circular Clouds
 |
 |
This observation is still uncertain, but it is the only other observation that has a good possibility of being an omega ladder. Above you see two pictures taken from two rare circular cloud formations. There's a possibility that these vortices are lowmorph omega ladders, thus vortices that are not completely omega ladders but a morphology between an omega ladder and an aureole belt. Thus almost omega ladders.
There's no full observation of an omega ladder. The aureole belt morphing into an omega ladder at Grapple-Y quickly fades away, and any other observation with such a high probability of actually being an omega ladder is still missing. One of the reasons why an omega ladder has not been observed yet is that the more higher dimensional a vortex is, the more difficult it is to see it with the naked eye (one such example is outer space, where the high dimensional vortices like the belts and scroll rings are even harder to spot than here on earth, because those vortices in outer space are much larger, thus even more high dimensional). No existing phenomenon has been 100% confirmed to be an omega ladder, but it is the logical order of the sequence that tells us there should be one such vortex. Three ladders above the central balance point, and three ladders above the central balance point. The omega ladder should be the high dimensional antipode of the spire. Because of the existence of the spire, it is very likely that the omega ladder exists as well.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |




_PublicDomain.jpg)